Giải bài 47 tr 95 sách BT Toán lớp 8 Tập 2
Trên hình 33 hãy chỉ ra các tam giác đồng dạng. Viết các cặp tam giác đồng dạng theo thứ tự các đỉnh tương ứng và giải thích vì sao chúng đồng dạng.
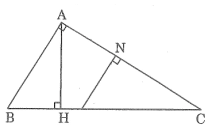
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
- Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
- Hai góc cùng phụ với một góc thứ ba thì bằng nhau.
Lời giải chi tiết
+) \(∆ ABC \backsim ∆ HBA\) vì hai tam giác vuông có góc nhọn ở đỉnh \(B\) chung.
+) \( ∆ ABC \backsim ∆ HAC\) vì hai tam giác vuông có góc nhọn ở đỉnh \(C\) chung.
+) \(∆ ABC \backsim ∆ NMC\) vì hai tam giác vuông có góc nhọn ở đỉnh \(C\) chung.
+) \(∆ HAC \backsim ∆ NMC\) vì hai tam giác vuông có góc nhọn ở đỉnh \(C\) chung.
+) \(∆ HAC \backsim ∆ HBA\) vì hai tam giác vuông có góc nhọn \(\widehat {HBA} = \widehat {HAC}\) (cùng phụ với \(\widehat {BAH}\))
+) \(∆ HAB \backsim ∆ NCM\) vì hai tam giác vuông có góc nhọn \(\widehat {HAB} = \widehat {NCM}\) (cùng phụ với \(\widehat {CAH}\)).
-- Mod Toán 8 HỌC247
-


Cho tam giác ABC vuông tại A (AC > AB ) , đường cao AH . Biết BC= 5 cm , BC= 0.125 cm , M là trung điểm BC , đường trung trực BC cắt AC tại D.
a) Tính AB , AH .
b) Tính tỉ số diện tích của tam giác DMC và tam giác ABC
Theo dõi (0) 0 Trả lời -


Cho tam giác MNP vuông tại M, đường cao MH
bởi Dương Nhựt Thanh Trúc
 19/12/2018
19/12/2018
Cho tam giác MNP vuông tại M, đường cao MH . Gọi D, E lần lượt là chân các đường vuông góc hạ từ H xuống MN và MP.
a) CM tứ giác MDHE là hình chữ nhật
b) Gọi A là trung điểm của HP chứng minh tam giác DEA vuông
c) Tam giác MNP cần có thêm điều kiện gì để DE=2EA
Theo dõi (0) 3 Trả lời -


Cho tam giác ABC vuông tại A , BC=2AB=2a
bởi Quốc Huy
 12/12/2018
12/12/2018
Cho tam giác ABC vuông tại A , BC=2AB=2a . Ở ngoài tam giác ABC , vẽ hình vuông BCDE , tam giác đều ABF và tam giác đều ACG .
a) Tính góc B , góc C , cạnh AB và diện tích tam giác ABC .
b) Chứng minh : FA vuông góc DE . Tính diện tích tam giác FAG , diện tích tam giác FBE .
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC cân, đường cao AH, I là trung điểm AH, N là trung điểm AB, E là giao điểm của CI và HN Chứng minh: a) AE song song HC , b) AEBH là hình bình hành c) F là điểm đối xứng với E qua A chúnng minh B, I, F thẳng hàng.
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC vuông tại A.Điểm D thuộc cạnh BC
bởi Lương Thùy Linh
 07/12/2018
07/12/2018
Cho tam giác ABC vuông tại A.Điểm D thuộc cạnh BC.Kẻ DM vuông góc AB,kẻ DN vuông góc AC;AH vuông góc BC
a,Chứng minh:AD=MN
b,Tính góc MHN
c,Điểm D ở vị trí nào trên BC thì MN có độ dài nhỏ nhất?
Theo dõi (1) 2 Trả lời -


Cho tam giác ABC cân tại A, AM là đường trung tuyến
bởi Mai Linh
 19/10/2018
19/10/2018
Cho tam giác ABC cân tại A, AM là đường trung tuyến. Gọi D là trung điểm của AC. Lấy N đối xứng với M qua D.
a, Tứ giác AMCN là hình gì ? Chứng minh ?
b, Chứng minh tứ giác ABMN là hình bình hành ?
c, Biết AB = 5cm, BC = 6cm. Tính diện tích tứ giác AMCN.
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC vuông tại A có AB = 3cm, AC = 4cm
bởi Mai Linh
 19/10/2018
19/10/2018
Cho tam giác ABC vuông tại A có AB = 3cm, AC = 4cm. Gọi M là trung điểm BC, qua M vẽ MD vuông góc với AB và ME vuông góc với AC (D ∈ AB, E ∈ AC)
a, Tứ giác ADME là hình gì ? Vì sao ?
b, Tính diện tích tam giác ABC và diện tích tứ giác ADME
c, Gọi F là điểm đối xứng của M qua E, đường thẳng BE cắt FC tại K. Chứng minh: FC = 3 . FK
Theo dõi (0) 0 Trả lời -


Tam giác ABC có AB=8cm, AC=15cm, BC=17cm, đương cao AH. Tính độ dài AH
Theo dõi (0) 1 Trả lời






