Giải bài 46 tr 95 sách BT Toán lớp 8 Tập 2
Cho tam giác ABC vuông tại A, AC = 4cm, BC = 6cm. Kẻ tia Cx vuông góc với BC (tia Cx và điểm A khác phía so với đường thẳng BC).Lấy trên tia Cx điểm D sao cho BD = 9cm (h.32)
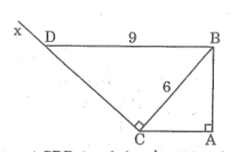
Chứng minh rằng BD // AC.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Lời giải chi tiết
\(\displaystyle {{AC} \over {CB}} = {4 \over 6} = {2 \over 3}\)
\(\displaystyle{{CB} \over {BD}} = {6 \over 9} = {2 \over 3}\)
\( \Rightarrow \displaystyle{{AC} \over {CB}} = {{CB} \over {BD}}\)
Xét hai tam giác vuông \(ABC\) và \(CDB\) có:
\(\widehat {BAC} = \widehat {DCB} = 90^\circ \)
\( \displaystyle {{AC} \over {CB}} = {{CB} \over {BD}}\) (chứng minh trên)
\( \Rightarrow ∆ ABC \backsim ∆ CDB\) (cạnh huyền và cạnh góc vuông tỉ lệ).
\( \Rightarrow \widehat {ACB} = \widehat {CBD}\)
Mà \(\widehat {ACB} \) và \( \widehat {CBD}\) ở vị trí so le trong nên \(AC // BD \).
-- Mod Toán 8 HỌC247
-


Chứng minh ∆DBA ∆ABC và suy ra AB^2 = BC.BD biết ∆ABC vuông tại A có AB < AC và AD là đường cao
bởi Đoàn Thư
 29/04/2020
Bài 4: Cho ∆ABC vuông tại A có AB < AC và AD là đường cao. a) Chứng minh ∆DBA ∆ABC và suy ra AB2 = BC.BD. b) Đường phân giác góc BAC cắt BC tại M, kẻ ME vuông góc với AB (E Î AB). Chứng minh BE.BA = BD.BM. c) ChứngminhDElàphângiácgócADB.Theo dõi (0) 0 Trả lời
29/04/2020
Bài 4: Cho ∆ABC vuông tại A có AB < AC và AD là đường cao. a) Chứng minh ∆DBA ∆ABC và suy ra AB2 = BC.BD. b) Đường phân giác góc BAC cắt BC tại M, kẻ ME vuông góc với AB (E Î AB). Chứng minh BE.BA = BD.BM. c) ChứngminhDElàphângiácgócADB.Theo dõi (0) 0 Trả lời -


Chứng minh tam giác ABE đồng dạng với tam giác ACF biết giác ABC có tia phân giác AD cắt BC tại D
bởi Nguyệt Minh
 22/04/2020
22/04/2020
Cho tam giác ABC, tia phân giác AD cắt BC tại D. Gọi E, F lần lượt là hình chiếu của B và C lên AD
Chứng minh: a, Tam giác ABE đồng dạng với tam giác ACF
b, AE.DF = AF.DE
Theo dõi (0) 2 Trả lời -

 Cho tam giác ABC có BCA=2CBA. M là điểm nằm trong tam giác ABC sao cho MA=CA, MB=MC. Chứng minh rằng BAM=1/3BACTheo dõi (1) 0 Trả lời
Cho tam giác ABC có BCA=2CBA. M là điểm nằm trong tam giác ABC sao cho MA=CA, MB=MC. Chứng minh rằng BAM=1/3BACTheo dõi (1) 0 Trả lời -


Nêu tên các tam giác đồng dạng?
bởi Huỳnh Linh Đan
 11/04/2020
Giúp mình với ạ mình đang cần gấp
11/04/2020
Giúp mình với ạ mình đang cần gấp Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính độ dài các đoạn EC, DA, DB, FA và FC biết tam giác ABC vuông ở A có AB = 15cm, AC = 20cm
bởi Nhóc's Hải
 08/04/2020
Bài 2. Cho tam giác ABC vuông ở A có AB = 15cm, AC = 20cm. Lấy điểm E nằm trên cạnh BC sao cho EB = 5cm. Từ điểm E kẻ ED và EF lần lượt vuông góc với AB và AC (D AB và F AC).Tính độ dài các đoạn EC, DA, DB, FA và FCTheo dõi (1) 0 Trả lời
08/04/2020
Bài 2. Cho tam giác ABC vuông ở A có AB = 15cm, AC = 20cm. Lấy điểm E nằm trên cạnh BC sao cho EB = 5cm. Từ điểm E kẻ ED và EF lần lượt vuông góc với AB và AC (D AB và F AC).Tính độ dài các đoạn EC, DA, DB, FA và FCTheo dõi (1) 0 Trả lời -


cho hình bình hành ABCD, góc A tù, AK vuông góc với BC, AH vuông góc với CD.
Chứng minh tam giác ABC đồng dạng với tam giác AHK?
Theo dõi (0) 0 Trả lời -

 cho tam giác ABC cân tại A, đường cao AD, gọi K là trung điểm AD. Gọi I là hình chiếu của D trên CK . CMR: góc AIB=90 độ
cho tam giác ABC cân tại A, đường cao AD, gọi K là trung điểm AD. Gọi I là hình chiếu của D trên CK . CMR: góc AIB=90 độ Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm. Đường cao AH và phân giác BD cắt nhau tại I.
bởi Lê Ngọc Anh
 01/05/2019
01/05/2019
Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm. Đường cao AH và phân giác BD cắt nhau tại I.
a, Tính AD, DC?
b, Chứng minh: tam giác ABC đồng dạng với tam giác HBA.
c, Chứng minh: AB^2= BH.BC.
d, Chứng minh: tam giác ABI đồng dạng với tam giác CBD.
e, Chứng minh: IH/IA=AD/DC
Theo dõi (1) 2 Trả lời





