Giải bài 31 tr 23 sách GK Toán 8 Tập 2
Giải các phương trình:
a) \(\frac{1}{x-1}-\frac{3x^2}{x^3-1}=\frac{2x}{x^2+x+1}\)
b) \(\frac{3}{(x-1)(x-2)}+\frac{2}{(x-3)(x-1)}=\frac{1}{(x-2)(x-3)}\)
c) \(1+\frac{1}{x+2}=\frac{12}{8+x^3}\)
d) \(\frac{13}{(x-3)(2x+7)}+\frac{1}{2x+7}=\frac{6}{(x-3)(x+3)}\)
Hướng dẫn giải chi tiết
Câu a:
\(\frac{1}{x-1}-\frac{3x^2}{x^3-1}=\frac{2x}{x^2+x+1}\)
Ta có: \(x^3-1=(x-1)(x^2+x+1)\)
\(=(x-1)[(x+\frac{1}{2})^2+\frac{3}{4}]\) cho nên x3 – 1 ≠ 0 khi x – 1 ≠ 0 ⇔ x ≠ 1
Vậy ĐKXĐ: x ≠ 1
Khử mẫu ta được:
\(x^2+x+1-3x^2=2x(x-1)\Leftrightarrow -2x^2+x+1=2x^2-2x\)
⇔4x2 − 3x − 1=0
⇔4x (x−1) + (x−1)=0
⇔(x−1)(4x+1)=0
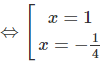
x = 1 không thỏa ĐKXĐ.
Vậy phương trình có nghiệm duy nhất x=−14x=−14
Câu b:
\(\frac{ 3}{(x-1)(x-2)}+\frac{2}{(x-3)(x-1)}=\frac{1}{(x-2)(x-3)}\)
ĐKXĐ: x ≠ 1, x ≠ 2, x ≠ 3
Khử mẫu ta được:
\(3(x-3)+2(x-2)=x-1\Leftrightarrow 3x-9+2x-4=x-1\)
⇔5x − 13= x − 1
⇔ 4x = 12
⇔ x = 3
x = 3 không thỏa mãn ĐKXĐ.
Vậy phương trình vô nghiệm.
Câu c:
\(1+\frac{1}{x+2}=\frac{12}{8+x^3}\)
Ta có: \(8+x^3=(x+2)(x^2-2x+4)\)
=(x + 2)[(x − 1)2+ 3]
Do đó: 8 + x2 ≠ 0 khi x + 2 ≠ 0 ⇔ x ≠ -2
Suy ra ĐKXĐ: x ≠ -2
Khử mẫu ta được:
\(x^3+8+x^2-2x+4=12\Leftrightarrow x^3+x^2-2x=0\)
⇔x(x2+x−2)=0
⇔x[x2 + 2x − x − 2]=0
⇔ x(x + 2)(x – 1) = 0
⇔ x(x -1) = 0
⇔x = 0 hay x = 1
x = 0, x = 1 thỏa ĐKXĐ của phương trình.
Vậy phương trình có tập nghiệm là S = {0;1}.
Câu d:
\(\frac{13}{(x-3)(2x+7)}+\frac{1}{2x+7}=\frac{6}{(x-3)(x+3)}\)
ĐKXĐ: \(x\neq 3,x\neq -3,x\neq -\frac{7}{2}\)
Khử mẫu ta được:
\(13(x+3)+(x-3)(x+3)=6(2x+7)\Leftrightarrow 13x+39+x^2-9=12x+42\)
⇔ x2 + x − 12=0
⇔ x2 + 4x − 3x − 12=0
⇔x(x+4) −3(x+4)=0
⇔(x−3)(x+4)=0
⇔ x =3 hoặc x = -4
x = 3 không thỏa ĐKXĐ.
Vậy phương trình có nghiệm duy nhất x = -4
-- Mod Toán 8 HỌC247
-


Tìm \(y\) sao cho giá trị của hai biểu thức \(\displaystyle{{y + 5} \over {y - 1}} - {{y + 1} \over {y - 3}}\) và \(\displaystyle{{ - 8} \over {\left( {y - 1} \right)\left( {y - 3} \right)}}\) bằng nhau.
bởi Bo bo
 08/02/2021
Theo dõi (0) 1 Trả lời
08/02/2021
Theo dõi (0) 1 Trả lời -


Tìm \(x\) sao cho giá trị của hai biểu thức \(\displaystyle{{6x - 1} \over {3x + 2}}\) và \(\displaystyle{{2x + 5} \over {x - 3}}\) bằng nhau.
bởi Trieu Tien
 07/02/2021
Theo dõi (0) 1 Trả lời
07/02/2021
Theo dõi (0) 1 Trả lời -


Tìm \(x\) sao cho giá trị của biểu thức \(\displaystyle{{2{x^2} - 3x - 2} \over {{x^2} - 4}}\) bằng \(2.\)
bởi Nguyễn Thị Lưu
 08/02/2021
Theo dõi (0) 1 Trả lời
08/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình sau: \(\displaystyle{{5 - 2x} \over 3} + {{\left( {x - 1} \right)\left( {x + 1} \right)} \over {3x - 1}} \) \(\displaystyle= {{\left( {x + 2} \right)\left( {1 - 3x} \right)} \over {9x - 3}}\)
bởi Ngoc Han
 07/02/2021
Theo dõi (0) 1 Trả lời
07/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình sau: \(\displaystyle{{5x - 2} \over {2 - 2x}} + {{2x - 1} \over 2} = 1 - {{{x^2} + x - 3} \over {1 - x}}\)
bởi thi trang
 08/02/2021
Theo dõi (0) 1 Trả lời
08/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình sau: \(\displaystyle{{{{\left( {x + 2} \right)}^2}} \over {2x - 3}} - 1 = {{{x^2} + 10} \over {2x - 3}}\)
bởi Mai Linh
 08/02/2021
Theo dõi (0) 1 Trả lời
08/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình sau: \(\displaystyle{{1 - x} \over {x + 1}} + 3 = {{2x + 3} \over {x + 1}}\)
bởi het roi
 08/02/2021
Theo dõi (0) 1 Trả lời
08/02/2021
Theo dõi (0) 1 Trả lời -


Hãy xét xem khẳng định sau đây đúng hay sai: Phương trình \(\displaystyle{{{x^2}\left( {x - 3} \right)} \over x} = 0\) có tập nghiệm là \(S = \{ 0; 3 \}\).
bởi Duy Quang
 08/02/2021
Theo dõi (0) 1 Trả lời
08/02/2021
Theo dõi (0) 1 Trả lời -


Hãy xét xem khẳng định sau đây đúng hay sai: Phương trình \(\displaystyle{{{x^2} + 2x + 1} \over {x + 1}} = 0\) có nghiệm là \(x = -1\).
bởi thu hằng
 08/02/2021
Theo dõi (0) 1 Trả lời
08/02/2021
Theo dõi (0) 1 Trả lời -


Hãy xét xem khẳng định sau đây đúng hay sai: Phương trình \(\displaystyle{{\left( {x + 2} \right)\left( {2x - 1} \right) - x - 2} \over {{x^2} - x + 1}} = 0\) có tập nghiệm là \(S = \{ -2; 1 \}\).
bởi Nhật Mai
 08/02/2021
Theo dõi (0) 1 Trả lời
08/02/2021
Theo dõi (0) 1 Trả lời -


Hãy xét xem khẳng định sau đây đúng hay sai: Phương trình \(\displaystyle{{4x - 8 + \left( {4 - 2x} \right)} \over {{x^2} + 1}} = 0\) có nghiệm là \(x = 2\).
bởi Minh Tuyen
 07/02/2021
Theo dõi (0) 1 Trả lời
07/02/2021
Theo dõi (0) 1 Trả lời -


Tìm các giá trị của \(a\) sao cho mỗi biểu thức sau có giá trị bằng \(2\): \(\dfrac{{10}}{3} - \dfrac{{3a - 1}}{{4a + 12}} - \dfrac{{7a + 2}}{{6a + 18}}\)
bởi Nhi Nhi
 02/02/2021
Theo dõi (0) 1 Trả lời
02/02/2021
Theo dõi (0) 1 Trả lời -


Tìm các giá trị của \(a\) sao cho mỗi biểu thức sau có giá trị bằng \(2\): \(\dfrac{{3a - 1}}{{3a + 1}} + \dfrac{{a - 3}}{{a + 3}}\)
bởi Lê Viết Khánh
 03/02/2021
Theo dõi (0) 1 Trả lời
03/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình: \({\left( {x + 1 + \dfrac{1}{x}} \right)^2} = {\left( {x - 1 - \dfrac{1}{x}} \right)^2}\)
bởi Chai Chai
 03/02/2021
Theo dõi (0) 1 Trả lời
03/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình: \(\dfrac{1}{x} + 2 = \left( {\dfrac{1}{x} + 2} \right)\left( {{x^2} + 1} \right)\)
bởi Van Dung
 03/02/2021
Theo dõi (0) 1 Trả lời
03/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình: \(1 + \dfrac{1}{{x + 2}} = \dfrac{{12}}{{8 + {x^3}}}\)
bởi Đào Lê Hương Quỳnh
 03/02/2021
Theo dõi (0) 1 Trả lời
03/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình: \(\dfrac{1}{{x - 1}} - \dfrac{{3{x^2}}}{{{x^3} - 1}} = \dfrac{{2x}}{{{x^2} + x + 1}}\)
bởi Bin Nguyễn
 03/02/2021
Theo dõi (0) 1 Trả lời
03/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình: \(\dfrac{{3x - 2}}{{x + 7}} = \dfrac{{6x + 1}}{{2x - 3}}\)
bởi Mai Vàng
 02/02/2021
Theo dõi (0) 1 Trả lời
02/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình: \(\dfrac{{x + 1}}{{x - 1}} - \dfrac{{x - 1}}{{x + 1}} = \dfrac{4}{{{x^2} - 1}}\)
bởi Tram Anh
 02/02/2021
Theo dõi (0) 1 Trả lời
02/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình: \(2x - \dfrac{{2{x^2}}}{{x + 3}} = \dfrac{{4x}}{{x + 3}} + \dfrac{2}{7}\)
bởi Kieu Oanh
 02/02/2021
Theo dõi (0) 1 Trả lời
02/02/2021
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải phương trình: \( \dfrac{5}{3x+2} = 2x -1\)
bởi minh thuận
 02/02/2021
Theo dõi (0) 1 Trả lời
02/02/2021
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải phương trình: \( \dfrac{2x-5}{x+5}= 3\)
bởi Trần Hoàng Mai
 03/02/2021
Theo dõi (0) 1 Trả lời
03/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình: \({3 \over {x - 2}} = {{2x - 1} \over {x - 2}} - x\)
bởi Nguyễn Thanh Thảo
 03/02/2021
Theo dõi (0) 1 Trả lời
03/02/2021
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 27 trang 22 SGK Toán 8 Tập 2
Bài tập 28 trang 22 SGK Toán 8 Tập 2
Bài tập 35 trang 11 SBT Toán 8 Tập 2
Bài tập 36 trang 11 SBT Toán 8 Tập 2
Bài tập 37 trang 11 SBT Toán 8 Tập 2
Bài tập 38 trang 12 SBT Toán 8 Tập 2
Bài tập 39 trang 12 SBT Toán 8 Tập 2
Bài tập 40 trang 12 SBT Toán 8 Tập 2
Bài tập 41 trang 13 SBT Toán 8 Tập 2





