Nội dung bài học sẽ giới thiệu đến các em khái niệm và tính chất của Tính chất đường trung trực của một đoạn thẳng - Luyện tập cùng với những dạng bài tập liên quan. Bên cạnh đó là những bài tập có hướng dẫn giải chi tiết sẽ giúp các em nắm được phương pháp giải các bài toán liên quan đề hai góc đối đỉnh.
Tóm tắt lý thuyết
1.1. Đường trung trực của tam giác
Trong một tam giác đường trung trực của một cạnh gọi là một đường trung trực của tam giác đó.
Mỗi tam giác có ba đường trung trực.
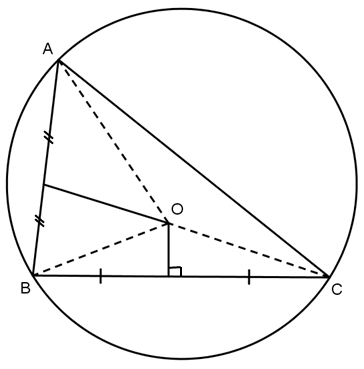
Nhận xét: Trong một tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung tuyến ứng với cạnh này.
1.2. Tính chất ba đường trung trực của tam giác
Định lý:
Ba đường trung trực của một tam giác cũng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.
Chú ý:
Vì giao điểm O của ba đường trung trực của tam giác ABC cách đều ba đỉnh của tam giác đó nên có một đường tròn tâm O đi qua ba đỉnh A, B, C.
Ta gọi đường tròn đó là đường tròn ngoại tiếp tam giác ABC.
Ví dụ 1: Cho tam giác ABC. Tìm một điểm O cách đều ba điểm A, B, C.
Giải
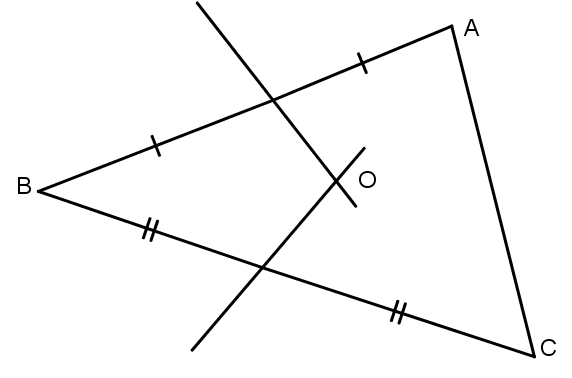
Điểm O cách đều hai điểm A, B nên suy ra điểm O nằm trên đường phân trung trực của đoạn thẳng AB.
Điểm O cách đều hai điểm B, C nên O nằm trên đường trung trực của đoạn thẳng BC.
Điểm O cách đều ba điểm A, B, C nên suy ra O là giao điểm của các đường trung trực của tam giác ABC.
Ví dụ 2: Tam giác ABC có \(\widehat A\) là góc tù. Các đường trung trực của AB và của AC cắt nhau ở O và cắt BC theo thứ tự ở P và E. Đường tròn tâm O bán kính OA đi qua những điểm nào trong hình vẽ.
Giải
.png)
Ta có O thuộc đường trung trực của đoạn AB nên suy ra \(OA{\rm{ }} = {\rm{ }}OB\,{\,^{(1)}}\)
Lại có O thuộc đường trung trực của đoạn AB nên suy ra \(OA{\rm{ }} = {\rm{ }}OC{\,^{\,(2)}}\)
Từ (1) và (2) suy ra OA = OB = OC.
Vậy đường tròn (O, OA) đi qua các điểm A, B, C.
Ví dụ 3: Xác định dạng của tam giác có giao điểm các phân giác trùng với giao điểm các đường trung trực.
Giải
Gọi O là giao điểm các phân giác của \(\Delta ABC\) thì ta có \(\widehat {OAB} = \widehat {OAC};\widehat {OBA} = \widehat {OBC};\widehat {OCA} = \widehat {OCB}.\) Nhưng O cũng là giao điểm của các đường trung trực nên OA = OB = OC.
Do đó \(\widehat {OAB} = \widehat {OBA};\widehat {OAC} = \widehat {OCA}.\) Từ đó suy ra \(\widehat A = \widehat B = \widehat C\)
Nên \(\Delta ABC\) đều.
Bài tập minh họa
Bài 1: Cho tam giác ABC và đường phân giác AK của góc A. Biết rằng giao điểm của đường phân giác của tam giác ABK trùng với giao điểm ba đường trung trực của tam giác ABC. Tìm số đo các góc của tam giác ABC.
Giải
.png)
Gọi O là giao điểm của ba đường phân giác của \(\Delta ABK\). Theo đề bài, O là giao điểm của ba đường trung trực của \(\Delta ABC\)
Vậy OA = OB = OC và các tam giác AOB, BOC, COA đều là các tam giác cân đỉnh O.
Gọi \(\widehat {OAB} = a\) thì \(\widehat {ABC} = 2a\) và \(\widehat {KAB} = 2a.\) Vì AK là đường phân giác của góc BAC nên nếu \(\widehat {KAB} = 2a\) thì \(\widehat {BAC} = 4a\).
Ta có: \(\Delta AOB = \Delta COB\) nên suy ra AB = CB
Vậy \(\Delta ABC\) là tam giác cân đỉnh B.
Suy ra \(\widehat {BAC} = \widehat {BAC}.\) Ta đã biết tổng ba góc của một tam giác bằng \({180^0}\), từ đó:
\(2a + 4a + 4a = {180^0} \Rightarrow 10a = {180^0} \Rightarrow a = {18^0}\)
Vậy số đo các góc của \(\Delta ABC\)là:
\(\widehat A = {72^0};\,\widehat B = {36^0};\widehat C = {72^0}\)
Bài 2: Trên ba cạnh AB, BC và CA của tam giác đều ABC. Lấy các điểm theo thứ tự M, N, P sao cho AM=BN=CP. Gọi O là giao điểm ba đường trung trực của tam giác ABC. Chứng minh O cũng là giao điểm ba đường trung trực của tam giác MNP.
Giải
.png)
Theo giả thiết O là giao điểm ba đường trung trực của tam giác ABC nên ta có:
OA = OB = OC
\( \Rightarrow \) Các tam giác AOM, BON và COP có:
AM = BN = CP (giả thiết)
\(\widehat {{A_1}} = \widehat {{B_1}} = \widehat {{C_1}} = {30^0}\) (Vì ABC là tam giác đều nên đường trung trực cũng là đường phân giác) và OA = OB = OC
\(\begin{array}{l} \Rightarrow \Delta AOM = \Delta BON = \Delta COP\,\,\,(c.g.c)\\ \Rightarrow \,\,OM = ON = OP\end{array}\)
Điều này chứng tỏ O là giao điểm của ba đường trung trực của tam giác MNP
3. Luyện tập Bài 8 Chương 3 Hình học 7
Qua bài giảng Tính chất ba đường trung trực của tam giác này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :
- Nắm vững định nghĩa đường trung trực của tam giác
- Tính chất ba đường trung trực của tam giác
3.1. Trắc nghiệm về Tính chất ba đường trung trực của tam giác
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Hình học 7 Chương 3 Bài 8 cực hay có đáp án và lời giải chi tiết.
-
- A. BM = MC
- B. ME = MD
- C. DM = MB
- D. M không thuộc đường trung trực của DE
-
- A. ΔABO = ΔCOE
- B. ΔBOA = ΔCOE
- C. ΔAOB = ΔCOE
- D. ΔABO = ΔOCE
-
- A. ΔAHD = ΔAKD
- B. AD là đường trung trực của đoạn thẳng HK
- C. AD là tia phân giác của góc HAK
- D. Cả A, B, C đều đúng
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.2. Bài tập SGK về Tính chất ba đường trung trực của tam giác
Các em có thể xem thêm phần hướng dẫn Giải bài tập Hình học 7 Chương 3 Bài 8 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Bài tập 52 trang 79 SGK Toán 7 Tập 2
Bài tập 53 trang 80 SGK Toán 7 Tập 2
Bài tập 54 trang 80 SGK Toán 7 Tập 2
Bài tập 55 trang 80 SGK Toán 7 Tập 2
Bài tập 56 trang 80 SGK Toán 7 Tập 2
Bài tập 57 trang 80 SGK Toán 7 Tập 2
Bài tập 64 trang 49 SBT Toán 7 Tập 2
Bài tập 65 trang 49 SBT Toán 7 Tập 2
Bài tập 66 trang 49 SBT Toán 7 Tập 2
Bài tập 67 trang 50 SBT Toán 7 Tập 2
Bài tập 68 trang 50 SBT Toán 7 Tập 2
Bài tập 69 trang 50 SBT Toán 7 Tập 2
4. Hỏi đáp Bài 8 Chương 3 Hình học 7
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 7 HỌC247













