Bài tập 57 trang 117 SGK Toán 12 NC
Trên hình bên cho hai đường cong (C1) (đường nét liền) và (C2) (đường nét đứt) được vẽ trên cùng một mặt phẳng tọa độ. Biết rằng mỗi đường cong ấy là đồ thị của ột trong hai hàm số lũy thừa y = x - 2 và \(y = {x^{ - \frac{1}{2}}}\) (x > 0). Chỉ dựa vào tính chất của lũy thừa, có thể nhận biết đường cong nào là đồ thị của hàm số nào được không?
Hãy nêu rõ lập luận.
.png)
Hướng dẫn giải chi tiết
Giả sử (C1) và (C2) theo thứ tự là đồ thị của hàm số \(y = {x^\alpha }\) và \(y = {x^\beta }\) (α và β là -2 hoặc −1/2). Trên đồ thị, ta thấy trên khoảng (1;+∞), đường cong (C2) nằm trên đường cong (C1), nghĩa là khi x > 1 ta có bất đẳng thức \({x^\beta } > {x^\alpha }\) .
Vậy β = −1/2 và α = −2.
Vậy đường (C1) là đồ thị của hàm số y = x-2, (C2) là đồ thị hàm số \(y = {x^{ - \frac{1}{2}}}\).
-- Mod Toán 12 HỌC247
-


Giải phương trình 6^(x+1)-5.4^x=9^x
bởi Quang Khải
 01/01/2020
Câu 2010
01/01/2020
Câu 2010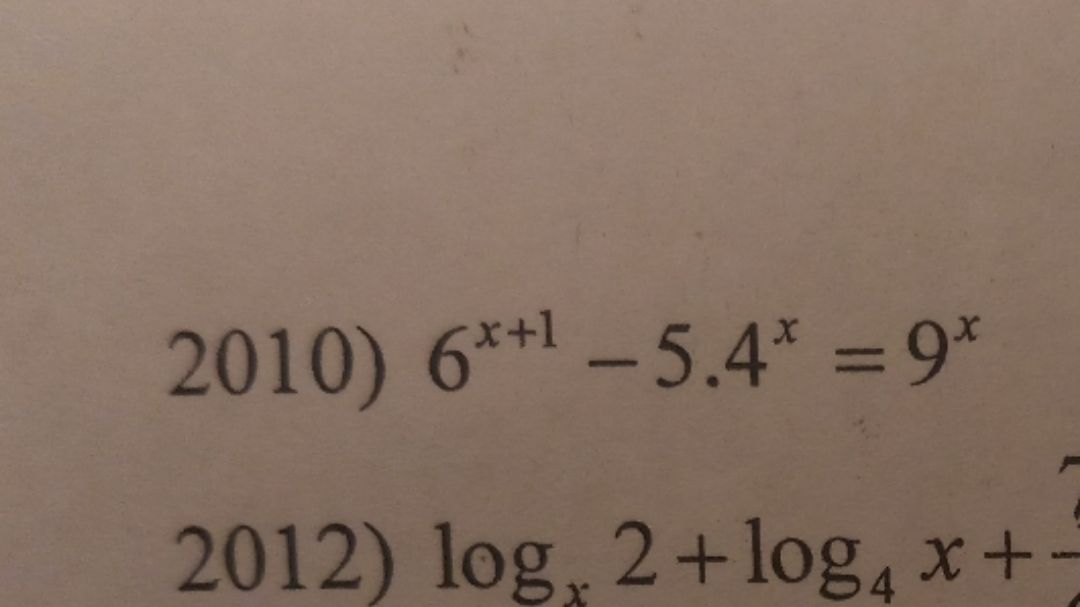 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cách tìm tham số m để hàm số đồng biến?
bởi Thanh Thanh
 26/12/2019
Tìm hàm mTheo dõi (0) 0 Trả lời
26/12/2019
Tìm hàm mTheo dõi (0) 0 Trả lời -


Tìm tập xác định D của hàm số y= (x-1) mũ pi/3
bởi Ngọc Ánh
 22/12/2019
Tìm tập xác định dTheo dõi (1) 8 Trả lời
22/12/2019
Tìm tập xác định dTheo dõi (1) 8 Trả lời -

 Tính y'.cos y".sĩnTheo dõi (0) 1 Trả lời
Tính y'.cos y".sĩnTheo dõi (0) 1 Trả lời -

 6^x (3-m)2^x-m= 0.Tim tập hợp các giá trị của m để hàm số có nghiệm trên khoảng (0;1)Theo dõi (0) 3 Trả lời
6^x (3-m)2^x-m= 0.Tim tập hợp các giá trị của m để hàm số có nghiệm trên khoảng (0;1)Theo dõi (0) 3 Trả lời -


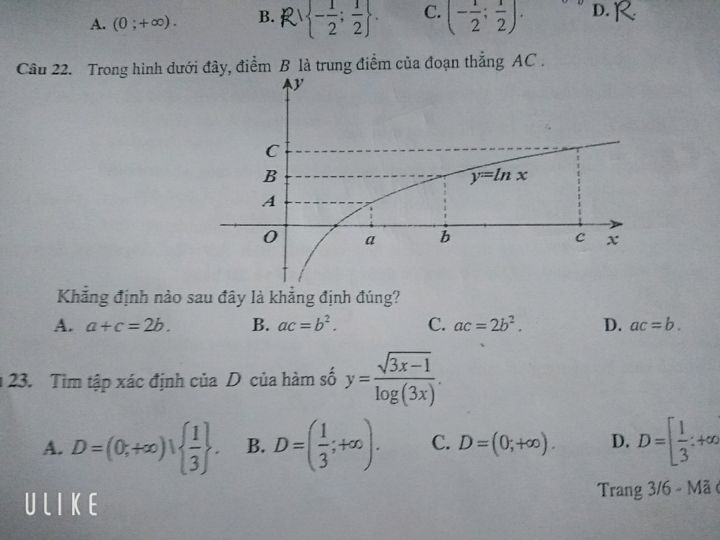
Tìm TXĐ của hàm số y=căn(3x-1)/log(3x)
bởi Tạ Thị Bích Lụa
 13/12/2019
13/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời





