Giải bài 4 tr 18 sách GK Toán Hình lớp 12
Cho hình bát diện đều ABCDEF (h.1.24).
Chứng minh rằng :
a) Các đoạn thẳng AF, BD và CE đôi một vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.
b) ABFD, AEFC và BCDE là những hình vuông.
Hướng dẫn giải chi tiết bài 4
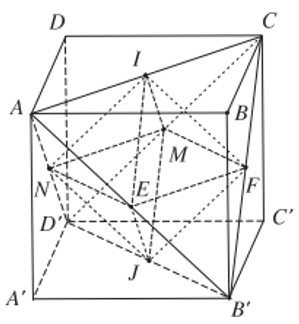
Câu a:
Do B, C, D, E cách đều A và F nên chúng đồng phẳng (cùng thuộc mặt phẳng trung trực của AF).
Tương tự, A, B, F, D đồng phẳng và A, C, F, E đồng phẳng
Gọi I là giao của (AF) với (BCDE). Khi đó B, I, D là những điểm chung của hai mặt phẳng (BCDE) và (ABFD) nên chúng thẳng hàng. Tương tự, E, I , C thẳng hàng.
Vậy AF, BD, CE đồng quy tại I.
Vì BCDE là hình thoi nên BD vuông góc với BC và cắt BC tại I là trung điểm của mỗi đường. I là trung điểm của AF và AF vuông góc với BD và EC, do đó các đoạn thẳng AF, BD, và CE đôi một vuông góc với nhau cắt nhau tại trung điểm của chúng.
Câu b:
Do AI vuông góc (BCDE) và AB = AC =AD = AE nên IB = IC= ID = IE. Từ đó suy ra hình thoi BCDE là hình vuông. Tương tự, ABFD, AEFC là những hình vuông.
-- Mod Toán 12 HỌC247
-


Tìm ví dụ về khối đa diện lồi và khối đa diện không lồi trong thực tế.
Theo dõi (0) 1 Trả lời -


A. Khối lập phương là khối đa diện lồi
B. Khối chóp là khối đa diện lồi
C. Khối lăng trụ là khối đa diện lồi
D. Ghép hai khối đa diện lồi sẽ được một khối đa diện lồi
Theo dõi (0) 5 Trả lời -


Cho đa diện đều có các mệnh đề sau, mệnh đề nào sai ?
bởi Tra xanh
 26/01/2021
26/01/2021
A. Số mặt của một hình đa diện đều luôn là số chẵn
B. Số đỉnh của một hình đa diện đều luôn là số chẵn
C. Số cạnh của một hình đa diện đều luôn là số chẵn
D. Tồn tại một hình đa diện đều có số cạnh là số lẻ
Theo dõi (0) 4 Trả lời -


Khối 12 mặt đều có bao nhiêu đỉnh ?
bởi Nguyen Dat
 25/01/2021
25/01/2021
A. 10 đỉnh
B. 12 đỉnh
C. 18 đỉnh
D. 20 đỉnh
Theo dõi (2) 6 Trả lời -


Cho tứ diện OABC có OA,OB,OC đôi một vuông góc với nhau và OA=OB=OC. Gọi M là trung điểm của BC. Góc giữa hai đường thẳng OM và AB
bởi Thu Vân
 26/05/2020
Góc giữa hai đường thẳng
26/05/2020
Góc giữa hai đường thẳng Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 2 trang 18 SGK Hình học 12
Bài tập 3 trang 18 SGK Hình học 12
Bài tập 1.6 trang 12 SBT Hình học 12
Bài tập 1.7 trang 12 SBT Hình học 12
Bài tập 1.8 trang 12 SBT Hình học 12
Bài tập 1.9 trang 12 SBT Hình học 12
Bài tập 6 trang 15 SGK Hình học 12 NC
Bài tập 7 trang 15 SGK Hình học 12 NC
Bài tập 8 trang 15 SGK Hình học 12 NC
Bài tập 9 trang 15 SGK Hình học 12 NC
Bài tập 10 trang 15 SGK Hình học 12 NC
Bài tập 11 trang 20 SGK Hình học 12 NC
Bài tập 12 trang 20 SGK Hình học 12 NC
Bài tập 13 trang 20 SGK Hình học 12 NC






