Bài tập 12 trang 20 SGK Hình học 12 NC
Cho một khối tứ diện đều. Hãy chứng minh rằng:
a) Các trọng tâm của các mặt của nó là các đỉnh của một khối tứ diện đều.
b) Các trung điểm của các cạnh của nó là các đỉnh của một khối tám mặt đều.
Hướng dẫn giải chi tiết
a)
.jpg)
Gọi A′, B′, C′, D′ lần lượt là trọng tâm của tam giác BCD, CDA, BDA, ABC của tứ diện đều ABCD có trọng tâm G.
Ta có \(\overrightarrow {GA'} = - \frac{1}{3}\overrightarrow {GA} \)
Gọi \( V_{\left( {G;\frac{{ - 1}}{3}} \right)}}\) là phép vị tự tâm G tỉ số −1/3 ta có A′, B′, C′, D′ lần lượt là ảnh của A, B, C, D qua phép vị tự V. Từ đó suy ra:
\(\begin{array}{l}
\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{C'D'}}{{CD}} = \frac{{D'A'}}{{DA}}\\
= \frac{{A'C'}}{{AC}} = \frac{{B'D'}}{{BD}} = \frac{1}{3}
\end{array}\)
Do đó nếu ABCD là tứ diện đều thì A′B′C′D′ cũng là tứ diện đều.
b)
.jpg)
Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, CD, AC, BD, AD, BC của khối tứ diện đều ABCD. Khi đó, tám tam giác MPR, MRQ, MQS, MSP, NPR, NRQ, NQS, NSP là những tam giác đều, chúng làm thành khối đa diện với các đỉnh là M, N, P, Q, R, S mà mỗi đỉnh là đỉnh chung của bốn cạnh. Vậy đó là khối tám mặt đều.
-- Mod Toán 12 HỌC247
-


Tính khoảng cách 2 đường thẳng chéo nhau BC và AA' biết góc giữa cạnh bên với đáy= 60^0
bởi Hồ Phương Trinh
 11/10/2018
11/10/2018
cho lăng trụ ABC.A'B'C' có mặt đáy là tam giác đều cạnh AB=2a. Hình chiếu vuông góc của A' lên mp (ABC) trùng vs trung điểm H của AB. bK GÓC giữa cạnh bên vs mp đáy= 600.Tính khoàn cách 2 đường thẳng chéo nhau BC và AA' theo a là
A. (2 a.căn 15)/5
B. 9a căn 15 )/5
C. (2a căn 21)/7
D. (a căn 39)/13
Theo dõi (0) 2 Trả lời -


Bài 2 trang 18 SGK Hình học 12
bởi Nguyễn Hồng Tiến
 10/10/2018
Bài 2 (SGK trang 18)
10/10/2018
Bài 2 (SGK trang 18)Cho hình lập phương (H). Gọi (H') là hình bát diện đều có các đỉnh là tâm các mặt của (H). Tính tỉ số diện tích toàn phần của (H) và (H') ?
Theo dõi (0) 1 Trả lời -


Bài 1.9 trang 14 sách bài tập Hình học 12
bởi Lê Vinh
 10/10/2018
Bài 1.9 (Sách bài tập trang 14)
10/10/2018
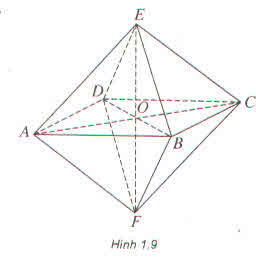
Bài 1.9 (Sách bài tập trang 14)Cho khối bát diện đều ABCDEF (h.1.9). Gọi O là giao điểm của AC, BD, M và N theo thứ tự là trung điểm của AB và AE. Tính diện tích thiết diện tạo bởi khối bát đó với mặt phẳng (OMN) ?
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Bài 1.8 trang 14 sách bài tập Hình học 12
bởi het roi
 10/10/2018
Bài 1.8 (Sách bài tập trang 14)
10/10/2018
Bài 1.8 (Sách bài tập trang 14)Cho một bát diện đều. Hãy chỉ ra một mặt phẳng đối xứng, một tâm đối xứng và một trục đối xứng của nó ?
Theo dõi (0) 1 Trả lời -


Cho ba đoạn thẳng bằng nhau, đôi một vuông góc với nhau và cắt nhau tại trung điểm của chúng
bởi Thuy Kim
 25/08/2018
Bài 1.7 (Sách bài tập trang 14)
25/08/2018
Bài 1.7 (Sách bài tập trang 14)Cho ba đoạn thẳng bằng nhau, đôi một vuông góc với nhau và cắt nhau tại trung điểm của chúng. Chứng minh rằng các đầu mút của ba đoạn thẳng ấy là các đỉnh của một hình bát diện đều ?
Theo dõi (0) 1 Trả lời





