Giải bài 4.38 tr 171 SBT Toán 11
Tìm giá trị của tham số để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}
\frac{{\sqrt x - 1}}{{{x^2} - 1}},x \ne 1\\
{m^2},\,\,\,\,\,\,\,\,x = 1
\end{array} \right.\) liên tục trên
Hướng dẫn giải chi tiết
Với thì \(f\left( x \right) = \frac{{\sqrt x - 1}}{{{x^2} - 1}}\) là hàm đa thức xác định trên \((0; + \infty )\backslash \left\{ 1 \right\}\) nên liên tục trên các khoảng và
Với thì .
Để hàm số liên tục trên thì \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = f\left( 1 \right)\)
Ta có: \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = {m^2}\)
Vậy để hàm số liên tục trên thì \(f(1) = \frac{1}{4} \Leftrightarrow {m^2} = \frac{1}{4} \Leftrightarrow m = \pm \frac{1}{2}\)
-- Mod Toán 11 HỌC247
-


Chọn khẳng định sai?
bởi Ngọc Ngọc
 13/06/2020
13/06/2020
Giải giúp ạ...mơn nhìu.
Câu 5
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Xét tính liên tục của hàm số tại điểm \(y = f(x) = \left\{ \begin{array}{l} \frac{{6{x^2} - 7x - 13}}{{x + 1}},\,x \ne - 1\\ 10x - 9,\,\,x = - 1 \end{array} \right.\)?
bởi Diễm My
 12/06/2020
12/06/2020
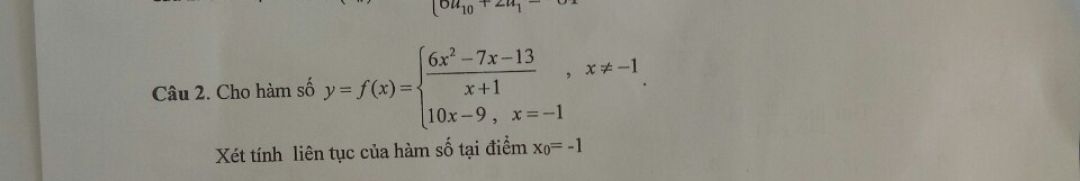 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính a,b để hàm số liên tục tại 2?
bởi Lâm Oanh
 07/06/2020
07/06/2020
Bài 3
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho hàm số \(f\left( x \right) = \sqrt {{x^2} - 4} \). Chọn câu đúng trong các câu sau:
bởi Nguyễn Lệ Diễm
 29/05/2020
29/05/2020
(I) f(x) liên tục tại x = 2
(II) f(x) gián đoạn tại x = 2
(III) f(x) liên tục trên đoạn [-2, 2]
A. Chỉ (I) và (III) B. Chỉ (I)
C. Chỉ (II) D. Chỉ (II) và (III)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 4.36 trang 171 SBT Toán 11
Bài tập 4.37 trang 171 SBT Toán 11
Bài tập 4.39 trang 171 SBT Toán 11
Bài tập 4.40 trang 171 SBT Toán 11
Bài tập 4.41 trang 172 SBT Toán 11
Bài tập 4.42 trang 172 SBT Toán 11
Bài tập 4.43 trang 172 SBT Toán 11
Bài tập 4.44 trang 172 SBT Toán 11
Bài tập 4.45 trang 172 SBT Toán 11
Bài tập 4.46 trang 172 SBT Toán 11
Bài tập 46 trang 172 SGK Toán 11 NC
Bài tập 47 trang 172 SGK Toán 11 NC
Bài tập 48 trang 173 SGK Toán 11 NC
Bài tập 49 trang 173 SGK Toán 11 NC
Bài tập 50 trang 175 SGK Toán 11 NC
Bài tập 51 trang 175 SGK Toán 11 NC





