Bài tập 48 trang 173 SGK Toán 11 NC
Chứng minh rằng mỗi hàm số sau đây liên tục trên tập xác định của nó:
a. \(f\left( x \right) = \frac{{{x^2} + 3x + 4}}{{2x + 1}}\)
b. \(f\left( x \right) = \sqrt {1 - x} + \sqrt {2 - x} \)
Hướng dẫn giải chi tiết
a) Tập xác định của hàm số f là \(R\backslash \left\{ {\frac{1}{2}} \right\}\).
Hàm số phân thức hữu tỉ nên f liên tục trên tập xác định của nó, tức là liên tục trên các khoảng \(\left( { - \infty ; - \frac{1}{2}} \right)\) và \(\left( { - \frac{1}{2}; + \infty } \right)\).
b) Hàm số f xác định khi và chỉ khi:
\(\left\{ \begin{array}{l}
1 - x \ge 0\\
2 - x \ge 0
\end{array} \right. \Leftrightarrow x \le 1\)
Do đó tập xác định của hàm số f là \(\left( { - \infty ;1} \right]\)
Với mọi \({x_0} \in \left( { - \infty ;1} \right)\), ta có:
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {\sqrt {1 - x} + \sqrt {2 - x} } \right)\\
= \sqrt {1 - {x_0}} + \sqrt {2 - {x_0}} = f\left( {{x_0}} \right)
\end{array}\)
Vậy hàm số f liên tục trên khoảng \(\left( { - \infty ;1} \right)\). Ngoài ra
\(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \left( {\sqrt {1 - x} + \sqrt {2 - x} } \right) = 1 = f\left( 1 \right)\)
Do đó hàm số f liên tục trên \(\left( { - \infty ;1} \right]\)
-- Mod Toán 11 HỌC247
-


 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Toán về hàm số liên tục
bởi Lê Văn Đạt
 16/03/2020
Làm dùm mình với
16/03/2020
Làm dùm mình với Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính giới hạn
bởi Võ Nguyễn Yến Nhi
 14/03/2020
14/03/2020
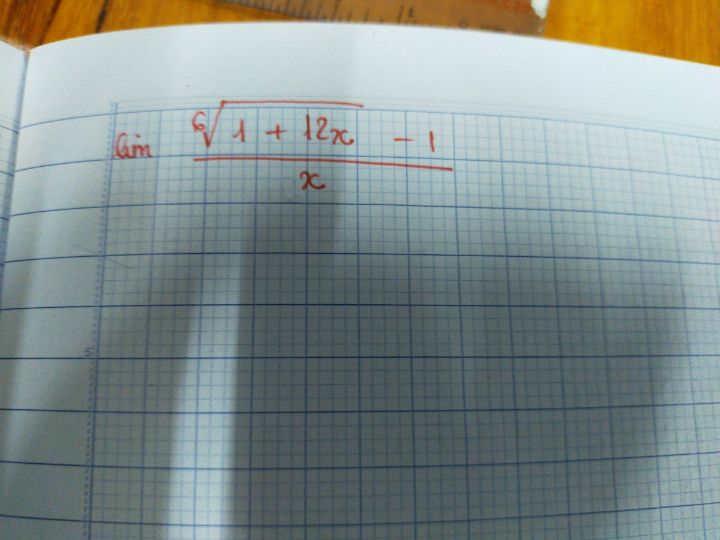 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Ứng dụng của hàm số liên tục trong thực tế là gì ạ??
bởi uyen thao
 04/03/2020
Ứng dụng của hàm số liên tục trong thực tế là gì ạ??Theo dõi (1) 0 Trả lời
04/03/2020
Ứng dụng của hàm số liên tục trong thực tế là gì ạ??Theo dõi (1) 0 Trả lời





