Giải bài 1 tr 59 sách GK Toán Hình lớp 11
Cho tứ diện ABCD. Gọi P, Q, R, S là bốn điểm lần lượt lấy trên bốn cạnh AB, BC, CD, DA. Chứng minh rằng nếu bốn điểm P, Q, R, S đồng phẳng thì
a) Ba đường thẳng PQ, SR, AC hoặc song song hoặc đồng quy
b) Ba đường thẳng PS, RQ, BD hoặc song song hặc đồng quy
Hướng dẫn giải chi tiết bài 1
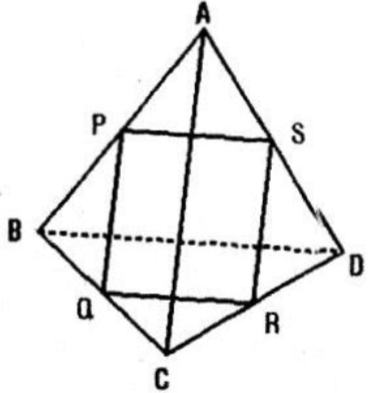
Câu a:
Ta có:
\(\begin{matrix} (PQRS)\cap (ABC)=PQ\\ (PQRS)\cap (ACD)=RS\\ (ABC) \cap (ACD)=AC \ \ \ \end{matrix}\)
Theo định lí về giao tuyến của 3 mp thì PQ, RS, AC hoặc đôi một cắt nhau hoặc đồng quy.
Câu b:
Chứng minh tương tự ta được ba đường thẳng PS, RQ, và BD hoặc song song hoặc đồng quy.
-- Mod Toán 11 HỌC247
-
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là một tứ giác lồi. Gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\). Xác định thiết diện của hình chóp cắt bởi mặt phẳng \((α)\) đi qua \(O\), song song với \(AB\) và \(SC\). Thiết diện đó là hình gì?
bởi Long lanh
26/02/2021
Theo dõi (0) 1 Trả lời -
Cho tứ diện \(ABCD\). Trên cạnh \(AB\) lấy một điểm \(M\). Cho \((α)\) là mặt phẳng qua \(M\), song song với hai đường thẳng \(AC\) và \(BD\). Tìm giao tuyến của \((α)\) với các mặt tứ diện.
bởi Anh Trần
26/02/2021
Theo dõi (0) 1 Trả lời -
Cho hai hình bình hành \(ABCD\) và \(ABEF\) không cùng nằm trong một mặt phẳng. Gọi \(O\) và \(O'\) lần lượt là tâm của các hình bình hành \(ABCD\) và \(ABEF\). Chứng minh rằng đường thằng \(OO'\) song song với các mặt phẳng \((ADF)\) và \((BCF)\).
bởi Nguyễn Quang Minh Tú
26/02/2021
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2 trang 59 SGK Hình học 11
Bài tập 3 trang 60 SGK Hình học 11
Bài tập 2.10 trang 67 SBT Hình học 11
Bài tập 2.11 trang 67 SBT Hình học 11
Bài tập 2.12 trang 67 SBT Hình học 11
Bài tập 2.13 trang 68 SBT Hình học 11
Bài tập 2.14 trang 68 SBT Hình học 11
Bài tập 2.15 trang 68 SBT Hình học 11
Bài tập 17 trang 55 SGK Hình học 11 NC
Bài tập 18 trang 55 SGK Hình học 11 NC
Bài tập 19 trang 55 SGK Hình học 11 NC
Bài tập 20 trang 55 SGK Hình học 11 NC
