Giải bài 2 tr 59 sách GK Toán Hình lớp 11
Cho tứ diện ABCD và ba điểm P, Q, R lần lượt trên ba cạnh AB, CD, BC. Tìm giao điểm S của AD và mặt phẳng (PQR) trong hai trường hợp sau đây.
a) PR song song với AC
b) PR cắt AC
Hướng dẫn giải chi tiết bài 2
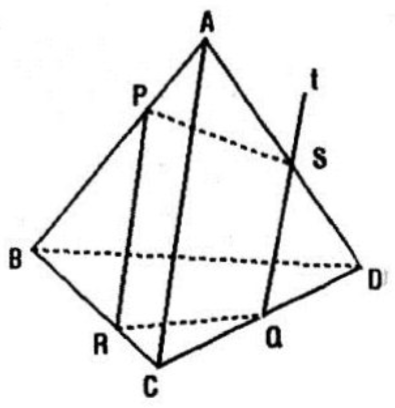
Câu a:
Trường hợp PR // AC
Hai mp(PQR) và (ACD) có điểm chung Q và lần lượt chứa 2 đường thẳng song song PR và AC ⇒ Giao tuyến của (PQR) và (ACD) qua Q và song song với AC.
\(\Rightarrow (PQR)\cap (ACD)=Qt\) với Qt // AC.
Gọi S là giao điểm của Qt và AD.
Khi đó S là giao điểm của AD và (PQR)
Câu b:
Trường hợp PQ cắt AC.
Giả sử I là giao điểm của PR và AC \(\Rightarrow (PQR)\cap (ACD)=QI\)
Trong mp(ACD), gọi S là giao điểm của QI và AD
⇒ S là giao điểm của AD và mp(PQR).
-- Mod Toán 11 HỌC247
-
Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Khẳng định nào sau đây là đúng?
bởi Kim Xuyen
22/01/2021
A. giao tuyến của (SAB) và (SCD) là điểm S.
B. giao tuyến của (SAB) và (SCD) là đường thẳng đi qua S và song song với AB.
C. giao tuyến của (SAB) và (SCD) là đường thẳng đi qua S và cắt AB.
D. giao tuyến của (SAB) và (SCD) là đường thẳng đi qua S và chéo nhau với AB.
Theo dõi (0) 1 Trả lời -
Cho hình chóp S. ABCD có đáy là một tứ giác lồi. gọi M và N lần lượt là trong tâm của tam giác SAB và SAD. Khẳng định nào sau đây là đúng?
bởi Nguyễn Hoài Thương
21/01/2021
A. MN // PQ với P là giao điểm của SM và AB; Q là giao điểm của SN và AD.
B. MN, BD chéo nhau.
C. MN và BD cắt nhau.
D. MN là đường trung bình của tam giác IBD với I là trung điểm của SA.
Theo dõi (0) 1 Trả lời
