Bài tập 19 trang 55 SGK Hình học 11 NC
Cho tứ diện ABCD. Bốn điểm P, Q, R, S lần lượt nằm trên bốn cạnh AB, BC, CD, DA và không trùng với các đỉnh của tứ diện. Chứng minh rằng
a. Bốn điểm P, Q, R, S đồng phẳng khi và chỉ khi ba đường thẳng PQ, RS, AC hoặc đôi một song song hoặc đồng quy
b. Bốn điểm P, Q, R, S đồng phẳng khi và chỉ khi ba đường thẳng PS, RQ, BD hoặc đôi một song song hoặc đồng quy
Hướng dẫn giải chi tiết
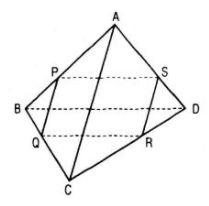
Nếu P, Q, R, S đồng phẳng thì chúng cùng thuộc mặt phẳng (PQRS).
Ta có:
(PQRS) ∩ (ABC) = PQ
(PQRS) ∩ (ACD) = RS
(ABC) ∩ (ACD) = AC
Theo định lí về giao tuyến của ba mặt phẳng thì PQ, SR, AC hoặc đôi một song song hoặc đồng quy.
Ngược lại, nếu ba đường thẳng PQ, AC, RS hoặc đôi một song song hoặc đồng quy thì hai đường thẳng PQ và RS cùng thuộc một mặt phẳng, từ đó bốn điểm P, Q, R, S đồng phẳng.
-- Mod Toán 11 HỌC247
-


Cho hình chóp S.ABCD có đáy ABCD là hình thang (đáy lớn AB). Lấy I; K lần lượt là trung điểm AD; BC và G là trọng tâm tam giác SAB
a)Tìm giao tuyến của 2 mặt phẳng (IKG) và (SAD)
b)Xác định thiết diện của mp (IKG) với hình chóp? Tìm điều kiện của AB và CD để thiết diện là hình bình hànhTheo dõi (0) 0 Trả lời






