Giải bài 2.15 tr 68 SBT Hình học 11
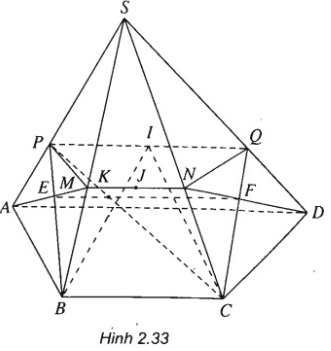
Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy là AD và BC. Biết AD = a, BC = b. Gọi I và J lần lượt là trọng tâm của các tam giác SAD và SBC. Mặt phẳng (ADJ) cắt SB, SC lần lượt tại M, N. Mặt phẳng (BCI) cắt SA, SD lần lượt tại P, Q.
a) Chứng minh MN song song với PQ.
b) Giả sử AM cắt BP tại E; CQ cắt DN tại F. Chứng minh rằng EF song song với MN và PQ. Tính EF theo a và b.
Hướng dẫn giải chi tiết
a) Ta có: I ∈ (SAD) ⇒ I ∈ (SAD) ∩ (IBC)
Vậy (\left\{ \begin{array}{l}
AD\parallel BC\\
AD \subset \left( {SAD} \right)\\
BC \subset \left( {IBC} \right)
\end{array} \right. \Rightarrow \left( {SAD} \right) \cap \left( {IBC} \right) = PQ\) và PQ //AD // BC (1)
Tương tự: J ∈ (SBC) ⇒ J ∈ (SBC) ∩ (JAD)
Vậy \(\left\{ \begin{array}{l}
AD\parallel BC\\
AD \subset \left( {JAD} \right)\\
BC \subset \left( {SBC} \right)
\end{array} \right. \Rightarrow \left( {JAD} \right) \cap \left( {SBC} \right) = MN\) và \(MN\parallel BC\parallel AD\) (2)
Từ (1) và (2) suy ra PQ // MN.
b) Ta có: \(\begin{array}{l}
E = AM \cap BP \Rightarrow \left\{ \begin{array}{l}
E \in \left( {AMND} \right)\\
E \in \left( {PBCQ} \right)
\end{array} \right.\\
F = DN \cap CQ \Rightarrow \left\{ \begin{array}{l}
F \in \left( {AMND} \right)\\
F \in \left( {PBCQ} \right)
\end{array} \right.
\end{array}\)
Do đó: EF = (AMND) ∩ (PBCQ)
Mà \(\left\{ \begin{array}{l}
AD\parallel BC\\
MN\parallel PQ
\end{array} \right.\) suy ra \(EF\parallel AD\parallel BC\parallel MN\parallel PQ\).
Tính EF:
CP ∩ EF = K ⇒ EF = EK + KF
\(\begin{array}{l}
EK\parallel BC \Rightarrow \frac{{EK}}{{BC}} = \frac{{PE}}{{PB}}\\
PM\parallel AB \Rightarrow \frac{{PE}}{{EB}} = \frac{{PM}}{{AB}}
\end{array}\)
Mà \(\frac{{PM}}{{AB}} = \frac{{SP}}{{SA}} = \frac{2}{3}\) suy ra \(\frac{{PE}}{{EB}} = \frac{2}{3}\).
Từ (∗) suy ra
\(\frac{{EK}}{{BC}} = \frac{{PE}}{{PB}} = \frac{{PE}}{{PE + EB}} = \frac{1}{{1 + \frac{{EB}}{{PE}}}} = \frac{1}{{1 + \frac{3}{2}}} = \frac{2}{5}\)
\( \Rightarrow EK = \frac{2}{5}BC = \frac{2}{5}b\)
Tương tự ta tính được \(KF = \frac{{2a}}{5}\)
Vậy: \(EF = \frac{2}{5}a + \frac{2}{5}b = \frac{2}{5}\left( {a + b} \right)\)
-- Mod Toán 11 HỌC247
-


Tư diện ABCD có các cạnh bằng a, M là trung điểm của BC. Tính cossin góc giữa 2 đường thẳng AB và DM.
bởi Liệu Tuyến
 19/03/2020
Là câu hỏi trênTheo dõi (0) 1 Trả lời
19/03/2020
Là câu hỏi trênTheo dõi (0) 1 Trả lời -


Tìm giao tuyến của (SAD) và (SBC) biết hình chóp S.ABCD có đáy ABCD là hình bình hành
bởi Nhungg Nhungg
 27/02/2020
27/02/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm giao tuyến của mặt phẳng SAB và SC biết M, N lần lượt là trung điểm của AD và SB
bởi HuyềnThu Nguyễn
 26/12/2019
Cho hinh cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M,N lần lượt là trung điểm của AD và SB. Tìm giao tuyến của mặt phẳng SAB và SCTheo dõi (0) 1 Trả lời
26/12/2019
Cho hinh cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M,N lần lượt là trung điểm của AD và SB. Tìm giao tuyến của mặt phẳng SAB và SCTheo dõi (0) 1 Trả lời