Giải bài 2.13 tr 68 SBT Hình học 11
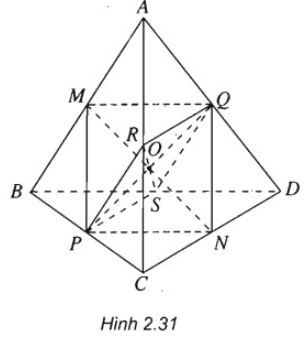
Cho tứ diện ABCD. Gọi M, N, P, Q, R và S lần lượt trung điểm của AB, CD, BC, AD, AC và BD. Chứng minh rằng tứ giác MNPQ là hình bình hành. Từ đó suy ra ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.
Hướng dẫn giải chi tiết
Trong tam giác ABC ta có:
MP // AC và MP = \(\frac{{AC}}{2}\).
Trong tam giác ACD ta có:
QN // AC và QN = \(\frac{{AC}}{2}\).
Từ đó suy ra MP // QN ⇒ Tứ giác MNPQ là hình bình hành.
Do vậy hai đường chéo MN và PQ cắt nhau tại trung điểm O của mỗi đường.
Tương tự: PR // QS và PR = QS = \(\frac{{AB}}{2}\). Do đó tứ giác PQRS là hình bình hành.
Suy ra hai đường chéo RS và PQ cắt nhau tại trung điểm O của PQ và OR = OS
Vậy ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.
-- Mod Toán 11 HỌC247
-


Cho hai đường thẳng a và b chéo nhau. Một đường thẳng c song song với a. khẳng định nào sau đây là đúng?
bởi khanh nguyen
 22/01/2021
22/01/2021
A. b và c chéo nhau
B. b và c cắt nhau
C. b và c chéo nhau hoặc cắt nhau
D. b và c song song với nhau
Theo dõi (0) 1 Trả lời -


Trong không gian cho ba đường thẳng a, b và c. Trong các phát biểu sau, phát biểu nào là đúng?
bởi Trần Thị Trang
 22/01/2021
22/01/2021
A. Nếu hai đường thẳng cùng song song với một đường thẳng thứ ba thì chúng song song với nhau
B. Nếu hai đường thẳng cùng chéo nhau với một đường thẳng thứ ba thì chúng chéo nhau.
C. Nếu đường thẳng a song song với b, đường thẳng b và c chéo nhau thì a và c chéo nhau hoặc cắt nhau.
D. Nếu hai đường thẳng a và b cắt nhau, b và c cắt nhau tì a và c cắt nhau hoặc song song.
Theo dõi (0) 1 Trả lời -


Trong các phát biểu sau, phát biểu nào đúng?
bởi Sam sung
 21/01/2021
21/01/2021
A. Hai đường thẳng không có điểm chung thì song song với nhau
B. Hai đường thẳng không có điểm chung thì chéo nhau
C. Hai đường thẳng phân biệt không cắt nhau thì song song
D. Hai đường thẳng không cùng nằm trên một mặt phẳng thì chéo nhau.
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2.11 trang 67 SBT Hình học 11
Bài tập 2.12 trang 67 SBT Hình học 11
Bài tập 2.14 trang 68 SBT Hình học 11
Bài tập 2.15 trang 68 SBT Hình học 11
Bài tập 17 trang 55 SGK Hình học 11 NC
Bài tập 18 trang 55 SGK Hình học 11 NC
Bài tập 19 trang 55 SGK Hình học 11 NC
Bài tập 20 trang 55 SGK Hình học 11 NC