Bài tập 18 trang 55 SGK Hình học 11 NC
Cho tứ diện ABCD. Gọi M, N là hai điểm phân biệt cùng thuộc đường thẳng AB; P, Q là hai điểm phân biệt cùng thuộc đường thẳng CD. Xét vị trí tương đối của hai đường thẳng MQ, NP và vị trí tương đối của hai đường thẳng MP, NQ
Hướng dẫn giải chi tiết
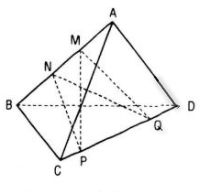
Hai đường thẳng MQ và NP chéo nhau.
Thật vậy, giả sử chúng không chéo nhau, tức chúng cùng thuộc một mp(αα) nào đó. Vậy M, N, P, Q cùng thuộc mp(αα) và do đó A, B, C, D cùng thuộc mp(α). Điều này mâu thuẫn với giả thiết ABCD là một tứ diện.
Chứng minh tương tự, hai đường thẳng MP và NQ cũng chéo nhau.
-- Mod Toán 11 HỌC247
-
Bài 2.12 trang 70 sách bài tập Hình học 11
bởi Mai Bảo Khánh
10/10/2018
Bài 2.12 (Sách bài tập - trang 70)Cho tứ diện ABCD. Cho I và J tương ứng là trung điểm của BC và AC, M là một điểm tùy y trên cạnh AD
a) Tìm giao tuyến d của hai mặt phẳng (MIJ) và (ABD)
b) Gọi N là giao điểm của BD với giao tuyến d, K là giao điểm của IN và JM. Tìm tập hợp điểm K khi M di động trên đoạn AD (M không phải là trung điểm của AD)
c) Tìm giao tuyến của hai mặt phẳng (ABK) và (MIJ)
Theo dõi (0) 1 Trả lời -
Bài 2.10 trang 70 sách bài tập Hình học 11
bởi Lê Văn Duyệt
10/10/2018
Bài 2.10 (Sách bài tập - trang 70)Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Tìm giao tuyến của các cặp mặt phẳng sau đây :
a) (SAC) và (SBD)
b) (SAB) và (SCD)
c) (SAD) và (SBC)
Theo dõi (0) 1 Trả lời -
CM đt đi qua G và 1 đỉnh của tứ diện sẽ đi qua trọng tâm của mặt đối diện với đỉnh ấy
bởi Thùy Trang
10/10/2018
gọi G là trọng tâm của tứ diện ABCD .
a) chứng minh rằng đường thẳng đi qua G và 1 đỉnh của tứ diện sẽ đi qua trọng tâm của mặt đối diện với đỉnh ấy .
b) gọi A' là trọng tâm của mặt BCD . chứng mình rằng GA=3GA' .
Theo dõi (0) 1 Trả lời
