Hoạt động khám phá 1 trang 66 SGK Toán 10 Chân trời sáng tạo tập 1
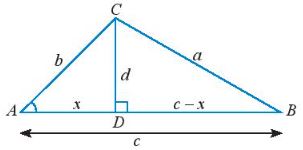
a) Cho tam giác ABC không phải là tam giác vuông với góc A nhọn và \(\widehat C \ge \widehat B.\) Vẽ đường cao CD và đặt tên các độ dài như trong Hình 1.
Hãy thay ? bằng các chữ cáu thích hợp để chứng minh công thức \({a^2} = {b^2} + {c^2} - 2bc\cos A\) theo gợi ý sau:
Xét tam giác vuông BCD, ta có: \({a^2} = {d^2} + {(c - x)^2} = {d^2} + {x^2} + {c^2} - 2xc\) (1)
Xét tam giác vuông ACD, ta có: \({b^2} = {d^2} + {x^2} \Rightarrow {d^2} = {b^2} - {x^2}\) (2)
\(\cos A = \frac{?}{b} \Rightarrow ? = b\cos A.\) (3)
Thay (2) và (3) vào (1), ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Lưu ý: Nếu \(\widehat B > \widehat C\) thì ta vẽ đường cao BD và chứng minh tương tự.
b) Cho tam giác ABC với góc A tù. Làm tương tự như trên, chứng minh rằng ta cũng có:
\({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Lưu ý: Vì A là góc tù nên \(\cos A = - \frac{x}{b}.\)
c) Cho tam giác ABC vuông tại A. Hãy chứng tỏ coogn thức \({a^2} = {b^2} + {c^2} - 2bc\cos A\) có thể viết là \({a^2} = {b^2} + {c^2}.\)
Hướng dẫn giải chi tiết Hoạt động khám phá 1
Phương pháp giải
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc\cos A\\{b^2} = {c^2} + {a^2} - 2ca\cos B\\{c^2} = {a^2} + {b^2} - 2ab\cos C\end{array}\)
Lời giải chi tiết
a) ? = x vì \(\cos A = \frac{{AD}}{{AC}} = \frac{x}{b} \Rightarrow ? = x.\)
b) Xét tam giác vuông BCD, ta có: \({a^2} = {d^2} + {(c + x)^2} = {d^2} + {x^2} + {c^2} + 2xc\) (1)
Xét tam giác vuông ACD, ta có: \({b^2} = {d^2} + {x^2} \Rightarrow {d^2} = {b^2} - {x^2}\) (2)
\(\cos A = - \cos \widehat {DAC} = - \frac{x}{b} \Rightarrow x = - b\cos A.\) (3)
Thay (2) và (3) vào (1), ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
c) Ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Mà \(\widehat A = {90^o} \Rightarrow \cos A = \cos {90^o} = 0.\)
\( \Rightarrow {a^2} = {b^2} + {c^2}\)
-- Mod Toán 10 HỌC247
-


Cho biết tam giác ABC có a = 7cm, b = 8cm, c = 6cm. Hãy tính độ dài đường trung tuyến ma của tam giác ABC đã cho.
bởi Nguyễn Thị Lưu
 29/08/2022
Theo dõi (0) 1 Trả lời
29/08/2022
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Hoạt động khởi động trang 65 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 1 trang 67 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng 1 trang 67 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 2 trang 67 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 69 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng 2 trang 69 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 3 trang 70 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 4 trang 70 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 71 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng 3 trang 72 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 72 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 72 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 72 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 74 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 74 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST