Giải bài 1 trang 74 SBT Toán 10 Chân trời sáng tạo tập 1
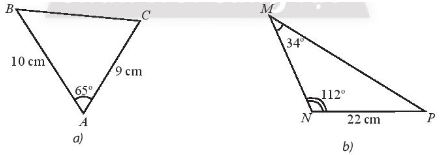
Tính độ dài các cạnh chưa biết trong các tam giác sau:
Hướng dẫn giải chi tiết Bài 1
Phương pháp giải
Áp dụng định lí côsin, sin:
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc\cos A\\{b^2} = {c^2} + {a^2} - 2ca\cos B\\{c^2} = {a^2} + {b^2} - 2ab\cos C\end{array}\)
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R.\)
(R là bán kính đường tròn ngoại tiếp tam giác ABC)
Lời giải chi tiết
a) Sử dụng định lí côsin ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos A\\ = {10^2} + {9^2} - 2.10.9.\cos 65^\circ \simeq 104,93\\ \Rightarrow BC \simeq \sqrt {104,96} \simeq 10,24\end{array}\)
b) Ta có: \(\widehat M + \widehat N + \widehat P = 180^\circ \Rightarrow \widehat P = 180^\circ - \widehat M - \widehat N = 180^\circ - 34^\circ - 112^\circ = 34^\circ \)
Áp dụng định lí sin ta có:
\(\begin{array}{l}\frac{{MN}}{{\sin P}} = \frac{{MP}}{{\sin N}} = \frac{{NP}}{{\sin M}} = 2R\\ \Leftrightarrow \frac{{MN}}{{\sin 34^\circ }} = \frac{{MP}}{{\sin 112^\circ }} = \frac{{22}}{{\sin 34^\circ }} \simeq 30,34\end{array}\)
\( \Rightarrow MN = 22,MP \simeq 36,48\) (cm)
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 9 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 74 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST