HŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo ChŲ░ŲĪng 4 B├Āi 2 ─Éß╗ŗnh l├Ł cosin v├Ā ─æß╗ŗnh l├Ł sin gi├║p c├Īc em hß╗Źc sinh nß║»m vß╗»ng phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp v├Ā ├┤n luyß╗ćn tß╗æt kiß║┐n thß╗®c.
-
Hoß║Īt ─æß╗Öng khß╗¤i ─æß╗Öng trang 65 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
L├Ām thß║┐ n├Āo ─æß╗ā t├Łnh ─æß╗Ö d├Āi cß║Īnh chŲ░a biß║┐t cß╗¦a hai tam gi├Īc dŲ░ß╗øi ─æ├óy?
-
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 1 trang 66 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
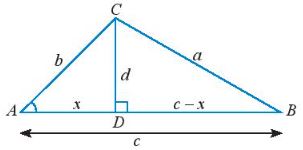
a) Cho tam gi├Īc ABC kh├┤ng phß║Żi l├Ā tam gi├Īc vu├┤ng vß╗øi g├│c A nhß╗Źn v├Ā \(\widehat C \ge \widehat B.\) Vß║Į ─æŲ░ß╗Øng cao CD v├Ā ─æß║Ęt t├¬n c├Īc ─æß╗Ö d├Āi nhŲ░ trong H├¼nh 1.
H├Ży thay ? bß║▒ng c├Īc chß╗» c├Īu th├Łch hß╗Żp ─æß╗ā chß╗®ng minh c├┤ng thß╗®c \({a^2} = {b^2} + {c^2} - 2bc\cos A\) theo gß╗Żi ├Į sau:
X├®t tam gi├Īc vu├┤ng BCD, ta c├│: \({a^2} = {d^2} + {(c - x)^2} = {d^2} + {x^2} + {c^2} - 2xc\) (1)
X├®t tam gi├Īc vu├┤ng ACD, ta c├│: \({b^2} = {d^2} + {x^2} \Rightarrow {d^2} = {b^2} - {x^2}\) (2)
\(\cos A = \frac{?}{b} \Rightarrow ? = b\cos A.\) (3)
Thay (2) v├Ā (3) v├Āo (1), ta c├│: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
LŲ░u ├Į: Nß║┐u \(\widehat B > \widehat C\) th├¼ ta vß║Į ─æŲ░ß╗Øng cao BD v├Ā chß╗®ng minh tŲ░ŲĪng tß╗▒.
b) Cho tam gi├Īc ABC vß╗øi g├│c A t├╣. L├Ām tŲ░ŲĪng tß╗▒ nhŲ░ tr├¬n, chß╗®ng minh rß║▒ng ta c┼®ng c├│:
\({a^2} = {b^2} + {c^2} - 2bc\cos A\)
LŲ░u ├Į: V├¼ A l├Ā g├│c t├╣ n├¬n \(\cos A = - \frac{x}{b}.\)
c) Cho tam gi├Īc ABC vu├┤ng tß║Īi A. H├Ży chß╗®ng tß╗Å coogn thß╗®c \({a^2} = {b^2} + {c^2} - 2bc\cos A\) c├│ thß╗ā viß║┐t l├Ā \({a^2} = {b^2} + {c^2}.\)
-
Thß╗▒c h├Ānh 1 trang 67 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
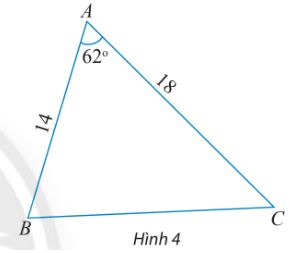
T├Łnh c├Īc cß║Īnh v├Ā c├Īc g├│c chŲ░a biß║┐t cß╗¦a tam gi├Īc ABC trong h├¼nh 4.
-
Vß║Łn dß╗źng 1 trang 67 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
T├Łnh khoß║Żng c├Īch giß╗»a hai ─æiß╗ām ß╗¤ hai ─æß║¦u cß╗¦a mß╗Öt hß╗ō nŲ░ß╗øc. Biß║┐t tß╗½ mß╗Öt ─æiß╗ām c├Īch hai ─æß║¦u hß╗ō lß║¦n lŲ░ß╗Żt l├Ā 800 m v├Ā 900 m ngŲ░ß╗Øi quan s├Īt nh├¼n hai ─æiß╗ām n├Āy dŲ░ß╗øi mß╗Öt g├│c \({70^o}\) (H├¼nh 5).
-
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 2 trang 67 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
a) Cho tam gi├Īc ABC kh├┤ng phß║Żi l├Ā tam gi├Īc vu├┤ng c├│ \(BC = a,AC = b,AB = c\) v├Ā R l├Ā b├Īn k├Łnh cß╗¦a ─æŲ░ß╗Øng trong ngoß║Īi tiß║┐p tam gi├Īc ─æ├│. Vß║Į ─æŲ░ß╗Øng k├Łnh BD.
i) T├Łnh \(\sin \widehat {BDC}\) theo a v├Ā R.
ii) T├¼m mß╗æi li├¬n hß╗ć giß╗»a hai g├│c \(\widehat {BAC}\) v├Ā \(\widehat {BDC}\). Tß╗½ ─æ├│ chß╗®ng minh rß║▒ng \(2R = \frac{a}{{\sin A}}.\)
b) Cho tam gi├Īc ABC vß╗øi g├│c A vu├┤ng. T├Łnh sinA v├Ā so s├Īnh a vß╗øi 2R ─æß╗ā chß╗®ng tß╗Å ta vß║½n c├│ c├┤ng thß╗®c \(2R = \frac{a}{{\sin A}}.\)
-
Thß╗▒c h├Ānh 2 trang 69 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
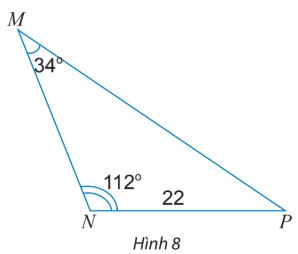
T├Łnh c├Īc cß║Īnh v├Ā c├Īc g├│c chŲ░a biß║┐t cß╗¦a tam gi├Īc MNP trong H├¼nh 8.
-
Vß║Łn dß╗źng 2 trang 69 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
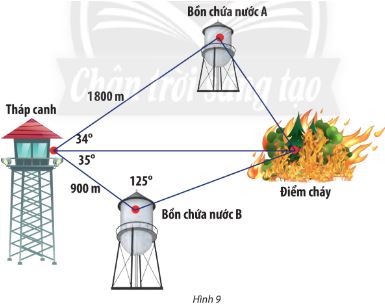
Trong mß╗Öt khu bß║Żo tß╗ōn, ngŲ░ß╗Øi ta x├óy dß╗▒ng mß╗Öt th├Īp canh v├Ā hai bß╗ōn chß╗®a nŲ░ß╗øc A, B ─æß╗ā ph├▓ng hß╗Åa hoß║Īn. Tß╗½ th├Īp canh, ngŲ░ß╗Øi ta ph├Īt hiß╗ćn ─æ├Īm ch├Īy v├Ā sß╗æ liß╗ću ─æŲ░a vß╗ü nhŲ░ H├¼nh 9. N├¬n dß║½n nŲ░ß╗øc tß╗½ bß╗ōn chß╗®a A hay B ─æß╗ā dß║Łp tß║»t ─æ├Īm ch├Īy nhanh hŲĪn?
-
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 3 trang 70 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho tam gi├Īc ABC nhŲ░ H├¼nh 10.
a) Viß║┐t c├┤ng thß╗®c t├Łnh diß╗ćn t├Łch S cß╗¦a tam gi├Īc ABC theo a v├Ā \({h_a}\)
b) T├Łnh \({h_a}\) theo b v├Ā sinC.
c) D├╣ng hai kß║┐t quß║Ż tr├¬n ─æß╗ā chß╗®ng minh c├┤ng thß╗®c \(S = \frac{1}{2}ab\sin C\)
d) D├╣ng ─æß╗ŗnh l├Ł sin v├Ā kß║┐t quß║Ż ß╗¤ c├óu c) ─æß╗ā chß╗®ng minh c├┤ng thß╗®c \(S = \frac{{abc}}{{4R}}\)
-
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 4 trang 70 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho tam gi├Īc ABC c├│ BC = a, AC = b, AB = c v├Ā (I;r) l├Ā ─æŲ░ß╗Øng tr├▓n nß╗Öi tiß║┐p tam gi├Īc (H├¼nh 11).
a) T├Łnh diß╗ćn t├Łch c├Īc tam gi├Īc IBC, IAC, IAB theo r v├Ā a, b, c.
b) D├╣ng kß║┐t quß║Ż tr├¬n ─æß╗ā chß╗®ng minh c├┤ng thß╗®c t├Łnh diß╗ćn t├Łch tam gi├Īc ABC: \(S = \frac{{r(a + b + c)}}{2}\)
-
Thß╗▒c h├Ānh 3 trang 71 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
T├Łnh diß╗ćn t├Łch tam gi├Īc ABC v├Ā b├Īn k├Łnh ─æŲ░ß╗Øng tr├▓n ngoß║Īi tiß║┐p tam gi├Īc ABC trong c├Īc trŲ░ß╗Øng hß╗Żp sau:
a) C├Īc cß║Īnh \(b = 14,c = 35\) v├Ā \(\widehat A = {60^o}\)
b) C├Īc cß║Īnh \(a = 4,b = 5,c = 3\)
-
Vß║Łn dß╗źng 3 trang 72 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
T├Łnh diß╗ćn t├Łch mß╗Öt c├Īnh buß╗ōm h├¼nh tam gi├Īc. Biß║┐t c├Īch buß╗ōm ─æ├│ c├│ chiß╗üu d├Āi mß╗Öt cß║Īnh l├Ā 3,2 m v├Ā hai g├│c kß╗ü c├Īch ─æ├│ c├│ sß╗æ ─æo l├Ā \({48^o}\) v├Ā \({105^o}\) (H├¼nh 12).
-
Giß║Żi b├Āi 1 trang 72 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
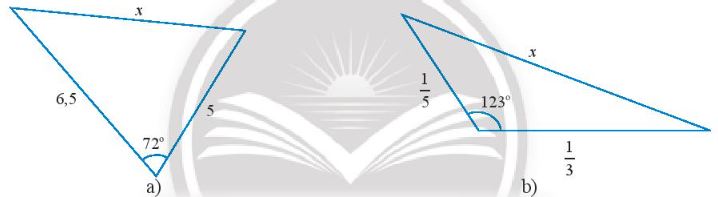
T├Łnh ─æß╗Ö d├Āi cß║Īnh x trong c├Īc tam gi├Īc sau:
-
Giß║Żi b├Āi 2 trang 72 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
T├Łnh ─æß╗Ö d├Āi cß║Īnh c trong tam gi├Īc ABC ß╗¤ H├¼nh 14.
-
Giß║Żi b├Āi 3 trang 72 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho tam gi├Īc ABC, biß║┐t cß║Īnh \(a = 152,\;\widehat B = {79^o},\;\widehat C = {61^o}.\) T├Łnh c├Īc g├│c, c├Īc cß║Īnh c├▓n lß║Īi v├Ā b├Īn k├Łnh ─æŲ░ß╗Øng tr├▓n ngoß║Īi tiß║┐p cß╗¦a tam gi├Īc ─æ├│.
-
Giß║Żi b├Āi 4 trang 73 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
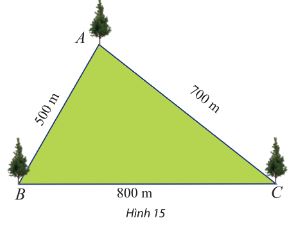
Mß╗Öt c├┤ng vi├¬n c├│ dß║Īng h├¼nh tam gi├Īc vß╗øi c├Īc k├Łch thŲ░ß╗øc nhŲ░ H├¼nh 15. T├Łnh sß╗æ ─æo c├Īc g├│c cß╗¦a tam gi├Īc ─æ├│.
-
Giß║Żi b├Āi 5 trang 73 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
T├Łnh diß╗ćn t├Łch mß╗Öt l├Ī cß╗Ø h├¼nh tam gi├Īc c├ón c├│ ─æß╗Ö d├Āi cß║Īnh b├¬n l├Ā 90 cm v├Ā g├│c ß╗¤ ─æß╗ēnh l├Ā \({35^o}.\)
-
Giß║Żi b├Āi 6 trang 73 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho tam gi├Īc ABC c├│ \(AB = 6,AC = 8\) v├Ā \(\widehat A = {60^o}.\)
a) T├Łnh diß╗ćn t├Łch tam gi├Īc ABC.
b) Gß╗Źi I l├Ā t├óm ─æŲ░ß╗Øng tr├▓n ngoß║Īi tiß║┐p tam gi├Īc ABC. T├Łnh diß╗ćn t├Łch tam gi├Īc IBC.
-
Giß║Żi b├Āi 7 trang 73 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho tam gi├Īc ABC c├│ trß╗Źng t├óm G v├Ā ─æß╗Ö d├Āi ba cß║Īnh AB, BC, CA lß║¦n lŲ░ß╗Żt l├Ā 15, 18, 27.
a) T├Łnh diß╗ćn t├Łch v├Ā b├Īn k├Łnh ─æŲ░ß╗Øng tr├▓n nß╗Öi tiß║┐p tam gi├Īc ABC.
b) T├Łnh diß╗ćn t├Łch tam gi├Īc GBC.
-
Giß║Żi b├Āi 8 trang 73 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho \({h_a}\) l├Ā ─æŲ░ß╗Øng cao vß║Į tß╗½ ─æß╗ēnh A, R l├Ā b├Īn k├Łnh ─æŲ░ß╗Øng tr├▓n ngoß║Īi tiß║┐p tam gi├Īc ABC. Chß╗®ng minh hß╗ć thß╗®c: \({h_a} = 2R\sin B\sin C.\)
-
Giß║Żi b├Āi 9 trang 73 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho tam gi├Īc ABC c├│ g├│c B nhß╗Źn, AD v├Ā CE l├Ā hai ─æŲ░ß╗Øng cao.
a) Chß╗®ng minh \(\frac{{{S_{BDE}}}}{{{S_{BAC}}}} = \frac{{BD.BE}}{{BA.BC}}.\)
b) Biß║┐t rß║▒ng \({S_{ABC}} = 9{S_{BDE}}\) v├Ā \(DE = 2\sqrt 2 .\) T├Łnh \(\cos B\) v├Ā b├Īn k├Łnh ─æŲ░ß╗Øng tr├▓n ngoß║Īi tiß║┐p tam gi├Īc ABC.
-
Giß║Żi b├Āi 10 trang 73 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho tß╗® gi├Īc lß╗ōi ABCD c├│ c├Īc ─æŲ░ß╗Øng ch├®o \(AC = x,BD = y\) v├Ā g├│c giß╗»a AC v├Ā BD bß║▒ng \(\alpha .\) Gß╗Źi S l├Ā diß╗ćn t├Łch cß╗¦a tß╗® gi├Īc ABCD.
a) Chß╗®ng minh \(S = \frac{1}{2}xy.\sin \alpha \)
b) N├¬u kß║┐t quß║Ż trong trŲ░ß╗Øng hß╗Żp \(AC \bot BD.\)
-
Giß║Żi b├Āi 1 trang 74 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
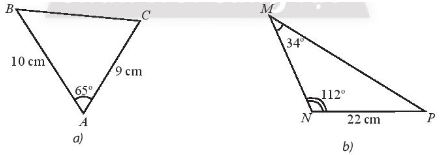
T├Łnh ─æß╗Ö d├Āi c├Īc cß║Īnh chŲ░a biß║┐t trong c├Īc tam gi├Īc sau:
-
Giß║Żi b├Āi 2 trang 74 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho tam gi├Īc ABC , biß║┐t cß║Īnh \(a = 75\) cm, \(\widehat B = 80^\circ ,\widehat C = 40^\circ \)
a) T├Łnh c├Īc g├│c, c├Īc cß║Īnh c├▓n lß║Īi cß╗¦a tam gi├Īc ABC
b) T├Łnh b├Īn k├Łnh ─æŲ░ß╗Øng tr├▓n ngoß║Īi tiß║┐p cß╗¦a tam gi├Īc ABC
-
Giß║Żi b├Āi 3 trang 75 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
T├Łnh g├│c lß╗øn nhß║źt cß╗¦a tam gi├Īc ABC, biß║┐t c├Īc cß║Īnh l├Ā \(a = 8,b = 12,c = 6\)
-
Giß║Żi b├Āi 4 trang 75 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
T├Łnh khoß║Żng c├Īch giß╗»a hai ─æiß╗ām P v├Ā Q cß╗¦a mß╗Öt hß╗ō nŲ░ß╗øc (h├¼nh 7). Cho biß║┐t tß╗½ mß╗Öt ─æiß╗ām O c├Īch hai ─æiß╗ām P v├Ā Q lß║¦n lŲ░ß╗Żt l├Ā 1400 m v├Ā 600 m ngŲ░ß╗Øi quan s├Īt nh├¼n thß║źy mß╗Öt g├│c \(76^\circ \)
-
Giß║Żi b├Āi 5 trang 75 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho tam gi├Īc ABC vß╗øi \(BC = a;AC = b;AB = c\). Chß╗®ng minh rß║▒ng:
\(1 + \cos A = \frac{{\left( {a + b + c} \right)\left( { - a + b + c} \right)}}{{2bc}}\)
-
Giß║Żi b├Āi 6 trang 75 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho tam gi├Īc ABC c├│ \(a = 24\)cm, \(b = 26\)cm, \(c = 30\)cm
a) T├Łnh diß╗ćn t├Łch tam gi├Īc ABC
b) T├Łnh b├Īn k├Łnh ─æŲ░ß╗Øng tr├▓n nß╗Öi tiß║┐p cß╗¦a tam gi├Īc ABC
-
Giß║Żi b├Āi 7 trang 75 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho tam gi├Īc MNP c├│ \(MN = 10,MP = 20\) v├Ā \(\widehat M = 42^\circ \)
a) T├Łnh diß╗ćn t├Łch tam gi├Īc MNP
b) Gß╗Źi O l├Ā t├óm ─æŲ░ß╗Øng tr├▓n ngoß║Īi tiß║┐p tam gi├Īc MNP. T├Łnh diß╗ćn t├Łch tam gi├Īc ONP
-
Giß║Żi b├Āi 8 trang 75 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho tam gi├Īc ABC c├│ trß╗Źng t├óm G. Chß╗®ng minh c├Īc tam gi├Īc GBC, GAB, GAC c├│ diß╗ćn t├Łch bß║▒ng nhau
-
Giß║Żi b├Āi 9 trang 75 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Cho tam gi├Īc ABC v├Ā c├│ c├Īc ─æiß╗ām BŌĆÖ, CŌĆÖ tr├¬n c├Īc cß║Īnh AB, AC. Chß╗®ng minh \(\frac{{{S_{ABC}}}}{{{S_{AB'C'}}}} = \frac{{AB.AC}}{{AB'.AC'}}\)
-
Giß║Żi b├Āi 10 trang 75 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
T├Łnh diß╗ćn t├Łch bß╗ü mß║Ęt cß╗¦a mß╗Öt miß║┐ng b├Īnh m├¼ kß║╣p kebab h├¼nh tam gi├Īc c├│ hai cß║Īnh lß║¦n lŲ░ß╗Żt l├Ā 10 cm, 12 cm v├Ā g├│c tß║Īo bß╗¤i hai cß║Īnh ─æ├│ l├Ā \(35^\circ \)

.JPG)