HŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 10 Kß║┐t nß╗æi tri thß╗®c ChŲ░ŲĪng 6 B├Āi 16 H├Ām sß╗æ bß║Łc hai gi├║p c├Īc em hß╗Źc sinh nß║»m vß╗»ng phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp v├Ā ├┤n luyß╗ćn tß╗æt kiß║┐n thß╗®c.
-
Hoß║Īt ─æß╗Öng 1 trang 11 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
X├®t b├Āi to├Īn r├Āo vŲ░ß╗Øn ß╗¤ t├¼nh huß╗æng mß╗¤ ─æß║¦u. Gß╗Źi x m├®t (0 < x < 10) l├Ā khoß║Żng c├Īch tß╗½ ─æiß╗ām cß║»m cß╗Źc ─æß║┐n bß╗Ø tŲ░ß╗Øng. H├Ży t├Łnh theo x:
a) ─Éß╗Ö d├Āi cß║Īnh PQ cß╗¦a mß║Żnh ─æß║źt.
b) Diß╗ćn t├Łch S(x) cß╗¦a mß║Żnh ─æß║źt ─æŲ░ß╗Żc r├Āo chß║»n.
-
C├óu hß╗Åi trang 12 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
H├Ām sß╗æ n├Āo dŲ░ß╗øi ─æ├óy l├Ā h├Ām sß╗æ bß║Łc hai?
A. \(y = x^{4}+3x^{2}+2\)
B. \(y=\frac{1}{x^{2}}\)
C. \(y=-3x^{2}+1\)
D. \(y = 3\left ( \frac{1}{x} \right )^{2}+3\frac{1}{x}-1\)
-
Luyß╗ćn tß║Łp 1 trang 12 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Cho h├Ām sß╗æ y = (x -1)(2 - 3x)
a) H├Ām sß╗æ ─æ├Ż cho c├│ phß║Żi l├Ā h├Ām sß╗æ bß║Łc hai kh├┤ng? Nß║┐u c├│, h├Ży x├Īc ─æß╗ŗnh c├Īc hß╗ć sß╗æ a, b, c cß╗¦a n├│.
b) Thay dß║źu ? bß║▒ng c├Īc sß╗æ th├Łch hß╗Żp ─æß╗ā ho├Ān th├Ānh bß║Żng gi├Ī trß╗ŗ sau cß╗¦a h├Ām sß╗æ ─æ├Ż cho.
-
Vß║Łn dß╗źng 1 trang 12 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Mß╗Öt vi├¬n bi rŲĪi tß╗▒ do tß╗½ ─æß╗Ö cao 19,6 m xuß╗æng mß║Ęt ─æß║źt. ─Éß╗Ö cao h (m├®t) so vß╗øi mß║Ęt ─æß║źt cß╗¦a vi├¬n bi trong khi rŲĪi phß╗ź thuß╗Öc v├Āo thß╗Øi gian t (giß║źy) theo c├┤ng thß╗®c: h = \(19,6-4,9t^{2}\); \(h, t\geq 0\).
a) Hß╗Åi sau bao nhi├¬u gi├óy kß╗ā tß╗½ khi rŲĪi vi├¬n bi chß║Īm ─æß║źt?
b) T├¼m tß║Łp x├Īc ─æß╗ŗnh v├Ā tß║Łp gi├Ī trß╗ŗ cß╗¦a h├Ām sß╗æ h.
-
Hoß║Īt ─æß╗Öng 2 trang 12 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
X├®t h├Ām sß╗æ \(y = S(x)=-2x^{2}+20x(0<x<10)\)
a) Tr├¬n mß║Ęt phß║│ng tß╗Źa ─æß╗Ö Oxy, biß╗āu diß║┐n tß╗Źa ─æß╗Ö c├Īc ─æiß╗ām trong bß║Żng gi├Ī trß╗ŗ cß╗¦a h├Ām sß╗æ lß║Łp ─æŲ░ß╗Żc ß╗¤ V├Ł dß╗ź 1. Nß╗æi c├Īc ─æiß╗ām ─æ├Ż vß║Į lß║Īi ta ─æŲ░ß╗Żc dß║Īng ─æß╗ō thß╗ŗ h├Ām sß╗æ \(y = S(x)=-2x^{2}+20x\) tr├¬n khoß║Żng (0;10) nhŲ░ trong h├¼nh 6.10. Dß║Īng ─æß╗ō thß╗ŗ cß╗¦a h├Ām sß╗æ \(y = S(x)=-2x^{2}+20x\) c├│ giß╗æng vß╗øi ─æß╗ō thß╗ŗ cß╗¦a h├Ām sß╗æ \(y = S(x)=-2x^{2}\) hay kh├┤ng?
b) Quan s├Īt dß║Īng ─æß╗ō thß╗ŗ cß╗¦a h├Ām sß╗æ \(y = S(x)=-2x^{2}+20x\) trong H├¼nh 6.10, t├¼m tß╗Źa ─æß╗Ö ─æiß╗ām cao nhß║źt cß╗¦a ─æß╗ō thß╗ŗ.
c) Thß╗▒c hiß╗ćn ph├®p biß║┐n ─æß╗Ģi \(y=-2x^{2}+20x=-2(x^{2}-10x)=-2(x^{2}-2.5.x+25)+50=-2(x-5)^{2}+50\)
H├Ży cho biß║┐t gi├Ī trß╗ŗ lß╗øn nhß║źt cß╗¦a diß╗ćn t├Łch mß║Żnh ─æß║źt ─æŲ░ß╗Żc r├Āo chß║»n. Tß╗½ ─æ├│ suy ra lß╗Øi giß║Żi cß╗¦a b├Āi to├Īn ß╗¤ phß║¦n mß╗¤ ─æß║¦u.
-
Hoß║Īt ─æß╗Öng 3 trang 13 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
TŲ░ŲĪng tß╗▒ H─É2, ta c├│ dß║Īng ─æß╗ō thß╗ŗ cß╗¦a mß╗Öt sß╗æ h├Ām sß╗æ bß║Łc hai sau:
Tß╗½ c├Īc ─æß╗ō thß╗ŗ h├Ām sß╗æ tr├¬n, h├Ży ho├Ān th├Ānh bß║Żng sau ─æ├óy:
-
Luyß╗ćn tß║Łp 2 trang 15 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Vß║Į parabol \(y=3x^{2}-10x+7\). Tß╗½ ─æ├│ t├¼m khoß║Żng ─æß╗ōng biß║┐n, nghß╗ŗch biß║┐n v├Ā gi├Ī trß╗ŗ nhß╗Å nhß║źt cß╗¦a h├Ām sß╗æ \(y=3x^{2}-10x+7\).
-
Vß║Łn dß╗źng 2 trang 15 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Bß║Īn Nam ─æß╗®ng dŲ░ß╗øi ch├ón cß║¦u vŲ░ß╗Żt ba tß║¦ng ß╗¤ n├║t giao ng├Ż ba Huß║┐, thuß╗Öc th├Ānh phß╗æ ─É├Ā Nß║Ąng ─æß╗ā ngß║»m cß║¦u vŲ░ß╗Żt. Biß║┐t rß║▒ng trß╗ź th├Īp dß║Īng ─æŲ░ß╗Øng parabol, khoß║Żng c├Īch giß╗»a hai ch├ón trß╗ź th├Īp khoß║Żng 27m, chiß╗üu cao cß╗¦a trß╗ź th├Īp t├Łnh tß╗½ ─æiß╗ām tr├¬n mß║Ęt ─æß║źt c├Īch ch├ón trß╗ź th├Īp 2,26m l├Ā 20m. H├Ży gi├║p bß║Īn Nam Ų░ß╗øc lŲ░ß╗Żng ─æß╗Ö cao cß╗¦a ─æß╗ēnh trß╗ź th├Īp cß║¦u (so vß╗øi mß║Ęt ─æß║źt).
-
Giß║Żi b├Āi 6.7 trang 16 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Vß║Į c├Īc ─æŲ░ß╗Øng parabol sau:
a) \(y=x^{2}-3x+2\)
b) \(y=-2x^{2}+2x+3\)
c) \(y=x^{2}+2x+1\)
d) \(y=-x^{2}+x-1\)
-
Giß║Żi b├Āi 6.8 trang 16 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Tß╗½ c├Īc parabol ─æ├Ż vß║Į ß╗¤ B├Āi tß║Łp 6.7 h├Ży cho biß║┐t khoß║Żng ─æß╗ōng biß║┐n v├Ā khoß║Żng nghß╗ŗch biß║┐n cß╗¦a mß╗æi h├Ām sß╗æ bß║Łc hai tŲ░ŲĪng ß╗®ng.
-
Giß║Żi b├Āi 6.9 trang 16 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
X├Īc ─æß╗ŗnh parabol \(y = ax^{2}+bx+1\). trong mß╗Śi trŲ░ß╗Øng hß╗Żp sau:
a) ─Éi qua hai ─æiß╗ām A(1; 0) v├Ā B(2; 4)
b) ─Éi qua ─æiß╗ām A(1; 0) v├Ā c├│ trß╗źc ─æß╗æi xß╗®ng x =1
c) C├│ ─æß╗ēnh I(1; 2)
d) ─Éi qua ─æiß╗ām A(-1; 6) v├Ā c├│ tung ─æß╗Ö ─æß╗ēnh -0,25.
-
Giß║Żi b├Āi 6.10 trang 16 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
X├Īc ─æß╗ŗnh parabol \(y = ax^{2}+bx+1\), biß║┐t rß║▒ng parabol ─æ├│ ─æi qua ─æiß╗ām A(8; 0) v├Ā c├│ ─æß╗ēnh l├Ā I(6; -12).
-
Giß║Żi b├Āi 6.11 trang 16 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Gß╗Źi (P) l├Ā ─æß╗ō thß╗ŗ h├Ām sß╗æ bß║Łc hai \(y = ax^{2}+bx+1\). H├Ży x├Īc ─æß╗ŗnh dß║źu cß╗¦a hß╗ć sß╗æ a v├Ā biß╗ćt thß╗®c \(\Delta \), trong mß╗Śi trŲ░ß╗Øng hß╗Żp sau:
a) (P) nß║▒m ho├Ān to├Ān ph├Ła tr├¬n trß╗źc ho├Ānh.
b) (P) nß║▒m ho├Ān to├Ān ph├Ła dŲ░ß╗øi trß╗źc ho├Ānh.
c) (P) cß║»t trß╗źc ho├Ānh tß║Īi hai ─æiß╗ām ph├ón biß╗ćt v├Ā c├│ ─æß╗ēnh nß║▒m ph├Ła dŲ░ß╗øi trß╗źc ho├Ānh.
d) (P) tiß║┐p x├║c vß╗øi trß╗źc ho├Ānh v├Ā nß║▒m ph├Ła tr├¬n trß╗źc ho├Ānh.
-
Giß║Żi b├Āi 6.12 trang 16 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Hai bß║Īn An v├Ā B├¼nh trao ─æß╗Ģi vß╗øi nhau:
An n├│i: Tß╗ø ─æß╗Źc ß╗¤ mß╗Öt t├Āi liß╗ću thß║źy n├│i rß║▒ng cß╗Ģng TrŲ░ß╗Øng ─Éß║Īi hß╗Źc B├Īch khoa H├Ā Nß╗Öi c├│ dß║Īng mß╗Öt parabol, khoß║Żng c├Īch giß╗»a hai ch├ón cß╗Ģng l├Ā 8m v├Ā chiß╗üu cao cß╗¦a cß╗Ģng t├Łnh tß╗½ mß╗Öt ─æiß╗ām tr├¬n mß║Ęt ─æß║źt c├Īch ch├ón cß╗Ģng l├Ā 0,5 m l├Ā 2,93 m. Tß╗½ ─æ├│ tß╗ø t├Łnh ra ─æŲ░ß╗Żc chiß╗üu cao cß╗¦a cß╗Ģng parabol ─æ├│ l├Ā 12m.
Sau mß╗Öt hß╗ōi suy ngh─®, B├¼nh n├│i: Nß║┐u dß╗» kiß╗ćn nhŲ░ bß║Īn n├│i, th├¼ chiß╗üu cao cß╗¦a cß╗Ģng parabol m├Ā bß║Īn t├Łnh ra ß╗¤ tr├¬n l├Ā kh├┤ng ch├Łnh x├Īc.
Dß╗▒a v├Āo th├┤ng tin m├Ā An ─æß╗Źc ─æŲ░ß╗Żc, em h├Ży t├Łnh chiß╗üu cao cß╗¦a cß╗Ģng TrŲ░ß╗Øng ─Éß║Īi hß╗Źc B├Īch Khoa H├Ā Nß╗Öi ─æß╗ā xem kß║┐t quß║Ż bß║Īn An t├Łnh ─æŲ░ß╗Żc c├│ ch├Łnh x├Īc kh├┤ng nh├®.
-
Giß║Żi b├Āi 6.13 trang 16 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
B├Īc H├╣ng d├╣ng 40 m lŲ░ß╗øi th├®p gai r├Āo th├Ānh mß╗Öt mß║Żnh vŲ░ß╗Øn h├¼nh chß╗» nhß║Łt ─æß╗ā trß╗ōng rau.
a) T├Łnh diß╗ćn t├Łch mß║Żnh vŲ░ß╗Øn h├¼nh chß╗» nhß║Łt r├Āo ─æŲ░ß╗Żc theo chiß╗üu rß╗Öng x (m├®t) cß╗¦a n├│.
b) T├¼m k├Łch thŲ░ß╗øc cß╗¦a mß║Żnh vŲ░ß╗Øn h├¼nh chß╗» nhß║Łt c├│ diß╗ćn t├Łch lß╗øn nhß║źt m├Ā b├Īc H├╣ng c├│ thß╗ā r├Āo ─æŲ░ß╗Żc.
-
Giß║Żi b├Āi 6.14 trang 16 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Quß╗╣ ─æß║Īo cß╗¦a mß╗Öt vß║Łt ─æŲ░ß╗Żc n├®m l├¬n tß╗½ gß╗æc O (─æŲ░ß╗Żc chß╗Źn l├Ā ─æiß╗ām n├®m) trong mß║Ęt phß║│ng tß╗Źa ─æß╗Ö Oxy l├Ā mß╗Öt parabol c├│ phŲ░ŲĪng tr├¼nh \(y=\frac{-3}{1000}x^{2}+x\), trong ─æ├│ x (m├®t) l├Ā khoß║Żng c├Īch theo phŲ░ŲĪng ngang tr├¬n mß║Ęt ─æß║źt tß╗½ vß╗ŗ tr├Ł cß╗¦a vß║Łt ─æß║┐n gß╗æc O, y (m├®t) l├Ā ─æß╗Ö cao cß╗¦a vß║Łt so vß╗øi mß║Ęt ─æß║źt
a) T├¼m ─æß╗Ö cao cß╗▒c ─æß║Īi cß╗¦a vß║Łt trong qu├Ī tr├¼nh bay.
b) T├Łnh khoß║Żng c├Īch tß╗½ ─æiß╗ām chß║Īm ─æß║źt sau khi bay cß╗¦a vß║Łt ─æß║┐n gß╗æc O. Khoß║Żng c├Īch n├Āy gß╗Źi l├Ā tß║¦m xa cß╗¦a quß╗╣ ─æß║Īo.
-
Giß║Żi b├Āi 6.11 trang 13 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Cho ─æß╗ō thß╗ŗ cß╗¦a hai h├Ām sß╗æ bß║Łc hai nhŲ░ dŲ░ß╗øi ─æ├óy
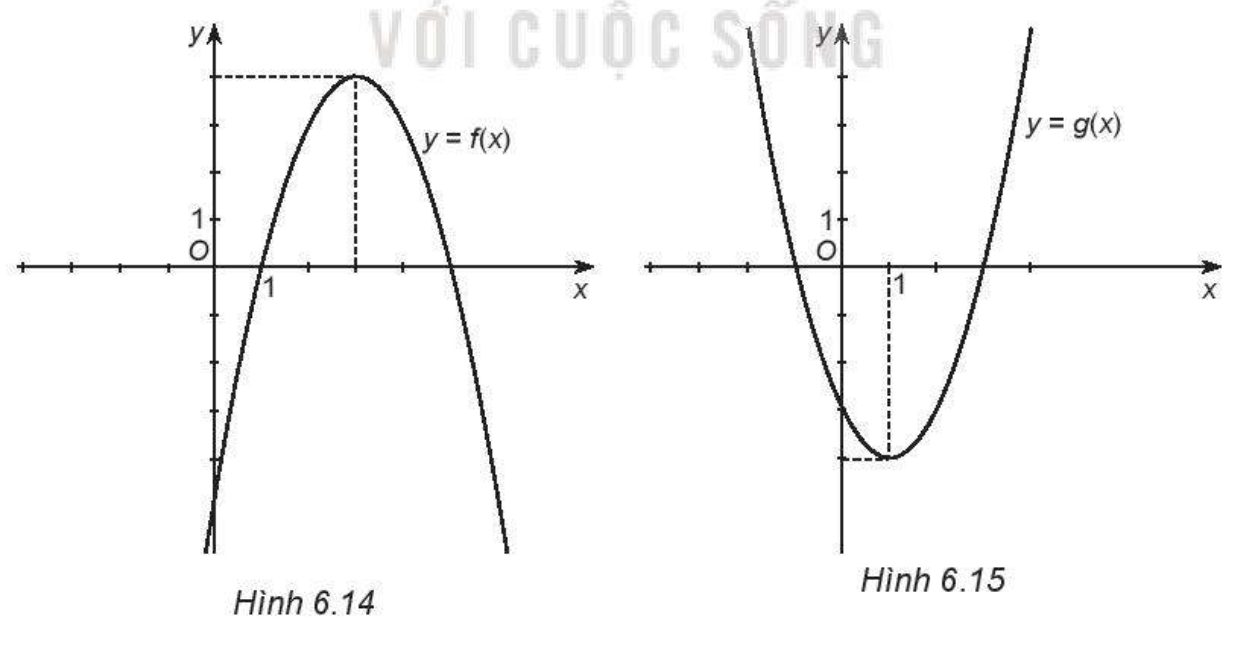
Vß╗øi mß╗Śi ─æß╗ō thß╗ŗ, h├Ży:
a) T├¼m tß╗Źa ─æß╗Ö ─æß╗ēnh cß╗¦a ─æß╗ō thß╗ŗ
b) T├¼m khoß║Żng ─æß╗ōng biß║┐n v├Ā khoß║Żng nghß╗ŗch biß║┐n cß╗¦a h├Ām sß╗æ
c) T├¼m gi├Ī trß╗ŗ lß╗øn nhß║źt hoß║Ęc gi├Ī trß╗ŗ nhß╗Å nhß║źt cß╗¦a h├Ām sß╗æ
d) T├¼m tß║Łp x├Īc ─æß╗ŗnh v├Ā tß║Łp gi├Ī trß╗ŗ cß╗¦a h├Ām sß╗æ
-
Giß║Żi b├Āi 6.12 trang 14 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Vß╗øi mß╗Śi h├Ām sß╗æ bß║Łc hai cho dŲ░ß╗øi ─æ├óy: \(y = f(x) = - {x^2} - x + 1\); \(y = g(x) = {x^2} - 8x + 8\)
H├Ży thß╗▒c hiß╗ćn c├Īc y├¬u cß║¦u sau:
a) Viß║┐t lß║Īi h├Ām sß╗æ bß║Łc hai dŲ░ß╗øi dß║Īng \(y = a{(x - h)^2} + k\)
b) T├¼m gi├Ī trß╗ŗ lß╗øn nhß║źt hoß║Ęc gi├Ī trß╗ŗ nhß╗Å nhß║źt cß╗¦a h├Ām sß╗æ
c) Vß║Į ─æß╗ō thß╗ŗ cß╗¦a h├Ām sß╗æ
-
Giß║Żi b├Āi 6.13 trang 14 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
T├¼m tß║Łp x├Īc ─æß╗ŗnh v├Ā tß║Łp gi├Ī trß╗ŗ cß╗¦a c├Īc h├Ām sß╗æ bß║Łc hai sau:
a) \(f(x) = - {x^2} + 4x - 3\)
b) \(f(x) = {x^2} - 7x + 12\)
-
Giß║Żi b├Āi 6.14 trang 14 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Tìm parabol \(y = a{x^2} + bx + 2\), biết rằng parabol đó
a) ─Éi qua hai ─æiß╗ām \(M(1;5)\) v├Ā \(N( - 2;8)\)
b) ─Éi qua ─æiß╗ām \(A(3; - 4)\) v├Ā c├│ trß╗źc ─æß╗æi xß╗®ng \(x = - \frac{3}{2}\)
c) C├│ ─æß╗ēnh \(I(2; - 2)\)
-
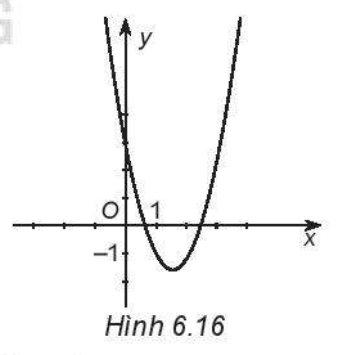
Giß║Żi b├Āi 6.16 trang 14 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
X├Īc ─æß╗ŗnh dß║źu cß╗¦a c├Īc hß╗ć sß╗æ a, b, c v├Ā dß║źu cß╗¦a biß╗ćt thß╗®c \(\Delta = {b^2} - 4ac\) cß╗¦a h├Ām sß╗æ bß║Łc hai \(y = a{x^2} + bx + c\), biß║┐t ─æß╗ō thß╗ŗ cß╗¦a n├│ c├│ dß║Īng nhŲ░ H├¼nh 6.16.
-
Giß║Żi b├Āi 6.17 trang 14 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
B├Īc H├╣ng d├╣ng 200 m h├Āng r├Āo d├óy th├®p gai ─æß╗ā r├Āo miß║┐ng ─æß║źt ─æß╗¦ rß╗Öng th├Ānh mß╗Öt mß║Żnh vŲ░ß╗Øn h├¼nh chß╗» nhß║Łt.
a) T├¼m c├┤ng thß╗®c t├Łnh diß╗ćn t├Łch S(x) cß╗¦a mß║Żnh vŲ░ß╗Øn h├¼nh chß╗» nhß║Łt r├Āo ─æŲ░ß╗Żc theo chiß╗üu rß╗Öng x (m) cß╗¦a mß║Żnh vŲ░ß╗Øn ─æ├│
b) T├¼m k├Łch thŲ░ß╗øc cß╗¦a mß║Żnh vŲ░ß╗Øn h├¼nh chß╗» nhß║Łt c├│ diß╗ćn t├Łch lß╗øn nhß║źt c├│ thß╗ā r├Āo ─æŲ░ß╗Żc.
-
Giß║Żi b├Āi 6.18 trang 15 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Mß╗Öt quß║Ż b├│ng ─æŲ░ß╗Żc n├®m l├¬n tr├¬n theo phŲ░ŲĪng thß║│ng ─æß╗®ng tß╗½ mß║Ęt ─æß║źt vß╗øi vß║Łn tß╗æc ban ─æß║¦u 14,7 m/s. Khi bß╗Å qua sß╗®c cß║Żn cß╗¦a kh├┤ng kh├Ł, ─æß╗Ö cao cß╗¦a quß║Ż b├│ng so vß╗øi mß║Ęt ─æß║źt (t├Łnh bß║▒ng m├®t) c├│ thß╗ā m├┤ tß║Ż bß╗¤i PT:
\(h(t) = - 4,9{t^2} + 14,7t\)
a) Sau khi n├®m bao nhi├¬u gi├óy th├¼ quß║Ż b├│ng ─æß║Īt ─æß╗Ö cao lß╗øn nhß║źt?
b) T├¼m ─æß╗Ö cao lß╗øn nhß║źt cß╗¦a quß║Ż b├│ng
c) Sau khi n├®m bao nhi├¬u gi├óy th├¼ quß║Ż b├│ng rŲĪi chß║Īm ─æß║źt?
-
Giß║Żi b├Āi 6.19 trang 15 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Mß╗Öt h├▓n ─æ├Ī ─æŲ░ß╗Żc n├®m l├¬n tr├¬n theo phŲ░ŲĪng thß║│ng ─æß╗®ng. Khi bß╗Å qua sß╗®c cß║Żn cß╗¦a kh├┤ng kh├Ł, chuyß╗ān ─æß╗Öng cß╗¦a h├▓n ─æ├Ī tu├ón theo phŲ░ŲĪng tr├¼nh sau:
\(y = - 4,9{t^2} + mt + n\)
vß╗øi m, n l├Ā c├Īc hß║▒ng sß╗æ. ß╗× ─æ├óy t = 0 l├Ā thß╗Øi ─æiß╗ām h├▓n ─æ├Ī ─æŲ░ß╗Żc n├®m l├¬n, y(t) l├Ā ─æß╗Ö cao cß╗¦a h├▓n ─æ├Ī tß║Īi thß╗Øi ─æiß╗ām t (gi├óy) sau khi n├®m v├Ā y = 0 ß╗®ng vß╗øi b├│ng chß║Īm ─æß║źt.
a) T├¼m phŲ░ŲĪng tr├¼nh chuyß╗ān ─æß╗Öng cß╗¦a h├▓n ─æ├Ī, biß║┐t rß║▒ng ─æiß╗ām n├®m c├Īch mß║Ęt ─æß║źt 1,5 m v├Ā thß╗Øi gian ─æß╗ā h├▓n ─æ├Ī ─æß║Īt ─æß╗Ö cao lß╗øn nhß║źt l├Ā 1,2 gi├óy sau khi n├®m
b) T├¼m ─æß╗Ö cao cß╗¦a h├▓n ─æ├Ī sau 2 gi├óy kß╗ā tß╗½ khi bß║»t ─æß║¦u n├®m
c) Sau bao l├óu kß╗ā tß╗½ khi n├®m, h├▓n ─æ├Ī rŲĪi xuß╗æng mß║Ęt ─æß║źt (Kß║┐t quß║Ż l├Ām tr├▓n ─æß║┐n chß╗» sß╗æ thß║Łp ph├ón thß╗® hai)?
-
Giß║Żi b├Āi 6.20 trang 15 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 2 - KNTT
Mß╗Öt rß║Īp chiß║┐u phim c├│ sß╗®c chß╗®a 1 000 ngŲ░ß╗Øi. Vß╗øi gi├Ī v├® l├Ā 40 000 ─æß╗ōng, trung b├¼nh sß║Į c├│ khoß║Żng 300 ngŲ░ß╗Øi ─æß║┐n rß║Īp xem phim mß╗Śi ng├Āy. ─Éß╗ā t─āng sß╗æ lŲ░ß╗Żng v├® b├Īn ra, rß║Īp chiß║┐u phim ─æ├Ż kh├Īo s├Īt thß╗ŗ trŲ░ß╗Øng v├Ā thß║źy rß║▒ng nß║┐u gi├Ī v├® cß╗® giß║Żm 10 000 ─æß╗ōng th├¼ sß║Į c├│ th├¬m 100 ngŲ░ß╗Øi ─æß║┐n xem phim mß╗Śi ng├Āy.
a) T├¼m c├┤ng thß╗®c cß╗¦a h├Ām sß╗æ R(x) m├┤ tß║Ż doanh thu tß╗½ tiß╗ün b├Īn v├® mß╗Śi ng├Āy cß╗¦a rß║Īp chiß║┐u phim khi gi├Ī v├® l├Ā x ngh├¼n ─æß╗ōng
b) T├¼m mß╗®c gi├Ī v├® ─æß╗ā doanh thu tß╗½ tiß╗ün b├Īn v├® mß╗Śi ng├Āy cß╗¦a rß║Īp l├Ā lß╗øn nhß║źt.

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)





