Giải bài 6.16 trang 14 SBT Toán 10 Kết nối tri thức tập 2
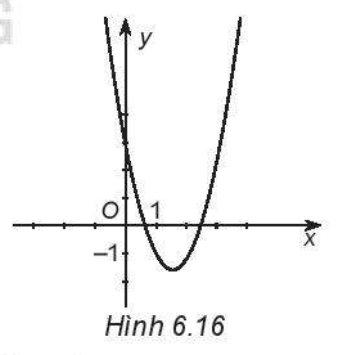
Xác định dấu của các hệ số a, b, c và dấu của biệt thức \(\Delta = {b^2} - 4ac\) của hàm số bậc hai \(y = a{x^2} + bx + c\), biết đồ thị của nó có dạng như Hình 6.16.
Hướng dẫn giải chi tiết Bài 6.16
Phương pháp giải
Bước 1: Dựa vào chiều bề lõm quay lên trên/ xuống dưới để tìm dấu của hệ số a
Bước 2: Xét dấu của tung độ giao điểm của ĐTHS với trục Oy để tìm dấu của hệ số c
Bước 3: Xét dấu tọa độ đỉnh của parabol để xét dấu các biểu thức \( - \frac{b}{{2a}}\) và \( - \frac{\Delta }{{4a}}\). Từ đó suy ra dấu của hệ số b và ∆
Lời giải chi tiết
- Do parabol có bề lõm quay lên trên nên a > 0
- ĐTHS cắt trục tung tại điểm có tung độ dương nên c > 0
- Đỉnh parabol có hoành độ dương, tung độ âm nên ta có \(\left\{ \begin{array}{l} - \frac{b}{{2a}} > 0\\ - \frac{\Delta }{{4a}} < 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b < 0\\\Delta > 0\end{array} \right.\) (do a > 0)
Vậy a > 0, b < 0, c > 0, ∆ > 0.
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 6.13 trang 14 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 6.14 trang 14 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 6.17 trang 14 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 6.18 trang 15 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 6.19 trang 15 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 6.20 trang 15 SBT Toán 10 Kết nối tri thức tập 2 - KNTT





