Giải bài 1.40 tr 42 SBT Hình học 10
a) Cho A(−1;8), B(1;6), C(3;4). Chứng minh ba điểm A, B, C thẳng hàng.
b) Cho A(1;1), B(3;2), C(m+4;2m+1). Tìm m để ba điểm A, B, C thẳng hàng.
Hướng dẫn giải chi tiết
a) \(\overrightarrow {AB} = \left( {2; - 2} \right);\overrightarrow {AC} = \left( {4; - 4} \right)\)
Vậy \(\overrightarrow {AC} = 2\overrightarrow {AB} \) ⇒ ba điểm A, B, C thẳng hàng.
b) \(\overrightarrow {AB} = \left( {2;1} \right);\overrightarrow {AC} = \left( {m + 3;2m} \right)\)
Ba điểm A, B, C thẳng hàng \( \Leftrightarrow \frac{{3m}}{2} = \frac{{2m}}{2} \Leftrightarrow m = 1\).
-- Mod Toán 10 HỌC247
-

 Cho tam giác ABC đều cạnh a. Chọn hệ tọa độ , trong đó O là trung điểm của cạnh BC, cùng hướng với , cùng hướng với : a) Tính tọa độ của các đỉnh của tam giác ABC b) Tìm tọa độ trung điểm E của AC c) Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABCTheo dõi (1) 0 Trả lời
Cho tam giác ABC đều cạnh a. Chọn hệ tọa độ , trong đó O là trung điểm của cạnh BC, cùng hướng với , cùng hướng với : a) Tính tọa độ của các đỉnh của tam giác ABC b) Tìm tọa độ trung điểm E của AC c) Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABCTheo dõi (1) 0 Trả lời -


Tìm tọa độ điểm M thỏa vtMA+2vtMB=vtAC
bởi Tân Ng
 10/10/2019
10/10/2019
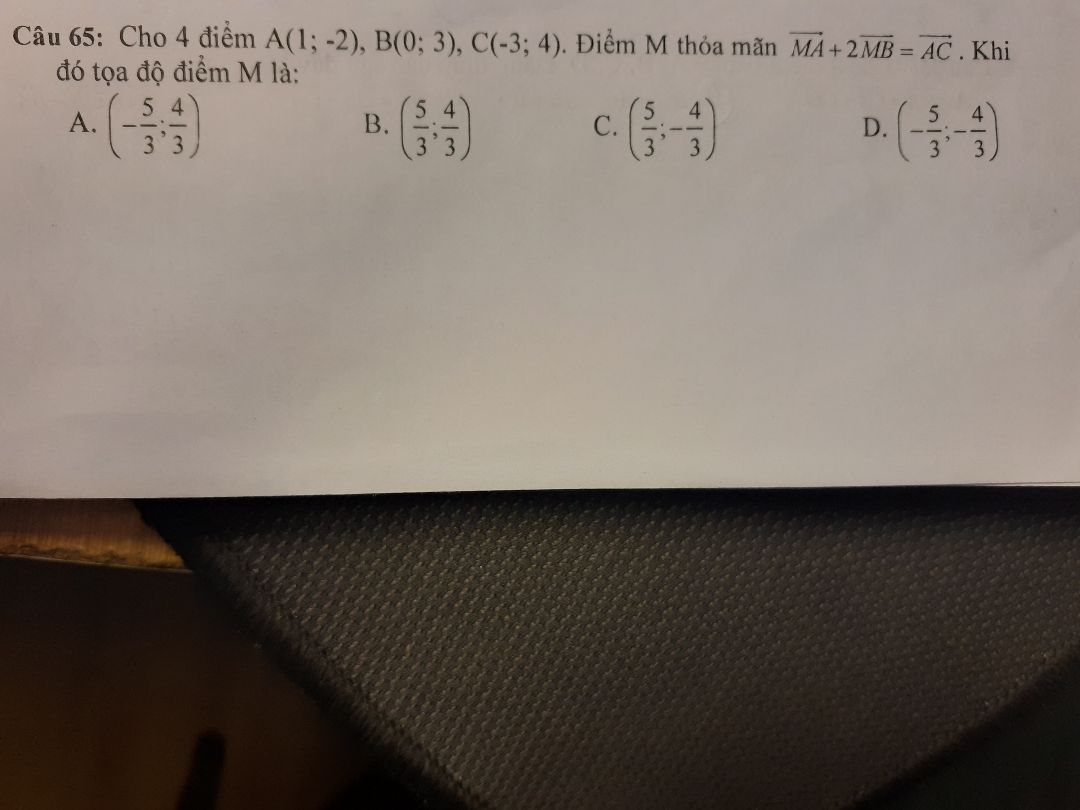 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Tìm toạ độ điểm D sao cho ABCD là hình bình hành biết A( -1;-2), B (3;2) , C(4;-1)
bởi Việt Hoàng
 04/10/2019
cho 3 điểm A( -1;-2) , B ( 3;2) , C(4;-1) . Tìm toạ độ điểm D sao cho ABCD là hình bình hành ; tìm toạ độ điểm E sao cho E đối xứng với B qua CTheo dõi (1) 0 Trả lời
04/10/2019
cho 3 điểm A( -1;-2) , B ( 3;2) , C(4;-1) . Tìm toạ độ điểm D sao cho ABCD là hình bình hành ; tìm toạ độ điểm E sao cho E đối xứng với B qua CTheo dõi (1) 0 Trả lời -

 Cho A ( -4 , 1) B ( 2 , 4 ) C ( 2 , -2 ) a: Chứng minh 3 điểm A,B,C không thẳng hàng b : Tính cos góc CBAc : Tính chu vi diện tích tam giác ABCTheo dõi (2) 0 Trả lời
Cho A ( -4 , 1) B ( 2 , 4 ) C ( 2 , -2 ) a: Chứng minh 3 điểm A,B,C không thẳng hàng b : Tính cos góc CBAc : Tính chu vi diện tích tam giác ABCTheo dõi (2) 0 Trả lời -


Chứng minh tam giác ABC cân tại A biết A( 4;6 ), B( 1;4 ), C( 7; 3/2 ).
bởi Phạm Phú Lộc Nữ
 13/10/2018
13/10/2018
Trong 1 mặt phẳng tọa độ Oxy cho A( 4;6 ), B( 1;4 ), C( 7; 3/2 ).
a, CMR tam giác ABC vuông tại A
b, Tìm độ dài trung tuyến CM
c, Tim tọa đọ trọng tâm của tam giác ABC
d, Tính chu vi và diện tích của tam giác ABC
e, tìm tọa độ điểm D để tứ giác ABCD là hình bình hành
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1.38 trang 42 SBT Hình học 10
Bài tập 1.39 trang 42 SBT Hình học 10
Bài tập 1.41 trang 42 SBT Hình học 10
Bài tập 1.42 trang 42 SBT Hình học 10
Bài tập 1.43 trang 42 SBT Hình học 10
Bài tập 1.44 trang 42 SBT Hình học 10
Bài tập 1.45 trang 42 SBT Hình học 10
Bài tập 1.46 trang 42 SBT Hình học 10
Bài tập 1.47 trang 42 SBT Hình học 10
Bài tập 29 trang 30 SGK Hình học 10 NC
Bài tập 30 trang 31 SGK Hình học 10 NC
Bài tập 31 trang 31 SGK Hình học 10 NC
Bài tập 32 trang 31 SGK Hình học 10 NC
Bài tập 33 trang 31 SGK Hình học 10 NC
Bài tập 34 trang 31 SGK Hình học 10 NC





