Bài tập 1.46 trang 42 SBT Hình học 10

28 BT SGK

Giải bài 1.46 tr 42 SBT Hình học 10

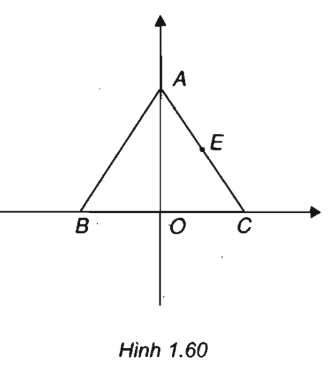
Cho tam giác đều ABC cạnh a. Chọn hệ tọa độ \(\left( {O;\overrightarrow i ;\overrightarrow j } \right)\), trong đó O là trung điểm của cạnh BC, \(\overrightarrow i \) cùng hướng với \(\overrightarrow {OC}\), \(\overrightarrow j\) cùng hướng với \(\overrightarrow {OA}\).

a) Tính tọa độ của các đỉnh của tam giác ABC.

b) Tìm tọa độ trung điểm E của AC.

c) Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC.

Hình học 10 Chương 1 Bài 4 Trắc nghiệm Hình học 10 Chương 1 Bài 4 Giải bài tập Hình học 10 Chương 1 Bài 4

Hướng dẫn giải chi tiết

Giải sách bài tập Toán 10 | Giải sbt Toán 10

a) Do O là trung điểm CB nên \(OB = OC = \frac{a}{2}\) và \(OA = \sqrt {A{C^2} - O{C^2}} = \sqrt {a - \frac{{{a^2}}}{4}} = \frac{{a\sqrt 3 }}{2}\)

Từ hình vẽ ta suy ra \(A\left( {0;\frac{{a\sqrt 3 }}{2}} \right),B\left( { - \frac{a}{2};0} \right),C\left( {\frac{a}{2};0} \right)\)

b) Do E là trung điểm của AC nên \(\left\{ \begin{array}{l}
{x_E} = \frac{{0 + \frac{a}{2}}}{2} = \frac{a}{4}\\
{y_E} = \frac{{\frac{{a\sqrt 3 }}{2} + 0}}{2} = \frac{{a\sqrt 3 }}{4}
\end{array} \right.\) hay \(E\left( {\frac{a}{4};\frac{{a\sqrt 3 }}{4}} \right)\)

c) Tâm đường tròn ngoại tiếp tam giác đều trùng với trọng tâm của tam giác.

Gọi G là trọng tâm tam giác thì \(\left\{ \begin{array}{l}
{x_G} = \frac{{0 + \left( { - \frac{a}{2}} \right) + \frac{a}{2}}}{3} = 0\\
{y_G} = \frac{{\frac{{a\sqrt 3 }}{2} + 0 + 0}}{3} = \frac{{a\sqrt 3 }}{6}
\end{array} \right.\) hay \(G\left( {0;\frac{{a\sqrt 3 }}{6}} \right)\)

-- Mod Toán 10 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 1.46 trang 42 SBT Hình học 10 HAY thì click chia sẻ

YOMEDIA

Bài 1.32 trang 34 sách bài tập Hình học 10

bởi hà trang 02/10/2018

Bài 1.32 (SBT trang 34)
Cho tứ giác ABCD. Gọi I và J lần lượt là trung điểm của hai đường chéo AC và BD. Chứng minh \(\overrightarrow{AB}+\overrightarrow{CD}=2\overrightarrow{IJ}\) ?

Theo dõi (0) 1 Trả lời
Bài 1.31 trang 34 sách bài tập Hình học 10

bởi Thùy Trang 02/10/2018

Bài 1.31 (SBT trang 34)
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Chứng minh rằng với điểm M bất kì ta có \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=4\overrightarrow{MO}\)

Theo dõi (0) 1 Trả lời
Bài 1.30 trang 34 sách bài tập Hình học 10

bởi Nguyễn Hạ Lan 02/10/2018

Bài 1.30 (SBT trang 34)
Cho tam giác ABC. Điểm I trên cạnh AC sao cho \(CI=\dfrac{1}{4}CA\). J là điểm mà \(\overrightarrow{BJ}=\dfrac{1}{2}\overrightarrow{AC}-\dfrac{3}{2}\overrightarrow{AB}\)

a) Chứng minh \(\overrightarrow{BI}=\dfrac{3}{4}\overrightarrow{AC}-\overrightarrow{AB}\)

b) Chứng minh B, I, J thẳng hàng

c) Hãy dựng điểm J thỏa mãn điều kiện đề bài

Theo dõi (0) 1 Trả lời
Bài 1.29 trang 34 sách bài tập Hình học 10

bởi Mai Bảo Khánh 02/10/2018

Bài 1.29 (SBT trang 34)
Cho tam giác ABC. Dựng \(\overrightarrow{AB'}=\overrightarrow{BC};\overrightarrow{CA'}=\overrightarrow{AB};\overrightarrow{BC'}=\overrightarrow{CA}\)

a) Chứng minh rằng A là trung điểm của B'C'

b) Chứng minh các đường thẳng \(AA';BB'\) và \(CC'\) đồng quy

Theo dõi (0) 1 Trả lời
Bài 1.28 trang 34 sách bài tập Hình học 10

bởi Thùy Nguyễn 02/10/2018

Bài 1.28 (SBT trang 34)
Cho tam giác ABC. Gọi M là trung điểm của AB và N là một điểm trên canh AC sao cho NA = 2NC. Gọi K là trung điểm của MN

Phân tích vectơ \(\overrightarrow{AK}\) theo \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\) ?

Theo dõi (0) 1 Trả lời