Toán 10 Cánh Diều Bài 4: Bất phương trình bậc hai một ẩn

Ví dụ: Cho bất phương trình bậc hai một ẩn \({x^2} - 4{\rm{x}} + 3 < 0(1)\). Trong các giá trị sau đây của x, giá trị nào là nghiệm của bất phương trình (1)?

a) x = 2;

b) x=0;

c) x = 4.

Giải

a) Với x=2, ta có: 2² - 4.2 + 3 = - 1 <0. Vậy x = 2 là nghiệm của bất phương trình (1).

b) Với x = 0, ta có: 0² - 4. 0 + 3 = 3 >0. Vậy x = 0 không phải là nghiệm của bất phương trình (1).

c) Với x= 3, ta có: 3² - 4. 3 + 3 = 0. Vậy x = 3 không phải là nghiệm của bất phương trình (1).

Chú ý: Giải bất phương trình bậc hai ẩn x là đi tìm tập nghiệm của bất phương trình đó.

* Giải bằng cách xét dấu tam thức bậc hai

Bước 1: Xác định dấu của a và tìm nghiệm của f(x) (nếu có)

Bước 2: Sử dụng định lí về dấu của tam thức bậc hai để tìm tập hợp những giá trị x sao cho f(x) thỏa mãn yêu cầu đề bài.

+ \(\Delta  < 0\): f(x) cùng dấu với a, \(\forall x \in \mathbb{R}\)

+ \(\Delta  = 0\): f(x) cùng dấu với a, \(\forall x \in \mathbb{R}{\rm{\backslash }}\left\{ {\frac{{ - b}}{{2a}}} \right\}\)

+ \(\Delta  < 0\): f(x) có 2 nghiệm \({x_1},{x_2}({x_1} < {x_2})\)

* Giải bằng cách sử dụng đồ thị

+) Nghiệm của BPT \(a{x^2} + bx + c > 0\) là tập hợp x ứng với phần Parabol \(y = a{x^2} + bx + c\) nằm phía trên trục hoành.

+) Nghiệm của BPT \(a{x^2} + bx + c < 0\) là tập hợp x ứng với phần Parabol \(y = a{x^2} + bx + c\) nằm phía dưới trục hoành.

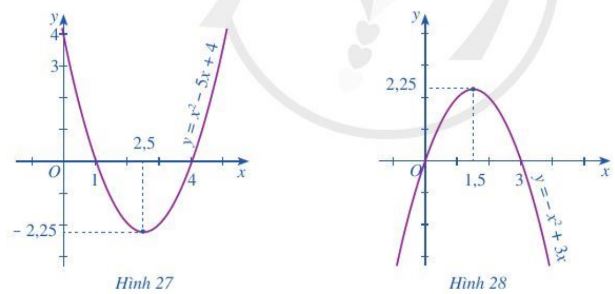
Ví dụ: Quan sát đồ thị ở Hình 27, Hình 28 và giải các bất phương trình bậc hai sau:

\(\begin{array}{l}
a){x^2} - 5x + 4 < 0\\
b) - {x^2} + 3x > 0
\end{array}\)

Giải

a) Quan sát đồ thị ở hình 27, ta thấy: \({x^2} - 5x + 4 < 0\) biểu diễn phần parabol \(y = {x^2} - 5x + 4\) nằm phía dưới trục hoành, tương ứng với 1 < x < 4.

Vậy tập nghiệm của bất phương trình \({x^2} - 5x + 4 < 0\) là khoảng (1 ; 4).

b) Quan sát đồ thị ở hình 28, ta thấy: \( - {x^2} + 3x > 0\) biểu diễn phần parabol \(y =  - {x^2} + 3x\) nằm phía trên trục hoành, tương ứng với 0 < x < 3. Vậy tập nghiệm của bất phương trình \( - {x^2} + 3x > 0\) là khoảng (0; 3).

Bất phương trình bậc hai một ẩn có nhiều ứng dụng, chẳng hạn: giải một số hệ bất phương trình; ứng dụng vào tính toán lợi nhuận trong kinh doanh; tính toán điểm rơi trong pháo binh; ...

Câu 1: Giải các bất phương trình bậc hai sau:

a) \(3{x^2} - 2x + 4 \le 0\)

b) \( - {x^2} + 6x - 9 \ge 0\)

Hướng dẫn giải

a) Ta có \(a = 3 > 0\) và tam thức bậc hai \(f\left( x \right) = 3{x^2} - 2x + 4\) có \(\Delta ' = {1^2} - 3.4 =  - 11 < 0\)

=> \(f\left( x \right) = 3{x^2} - 2x + 4\) vô nghiệm.

=> \(3{x^2} - 2x + 4 > 0\forall x \in \mathbb{R}\)

b) Ta có: \(a =  - 1 < 0\) và \(\Delta ' = {3^2} - \left( { - 1} \right).\left( { - 9} \right) = 0\)

=> \(f\left( x \right) =  - {x^2} + 6x - 9\) có nghiệm duy nhất \(x = 3\).

=> \( - {x^2} + 6x - 9 < 0\forall x \in \mathbb{R}\backslash \left\{ 3 \right\}\)

Câu 2: Giải mỗi bất phương trình bậc hai sau bằng cách sử dụng đồ thị:

a) \({x^2} + 2x + 2 > 0\)

b) \( - 3{x^2} + 2x - 1 > 0\)

Hướng dẫn giải

a) Ta có đồ thị:

Từ đồ thị ta thấy \({x^2} + 2x + 2 > 0\) biểu diễn phần parabol \(y = {x^2} + 2x + 2\) nằm phía trên trục hoành, tương ứng với mọi \(x \in \mathbb{R}\).

Vậy tập nghiệm của bất phương trình \({x^2} + 2x + 2 > 0\) là \(\mathbb{R}\).

b) Ta có đồ thị:

Từ đồ thị ta thấy \( - 3{x^2} + 2x - 1 > 0\) biểu diễn phần parabol \(y =  - 3{x^2} + 2x - 1\) nằm phía trên trục hoành, tương ứng với \(x \in \emptyset \)

Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 2x - 1 > 0\) là \(\emptyset \).

Qua bài giảng trên, giúp các em học sinh:

- Cách giải bất phương trình bậc hai một ẩn , bất phương trình tích , BPT chứa ẩn ở mẫu thức .

- Vận dụng định lí về dấu của tam thức bậc hai để giải BPT bậc hai , BPT tích , BPT chứa ẩn ở mẫu .

Để củng cố bài học xin mời các em cùng làm Bài kiểm tra Trắc nghiệm Toán 10 Cánh Diều Chương 3 Bài 4 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Tập nghiệm của bất phương trình: \(2{x^2}-7x-15\; \ge 0\;\) là:

  • A. \(\left( {-\infty ;-\frac{3}{2}} \right] \cup \left[ {5; + \infty } \right);\) 
  • B. \(\left[ {-\frac{3}{2};5} \right]\) 
  • C. \(\left( { - \infty ; - 5} \right] \cup \left[ {\frac{3}{2}; + \infty } \right)\) 
  • D. \(\left[ { - 5;\frac{3}{2}} \right]\)

• Câu 2:

  Tập nghiệm của bất phương trình: \(-{x^2} + 6x + 7\; \ge 0\;\) là:

  • A. \(\left( { - \infty ; - 1} \right] \cup \left[ {7; + \infty } \right)\) 
  • B. \(\left[ { - 1;7} \right]\) 
  • C. \(\left( { - \infty ; - 7} \right] \cup \left[ {1; + \infty } \right)\) 
  • D. \(\left[ { - 7;1} \right]\) 

• Câu 3:

  Giải bất phương trình \(- 2{x^2} + 3x - 7 \ge 0.\).

  • A. S=0
  • B. S={0};
  • C. S=∅;
  • D. S=R

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 10 Cánh Diều Chương 3 Bài 4 để giúp các em nắm vững bài học và các phương pháp giải bài tập.

Câu hỏi khởi động trang 49 SGK Toán 10 Cánh diều tập 1 - CD

Hoạt động 1 trang 49 SGK Toán 10 Cánh diều tập 1 - CD

Luyện tập 1 trang 49 SGK Toán 10 Cánh diều tập 1 - CD

Hoạt động 2 trang 50 SGK Toán 10 Cánh diều tập 1 - CD

Luyện tập 2 trang 50 SGK Toán 10 Cánh diều tập 1 - CD

Hoạt động 3 trang 50 SGK Toán 10 Cánh diều tập 1 - CD

Luyện tập 3 trang 51 SGK Toán 10 Cánh diều tập 1 - CD

Luyện tập 4 trang 53 SGK Toán 10 Cánh diều tập 1 - CD

Giải bài 1 trang 54 SGK Toán 10 Cánh diều tập 1 - CD

Giải bài 2 trang 54 SGK Toán 10 Cánh diều tập 1 - CD

Giải bài 3 trang 54 SGK Toán 10 Cánh diều tập 1 - CD

Giải bài 4 trang 54 SGK Toán 10 Cánh diều tập 1 - CD

Giải bài 5 trang 54 SGK Toán 10 Cánh diều tập 1 - CD

Giải bài 28 trang 56 SBT Toán 10 Cánh diều tập 1 - CD

Giải bài 29 trang 56 SBT Toán 10 Cánh diều tập 1 - CD

Giải bài 30 trang 56 SBT Toán 10 Cánh diều tập 1 - CD

Giải bài 31 trang 56 SBT Toán 10 Cánh diều tập 1 - CD

Giải bài 32 trang 57 SBT Toán 10 Cánh diều tập 1 - CD

Giải bài 33 trang 57 SBT Toán 10 Cánh diều tập 1 - CD

Giải bài 34 trang 57 SBT Toán 10 Cánh diều tập 1 - CD

Giải bài 35 trang 57 SBT Toán 10 Cánh diều tập 1 - CD

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!