Luyện tập 3 trang 51 SGK Toán 10 Cánh diều tập 1 - CD

Phương pháp giải

Bước 1: Vẽ đồ thị biểu diễn các hàm số.

Bước 2: Quan sát đồ thị và lấy các giá trị tương ứng với bất phương trình.

Hướng dẫn giải

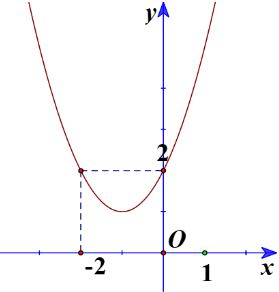
a) Ta có đồ thị:

Từ đồ thị ta thấy \({x^2} + 2x + 2 > 0\) biểu diễn phần parabol \(y = {x^2} + 2x + 2\) nằm phía trên trục hoành, tương ứng với mọi \(x \in \mathbb{R}\).

Vậy tập nghiệm của bất phương trình \({x^2} + 2x + 2 > 0\) là \(\mathbb{R}\).

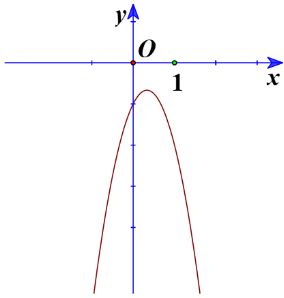
b) Ta có đồ thị:

Từ đồ thị ta thấy \( - 3{x^2} + 2x - 1 > 0\) biểu diễn phần parabol \(y =  - 3{x^2} + 2x - 1\) nằm phía trên trục hoành, tương ứng với \(x \in \emptyset \)

Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 2x - 1 > 0\) là \(\emptyset \).

-- Mod Toán 10 HỌC247