HŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 10 C├Īnh Diß╗üu ChŲ░ŲĪng 3 B├Āi 4 Bß║źt phŲ░ŲĪng tr├¼nh bß║Łc hai mß╗Öt ß║®n gi├║p c├Īc em hß╗Źc sinh nß║»m vß╗»ng phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp v├Ā ├┤n luyß╗ćn tß╗æt kiß║┐n thß╗®c.
-
C├óu hß╗Åi khß╗¤i ─æß╗Öng trang 49 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
B├Īc D┼®ng muß╗æn uß╗æn tß║źm t├┤n phß║│ng c├│ dß║Īng h├¼nh chß╗» nhß║Łt vß╗øi bß╗ü ngang 32 cm th├Ānh mß╗Öt r├Żnh dß║½n nŲ░ß╗øc bß║▒ng c├Īch chia tß║źm t├┤n ─æ├│ th├Ānh ba phß║¦n rß╗ōi gß║źp hai b├¬n lß║Īi theo mß╗Öt g├│c vu├┤ng (H├¼nh 25). ─Éß╗ā ─æß║Żm bß║Żo k─½ thuß║Łt, diß╗ćn t├Łch mß║Ęt cß║»t ngang cß╗¦a r─ünh dß║½n nŲ░ß╗øc phß║Żi lß╗øn hŲĪn hoß║Ęc bß║▒ng 120 \(cm^2\). R├Żnh dß║½n nŲ░ß╗øc phß║Żi c├│ ─æß╗Ö cao ├Łt nhß║źt l├Ā bao nhi├¬u xŪÄng-ti-m├®t?
-
Hoß║Īt ─æß╗Öng 1 trang 49 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Quan s├Īt v├Ā n├¬u ─æß║Ęc ─æiß╗ām cß╗¦a biß╗āu thß╗®c ß╗¤ vß║┐ tr├Īi cß╗¦a bß║źt phŲ░ŲĪng tr├¼nh \(3{x^2} - 4x - 8 < 0\)
-
Luyß╗ćn tß║Łp 1 trang 49 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
a) Cho hai v├Ł dß╗ź vß╗ü bß║źt phŲ░ŲĪng tr├¼nh bß║Łc hai mß╗Öt ß║®n.
b) Cho hai v├Ł dß╗ź vß╗ü bß║źt phŲ░ŲĪng tr├¼nh m├Ā kh├┤ng phß║Żi l├Ā bß║źt phŲ░ŲĪng tr├¼nh bß║Łc hai mß╗Öt ß║®n.
-
Hoß║Īt ─æß╗Öng 2 trang 50 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
a) Lß║Łp bß║Żng x├®t dß║źu cß╗¦a tam thß╗®c bß║Łc hai \(f\left( x \right) = {x^2} - x - 2\)
b) Giß║Żi bß║źt phŲ░ŲĪng tr├¼nh \({x^2} - x - 2 > 0\)
-
Luyß╗ćn tß║Łp 2 trang 50 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi c├Īc bß║źt phŲ░ŲĪng tr├¼nh bß║Łc hai sau:
a) \(3{x^2} - 2x + 4 \le 0\)
b) \( - {x^2} + 6x - 9 \ge 0\)
-
Hoß║Īt ─æß╗Öng 3 trang 50 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
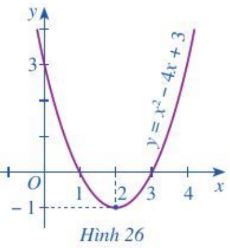
Cho bß║źt phŲ░ŲĪng tr├¼nh \({x^2} - 4x + 3 > 0\left( 2 \right)\).
Quan s├Īt parabol \(\left( P \right):{x^2} - 4x + 3\) ß╗¤ H├¼nh 26 v├Ā cho biß║┐t:
a) Bß║źt phŲ░ŲĪng tr├¼nh (2) biß╗āu diß╗ģn phß║¦n parabol (P) nß║▒m ß╗¤ ph├Ła n├Āo cß╗¦a trß╗źc ho├Ānh.
b) Phß║¦n parabol (P) nß║▒m ph├Ła tr├¬n trß╗źc ho├Ānh ß╗®ng vß╗øi nhß╗»ng gi├Ī trß╗ŗ n├Āo cß╗¦a x.
-
Luyß╗ćn tß║Łp 3 trang 51 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi mß╗Śi bß║źt phŲ░ŲĪng tr├¼nh bß║Łc hai sau bß║▒ng c├Īch sß╗Ł dß╗źng ─æß╗ō thß╗ŗ:
a) \({x^2} + 2x + 2 > 0\)
b) \( - 3{x^2} + 2x - 1 > 0\)
-
Luyß╗ćn tß║Łp 4 trang 53 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Tß╗Ģng chi ph├Ł T (─æŲĪn vß╗ŗ t├Łnh: ngh├¼n ─æß╗ōng) ─æß╗ā sß║Żn xuß║źt Q sß║Żn phß║®m ─æŲ░ß╗Żc cho bß╗¤i biß╗āu thß╗®c \(T = {Q^2} + 30Q + 3300\); gi├Ī b├Īn cß╗¦a 1 sß║Żn phß║®m l├Ā 170 ngh├¼n ─æß╗ōng. Sß╗æ sß║Żn phß║®m ─æŲ░ß╗Żc sß║Żn xuß║źt trong khoß║Żng n├Āo ─æß╗ā ─æß║Żm bß║Żo kh├┤ng bß╗ŗ lß╗Ś (giß║Ż thiß║┐t c├Īc sß║Żn phß║®m ─æŲ░ß╗Żc b├Īn hß║┐t)?
-
Giß║Żi b├Āi 1 trang 54 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Trong c├Īc bß║źt phŲ░ŲĪng tr├¼nh sau, bß║źt phŲ░ŲĪng tr├¼nh n├Āo l├Ā bß║źt phŲ░ŲĪng tr├¼nh bß║Łc hai mß╗Öt ß║®n? V├¼ sao?
a) \( - 2x + 2 < 0\)
b) \(\frac{1}{2}{y^2} - \sqrt 2 \left( {y + 1} \right) \le 0\)
c) \({y^2} + {x^2} - 2x \ge 0\)
-
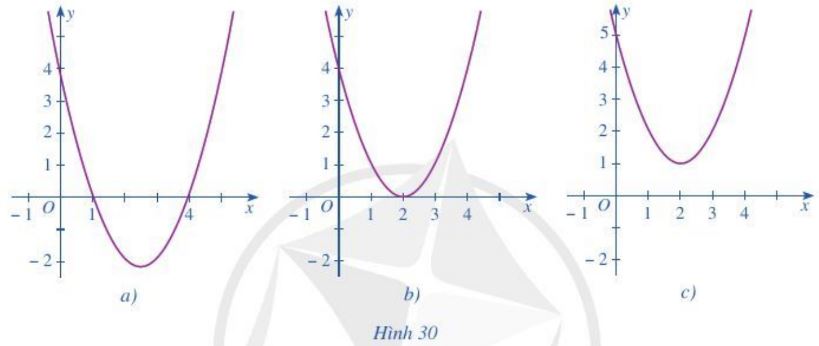
Giß║Żi b├Āi 2 trang 54 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Dß╗▒a v├Āo ─æß╗ō thß╗ŗ h├Ām sß╗æ bß║Łc hai \(y = f\left( x \right)\) trong mß╗Śi H├¼nh 30a, 30b, 30c, h├Ży viß║┐t tß║Łp nghiß╗ćm cß╗¦a mß╗Śi bß║źt phŲ░ŲĪng tr├¼nh sau: \(f\left( x \right) > 0;f\left( x \right) < 0;\)\(f\left( x \right) \ge 0;f\left( x \right) \le 0\).
-
Giß║Żi b├Āi 3 trang 54 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi c├Īc bß║źt phŲ░ŲĪng tr├¼nh bß║Łc hai sau:
a) \(2{x^2} - 5x + 3 > 0\)
b) \( - {x^2} - 2x + 8 \le 0\)
c) \(4{x^2} - 12x + 9 < 0\)
d) \( - 3{x^2} + 7x - 4 \ge 0\)
-
Giß║Żi b├Āi 4 trang 54 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
T├¼m m ─æß╗ā phŲ░ŲĪng tr├¼nh \(2{x^2} + \left( {m + 1} \right)x + m - 8 = 0\) c├│ nghiß╗ćm.
-
Giß║Żi b├Āi 5 trang 54 SGK To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
X├®t hß╗ć toß║Ī ─æß╗Ö Oth tr├¬n mß║Ęt phß║│ng, trong ─æ├│ trß╗źc Ot biß╗āu thß╗ŗ thß╗Øi gian t (t├Łnh bß║▒ng gi├óy) v├Ā trß╗źc Oh biß╗āu thß╗ŗ ─æß╗Ö cao h (t├Łnh bß║▒ng m├®t). Mß╗Öt quß║Ż b├│ng ─æŲ░ß╗Żc ─æ├Ī l├¬n tß╗½ ─æiß╗ām A(0; 0,2) v├Ā chuyß╗ān ─æß╗Öng theo quß╗╣ ─æß║Īo l├Ā mß╗Öt cung parabol. Quß║Ż b├│ng ─æß║Īt ─æß╗Ö cao 8,5 m sau 1 gi├óy v├Ā ─æß║Īt ─æß╗Ö cao 6 m sau 2 gi├óy.
a) H├Ży t├¼m h├Ām sß╗æ bß║Łc hai biß╗āu thß╗ŗ quß╗╣ ─æß║Īo chuyß╗ān ─æß╗Öng cß╗¦a quß║Ż b├│ng.
b) Trong khoß║Żng thß╗Øi gian n├Āo th├¼ quß║Ż b├│ng vß║½n chŲ░a chß║Īm ─æß║źt?
-
Giß║Żi b├Āi 28 trang 56 SBT To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Trong c├Īc bß║źt phŲ░ŲĪng tr├¼nh sau, bß║źt phŲ░ŲĪng tr├¼nh n├Āo kh├┤ng l├Ā bß║źt phŲ░ŲĪng tr├¼nh bß║Łc hai mß╗Öt ß║®n?
A. \( - 2{x^2} + 3x < 0\)
B. \(0,5{y^2} - \sqrt 3 \left( {y - 2} \right) \le 0\)
C. \({x^2} - 2xy - 3 \ge 0\)
D. \(\sqrt 2 {x^2} - 3 \ge 0\)
-
Giß║Żi b├Āi 29 trang 56 SBT To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Tß║Łp nghiß╗ćm cß╗¦a bß║źt phŲ░ŲĪng tr├¼nh \( - {x^2} + 3x + 18 \ge 0\) l├Ā:
A. \(\left[ { - 3;6} \right]\)
B. \(\left( { - 3;6} \right)\)
C. \(x \in \left( { - \infty ; - 3} \right) \cup \left( {6; + \infty } \right)\)
D. \(x \in \left( { - \infty ; - 3} \right] \cup \left[ {6; + \infty } \right)\)
-
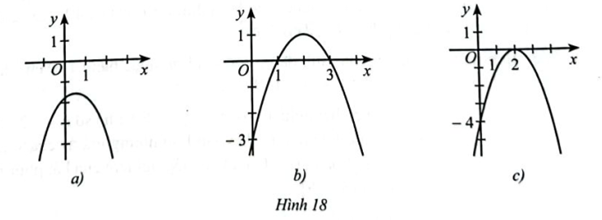
Giß║Żi b├Āi 30 trang 56 SBT To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Dß╗▒a v├Āo ─æß╗ō thß╗ŗ h├Ām sß╗æ bß║Łc hai \(y = f\left( x \right)\) trong mß╗Śi H├¼nh 18a, 18b, 18c, h├Ży viß║┐t tß║Łp nghiß╗ćm c├Īc bß║źt phŲ░ŲĪng tr├¼nh sau: \(f\left( x \right) > 0;f\left( x \right) < 0;f\left( x \right) \ge 0;f\left( x \right) \le 0\)
-
Giß║Żi b├Āi 31 trang 56 SBT To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Giß║Żi c├Īc bß║źt phŲ░ŲĪng tr├¼nh bß║Łc hai sau:
a) \(3{x^2} - 8x + 5 > 0\)
b) \( - 2{x^2} - x + 3 \le 0\)
c) \(25{x^2} - 10x + 1 < 0\)
d) \( - 4{x^2} + 5x + 9 \ge 0\)
-
Giß║Żi b├Āi 32 trang 57 SBT To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
T├¼m giao c├Īc tß║Łp nghiß╗ćm cß╗¦a hai bß║źt phŲ░ŲĪng tr├¼nh \( - 3{x^2} + 7x + 10 \ge 0\) v├Ā \( - 2{x^2} - 9x + 11 > 0\)
-
Giß║Żi b├Āi 33 trang 57 SBT To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
T├¼m \(m\) ─æß╗ā phŲ░ŲĪng tr├¼nh \( - {x^2} + \left( {m + 2} \right)x + 2m - 10 = 0\) c├│ nghiß╗ćm
-
Giß║Żi b├Āi 34 trang 57 SBT To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
X├®t hß╗ć tß╗Źa ─æß╗Ö \(Oth\) trong mß║Ęt phß║│ng, trong ─æ├│ trß╗źc \(Ot\) biß╗āu thß╗ŗ thß╗Øi gian \(t\) (t├Łnh bß║▒ng gi├óy) v├Ā trß╗źc \(Oh\) biß╗āu thß╗ŗ ─æß╗Ö cao \(h\) (t├Łnh bß║▒ng m├®t). Mß╗Öt quß║Ż b├│ng ─æŲ░ß╗Żc ─æ├Ī l├¬n tß╗½ ─æiß╗ām \(A\left( {0;0,3} \right)\) v├Ā chuyß╗ān ─æß╗Öng theo quß╗╣ ─æß║Īo l├Ā mß╗Öt cung parabol. Quß║Ż b├│ng ─æß║Īt ─æß╗Ö cao 8m sau 1 gi├óy, v├Ā ─æß║Īt ─æß╗Ö cao 6m sau 2 gi├óy. Trong khoß║Żng thß╗Øi gian n├Āo (t├Łnh bß║▒ng gi├óy) th├¼ quß║Ż b├│ng ß╗¤ ─æß╗Ö cao lŲĪn hŲĪn 5m v├Ā nhß╗Å hŲĪn 7m (l├Ām tr├▓n kß║┐t quß║Ż ─æß║┐n h├Āng phß║¦n ngh├¼n)?
-
Giß║Żi b├Āi 35 trang 57 SBT To├Īn 10 C├Īnh diß╗üu tß║Łp 1 - CD
Mß╗Öt t├¼nh huß╗æng trong huß║źn luyß╗ćn ph├Īo binh ─æŲ░ß╗Żc m├┤ tß║Ż nhŲ░ sau: Trong mß║Ęt phß║│ng tß╗Źa ─æß╗Ö \(Oxy\) (─æŲĪn vß╗ŗ tr├¬n hai trß╗źc t├Łnh theo m├®t), mß╗Öt vi├¬n ─æß║Īn ─æŲ░ß╗Żc bß║»n tß╗½ vß╗ŗ tr├Ł \(O\left( {0;0} \right)\) theo quß╗╣ ─æß║Īo l├Ā ─æŲ░ß╗Øng parabol \(y = - \frac{9}{{1\;000\;000}}{x^2} + \frac{3}{{100}}x\). T├¼m khoß║Żng c├Īch theo trß╗źc ho├Ānh cß╗¦a vi├¬n ─æß║Īn so vß╗øi vß╗ŗ tr├Ł bß║»n khi vi├¬n ─æß║Īn ─æang ß╗¤ ─æß╗Ö cao lß╗øn hŲĪn 15m (l├Ām tr├▓n kß║┐t quß║Ż ─æß║┐n h├Āng phß║¦n tr─ām theo ─æŲĪn vß╗ŗ m├®t).

.JPG)