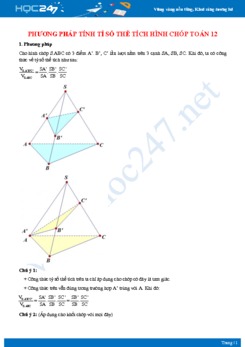
Các em học sinh có thể tham khảo nội dung tài liệu Lý thuyết và bài tập về tính thể tích hình chóp Toán 12 được HOC247 sưu tầm và tổng hợp bên dưới đây. Tài liệu gồm phần tóm tắt lý thuyết và các câu hỏi trắc nghiệm có đáp án cụ thể hi vọng sẽ giúp các em ôn luyện và củng cố kiến thức chuẩn bị thật tốt cho kì thi sắp đến.
I. LÝ THUYẾT
1) Nếu khối chóp đã cho có chiều cao h và diện tích đáy B thì thể tích tính theo công thức V = \(\frac13\)Bh
.png?enablejsapi=1)
2) Nếu khối chóp cần tính thể tích chưa biết chiều cao thì ta phải xác định được vị trí chân đường cao trên đáy.
a) Chóp có cạnh bên vuông góc chiều cao chính là cạnh bên.
b) Chóp có hai mặt bên vuông góc đáy đường cao là giao tuyến của hai mặt bên vuông góc đáy.
c) Chóp có mặt bên vuông góc đáy chiều cao của mặt bên vuông góc đáy.
d) Chóp đều chiều cao hạ từ đỉnh đến tâm đa giác đáy.
e) Chóp có hình chiếu vuông góc của một đỉnhlên xuống mặt đáy thuộc cạnh mặt đáy đường cao là từ đỉnh tới hình chiếu.
Chú ý: Các công thức tính diện tích đáy
a) Tam giác:
S = \(\frac12\).a.ha = \(\frac12\)b.hb = \(\frac12\)c.hc
S = \(\frac12\)bc.sinA = \(\frac12\)ca.sinB = \(\frac12\)ab.sinA
S = pr
S = \(\frac{abc}{4R}\)
S = \(\sqrt{p(p-a)(p-b)(p-c)}\)
Tam giác ABC vuông tại A: 2S = AB.AC = BC.AH
Tam giác ABC đều, cạnh a: S = \(\frac{a^2.\sqrt3}{4}\)
b) Hình vuông cạnh a: S = a2 (a: cạnh hình vuông)
c) Hình chữ nhật: S = a.b (a, b: hai kích thước)
d) Hình bình hành ABCD: S = đáy \(\times\) cao = AB.AD.sinBAD
e) Hình thoi ABCD: S = AB.AD.sinBAD = \(\frac12\)AC.BD
f) Hình thang: S = \(\frac12\)(a+b).h (a, b: hai đáy, h: chiều cao)
g) Tứ giác ABCD có hai đường chéo vuông góc: S = \(\frac12\) AC.BD
II. BÀI TẬP
Câu 1: Thể tích (cm3) khối tứ diện đều cạnh bằng \(\frac{2}{3}\)cm là :
A. \(\frac{2}{3}\)
B. \(\frac{2\sqrt{2}}{81}\)
C. \(\frac{2\sqrt{3}}{81}\)
D. \(\frac{\sqrt{3}}{18}\)
Hướng dẫn giải:
Gọi cạnh tứ diện đều là a. Dễ dàng tính được
V = a3. \(\frac{\sqrt{2}}{12}\).
Thay a = \(\frac{2}{3}\) ta được V = \(\frac{2\sqrt{2}}{81}\)
Chọn đáp án B.
Câu 2: Thể tích của khối bát diện đều cạnh a là:
A. \({{a}^{3}}\frac{\sqrt{2}}{3}\)
B. \({{a}^{3}}\frac{\sqrt{2}}{6}\)
C. \({{a}^{3}}\frac{\sqrt{3}}{2}\)
D. \({{a}^{3}}\sqrt{6}\)
Hướng dẫn giải:
Thề tích của khối chóp tứ giác đều có các cạnh bằng a có thể tích là V1=\(\frac{{{a}^{3}}\sqrt{2}}{6}\)
Mà thể tích của khối bát diện đều bằng 2V1.
Do đó thể tích khối bát diện đều là V=\({{a}^{3}}\frac{\sqrt{2}}{3}\).
Chọn đáp án A.
Câu 3: Kim tự tháp Kê-ốp ở Ai Cập được xây dựng vào khoảng 2500 năm trước Công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao 147m, cạnh đáy dài 230m. Thế tích \(V\) của khối chóp đó là?
A. \(V=2592100\)m3
B. \(V=7776300\)m3
C. \(V=2592300\)m3
D. \(V=3888150\)m3
Hướng dẫn giải:
+ Thể tích của kim tự tháp Kê - ốp là \(V=\frac{1}{3}{{.147.230}^{2}}=2592100\,{{m}^{3}}\)
Chọn đáp án A.
Câu 4: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, tất cả các cạnh bên tạo với mặt phẳng đáy một góc 600. Thể tích của khối chóp S.ABCD là:
A. \(\frac{{{a}^{3}}\sqrt{6}}{3}\)
B. \(\frac{{{a}^{3}}\sqrt{3}}{2}\)
C. \(\frac{{{a}^{3}}}{3}\)
D. \(\frac{{{a}^{3}}\sqrt[{}]{3}}{6}\)
Hướng dẫn giải:
.png)
Gọi H là giao điểm của AC và \(BD.\) Do S.ABCD là chóp đều nên SO\(\bot \) (ABCD)
Theo giả thiết ta có \(\widehat{SAO}=\widehat{SBO}=\widehat{SCO}\widehat{=SDO}={{60}^{0}}\)
Trong tam giác OBS ta có \(SO=OB.tan{{60}^{0}}=\frac{a\sqrt{2}}{2}.\sqrt{3}=\frac{a\sqrt{6}}{2}\)
Thể tích khối chóp \(V=\frac{1}{3}{{S}_{ABCD}}.SO=\frac{1}{3}{{a}^{2}}.\frac{a\sqrt{6}}{2}=\frac{1}{3}{{a}^{3}}\sqrt{6}\)
Chọn đáp án B.
Câu 5: Một khối chóp tam giác đều có cạnh bên bằng b, chiều cao h. Khi đó thể tích khối chóp là:
A. \(\frac{\sqrt{3}}{4}({{b}^{2}}-{{h}^{2}})b\)
B. \(\frac{\sqrt{3}}{4}({{b}^{2}}-{{h}^{2}})h\)
C. \(\frac{\sqrt{3}}{8}({{b}^{2}}-{{h}^{2}})h\)
D. \(\frac{\sqrt{3}}{12}({{b}^{2}}-{{h}^{2}})\)
Hướng dẫn giải:
.png)
Gọi M là trung điểm BC của hinh chóp S.ABC và H là hình chiếu của S trên mặt phẳng (ABC).
Khi đó AH=\(\sqrt{{{b}^{2}}-{{h}^{2}}}\), AM= \(\frac{3}{2}\sqrt{{{b}^{2}}-{{h}^{2}}}\).
Gọi x là cạnh của tam giác đều ABC suy ra
\(AM=\frac{x\sqrt{3}}{2}\Rightarrow \frac{3\sqrt{{{b}^{2}}-{{h}^{2}}}}{2}=\frac{x\sqrt{3}}{2}\Rightarrow {{x}^{2}}=3({{b}^{2}}-{{h}^{2}})\)
Diện tích tam giác ABC: \(S=\frac{3\sqrt{3}\left( {{b}^{2}}-{{h}^{2}} \right)}{4}\Rightarrow {{V}_{SABC}}=\frac{\sqrt{3}}{4}({{b}^{2}}-{{h}^{2}})h\)
Chọn đáp án B.
Câu 6: Tính thể tích của khối chóp S.ABCD có tất cả các cạnh bằng 1.
A. \(\frac{\sqrt{3}}{2}\)
B. \(\frac{\sqrt{3}}{6}\)
C. \(\frac{\sqrt{2}}{6}\)
D. \(\frac{\sqrt{2}}{2}\)
Hướng dẫn giải:
Gọi O là tâm của ABCD, ta có \(V=\frac{1}{3}.SO.{{S}_{ABCD}}=\frac{1}{3}\sqrt{\frac{1}{2}}.1=\frac{\sqrt{2}}{6}\)
Chọn đáp án C.
Câu 7: Cho hình chóp tam giác đều có cạnh đáy bằng a và cạnh bên tạo với đáy một góc \({{60}^{0}}\). Thể tích của khối chóp đó bằng:
A. \(\frac{{{a}^{3}}\sqrt{3}}{12}\)
B. \(\frac{{{a}^{3}}\sqrt{3}}{6}\)
C. \(\frac{{{a}^{3}}\sqrt{3}}{36}\)
D. \(\frac{{{a}^{3}}\sqrt{3}}{18}\)
Hướng dẫn giải:
\(V=\frac{{{a}^{3}}\tan \varphi }{12}=\frac{{{a}^{3}}\sqrt{3}}{12}\) nên
Chọn đáp án A.
Câu 8: Cho hình chóp tam giác đều S.ABCD, cạnh đáy bằng a. Mặt bên tạo với mặt đáy một góc 600. Tính thể tích V của hình chóp S.ABC.
A. \(V=\frac{{{a}^{3}}\sqrt{3}}{2}\)
B. \(V=\frac{{{a}^{3}}\sqrt{3}}{6}\)
C. \(V=\frac{{{a}^{3}}\sqrt{3}}{12}\)
D. \(V=\frac{{{a}^{3}}\sqrt{3}}{24}\)
Hướng dẫn giải:
.png)
Gọi các điểm như hình vẽ. Theo đề suy ra \(\widehat{SIA}={{60}^{0}}\)
Ta có \(AI=\frac{a\sqrt{3}}{2}\Rightarrow HI=\frac{a\sqrt{3}}{6}\Rightarrow SH=\frac{a}{2}\)
Vậy \(V=\frac{{{a}^{3}}\sqrt{3}}{24}\)
Chọn đáp án D.
Câu 9: Cho hình chóp tứ giác đều \(S.ABCD\) có \(AB=a\), SA=a\(\sqrt{2}\). Gọi M, N, P lần lượt là trung điểm của các cạnh SA, SB và CD. Tính thể tích \(V\) của tứ diện AMNP.
A. \(V=\frac{{{a}^{3}}\sqrt{6}}{36}\)
B. \(V=\frac{{{a}^{3}}\sqrt{6}}{48}\)
C. \(V=\frac{{{a}^{3}}\sqrt{3}}{48}\).
D. \(V=\frac{{{a}^{3}}\sqrt{6}}{12}\)
Hướng dẫn giải:
Gọi O là tâm của đáy ABCD. Tính được SO=\(\frac{a\sqrt{6}}{2}\)
VAMNP=\(\frac{1}{4}\)VABSP=\(\frac{1}{8}\)VABCD=\(\frac{1}{8}.\frac{1}{3}SO.A{{B}^{2}}\) =\( \frac{{{a}^{3}}\sqrt{6}}{48}\)
Chọn đáp án B.
Câu 10: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng \(2a\), góc giữa mặt bên và mặt đáy bằng 600. Tính theo a thể tích khối chóp S.ABCD
A. \(\frac{4{{a}^{3}}\sqrt{3}}{3}\)
B. \(\frac{{{a}^{3}}\sqrt{3}}{3}\)
C. \(\frac{2{{a}^{3}}\sqrt{3}}{3}\)
D. \(\frac{2{{a}^{3}}\sqrt{6}}{3}\)
Hướng dẫn giải:
.png)
Gọi O là tâm hình vuông ABCD, M là trung điểm CD.
Khi đó SO là đường cao hình chóp, góc SMO là góc giữa mặt bên và mặt đáy của hình chóp.
\(OM=\frac{AD}{2}=\frac{2a}{2}=a\Rightarrow SO=OM.\tan {{60}^{0}}=a\sqrt{3}\).
Suy ra \({{V}_{S.ABCD}}=\frac{1}{3}{{S}_{ABCD}}.SO=\frac{1}{3}{{\left( 2a \right)}^{2}}.a\sqrt{3}=\frac{4{{a}^{3}}\sqrt{3}}{3}\)
Chọn đáp án A.
...
--(Nội dung đầy đủ, chi tiết vui lòng xem tại online hoặc đăng nhập để tải về máy)--
Trên đây là một phần trích đoạn nội dung Lý thuyết và bài tập về tính thể tích hình chóp Toán 12. Để xem thêm nhiều tài liệu tham khảo hữu ích khác các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.
Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.
Các em quan tâm có thể tham khảo thêm các tài liệu cùng chuyên mục:
Chúc các em học tốt!
Tài liệu liên quan
Tư liệu nổi bật tuần
- Xem thêm