HOC247 giß╗øi thiß╗ću vß╗øi c├Īc em t├Āi liß╗ću Tß╗Ģng hß╗Żp c├┤ng thß╗®c v├Ā b├Āi tß║Łp t├Łnh thß╗ā t├Łch c├Īc dß║Īng khß╗æi l─āng trß╗ź hay nhß║źt lß╗øp 12 c├│ lß╗Øi giß║Żi chi tiß║┐t, ─æŲ░ß╗Żc HOC247 bi├¬n tß║Łp v├Ā tß╗Ģng hß╗Żp gi├║p c├Īc em ├┤n tß║Łp v├Ā r├©n luyß╗ćn. Hi vß╗Źng t├Āi liß╗ću n├Āy sß║Į c├│ ├Łch cho c├Īc em, ch├║c c├Īc em c├│ kß║┐t quß║Ż hß╗Źc tß║Łp thß║Łt tß╗æt.
I. THß╗é T├ŹCH KHß╗ÉI L─éNG TRß╗ż
|
Ch├║ ├Į:
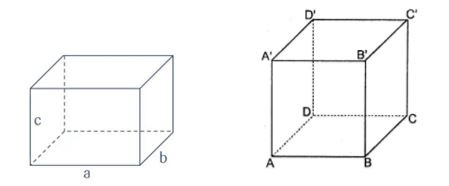
1. Th├¬╠ē ti╠üch kh├┤╠üi hi╠Ćnh h├┤╠Żp chŲ░╠ā nh├ó╠Żt: V=abc ŌćÆ Th├¬╠ē ti╠üch kh├┤╠üi l├ó╠Żp phŲ░ŲĪng: \({V = {a^3}}\)
H├¼nh hß╗Öp chß╗» nhß║Łt H├¼nh lß║Łp phŲ░ŲĪng
2. H├¼nh l─āng trß╗ź ─æß╗üu l├Ā h├¼nh l─āng trß╗ź ─æß╗®ng c├│ ─æ├Īy l├Ā ─æa gi├Īc ─æß╗üu
+ H├¼nh l─āng trß╗ź tam gi├Īc ─æß╗üu l├Ā h├¼nh l─āng trß╗ź ─æß╗®ng c├│ ─æ├Īy l├Ā tam gi├Īc ─æß╗üu.
+ H├¼nh l─āng trß╗ź tß╗® gi├Īc ─æß╗üu l├Ā h├¼nh l─āng trß╗ź ─æß╗®ng c├│ ─æ├Īy l├Ā h├¼nh vu├┤ng.
II. C├üC C├öNG THß╗©C T├ŹNH NHANH Tß╗ł Lß╗å THß╗é T├ŹCH Cß╗”A KHß╗ÉI L─éNG TRß╗ż
1. Khß╗æi trß╗ź tam gi├Īc
- Ba╠Ći toa╠ün 1: Gß╗Źi V l├Ā thß╗ā t├Łch khß╗æi l─āng trß╗ź, l├Ā thß╗ā t├Łch khß╗æi ch├│p tß║Īo th├Ānh tß╗½ 4 trong 6 ─æß╗ēnh cß╗¦a l─āng trß╗ź. Khi ─æ├│: \(\frac{{{V_4}}}{V} = \frac{1}{3}\) .
Cho h├¼nh l─āng trß╗ź tam gi├Īc. Khi ─æ├│: \(\frac{{{V_{C.A'B'C'}}}}{{{V_{ABC.A'B'C'}}}} = \frac{1}{3}\).
- Ba╠Ći toa╠ün 2: Gß╗Źi \(V\) l├Ā thß╗ā t├Łch khß╗æi l─āng trß╗ź, \({{V}_{5}}\) l├Ā thß╗ā t├Łch khß╗æi ch├│p tß║Īo th├Ānh tß╗½ 5 trong 6 ─æß╗ēnh cß╗¦a l─āng trß╗ź. Khi ─æ├│: \(\frac{{{V}_{5}}}{V}=\frac{2}{3}\).
Cho h├¼nh l─āng trß╗ź tam gi├Īc \(ABC.A'B'C'\). Khi ─æ├│: \(\frac{{{V}_{A'B'ABC}}}{{{V}_{ABC.A'B'C'}}}=\frac{2}{3}\).
- Ba╠Ći toa╠ün 3: Cho h├¼nh l─āng trß╗ź tam gi├Īc \(ABC.A'B'C'\). Mß║Ęt phß║│ng cß║»t c├Īc ─æŲ░ß╗Øng thß║│ng \(AA',BB',CC'\) lß║¦n lŲ░ß╗Żt tß║Īi \(M,N,P\) sao cho \(\frac{AM}{AA'}=a,\frac{BN}{BB'}=b,\frac{CP}{CC'}=c\) th├¼ \(\frac{{{V}_{ABC.MNP}}}{{{V}_{ABC.A'B'C'}}}=\frac{a+b+c}{3}\)
2. Khối hộp
- Ba╠Ći toa╠ün 1: Gß╗Źi \(V\) l├Ā thß╗ā t├Łch khß╗æi hß╗Öp, \({{V}_{4}}\) l├Ā thß╗ā t├Łch khß╗æi ch├│p tß║Īo th├Ānh tß╗½ 4 trong 8 ─æß╗ēnh cß╗¦a khß╗æi hß╗Öp v├Ā 4 ─æß╗ēnh n├Āy thuß╗Öc hai ─æŲ░ß╗Øng ch├®o cß╗¦a hai mß║Ęt song song . Khi ─æ├│: \(\frac{{{V}_{4}}}{V}=\frac{1}{3}\).
- Ba╠Ći toa╠ün 2: Gß╗Źi \(V\) l├Ā thß╗ā t├Łch khß╗æi hß╗Öp, \({{V}_{4}}\) l├Ā thß╗ā t├Łch khß╗æi ch├│p tß║Īo th├Ānh tß╗½ 4 trong 8 ─æß╗ēnh cß╗¦a khß╗æi hß╗Öp ( trß╗½ trŲ░ß╗Øng hß╗Żp 4 ─æß╗ēnh n├Āy thuß╗Öc hai ─æŲ░ß╗Øng ch├®o cß╗¦a hai mß║Ęt song song) . Khi ─æ├│: \(\frac{{{V}_{4}}}{V}=\frac{1}{6}\).
- Ba╠Ći toa╠ün 3: Gß╗Źi \(V\) l├Ā thß╗ā t├Łch khß╗æi hß╗Öp, \({{V}_{5}}\) l├Ā thß╗ā t├Łch khß╗æi ch├│p tß║Īo th├Ānh tß╗½ 5 trong 8 ─æß╗ēnh cß╗¦a khß╗æi hß╗Öp (1 ─æß╗ēnh thuß╗Öc mß║Ęt phß║│ng ─æ├Īy, 4 ─æß╗ēnh c├▓n lß║Īi thuß╗Öc mß║Ęt phß║│ng ─æ├Īy c├▓n lß║Īi). Khi ─æ├│: \(\frac{{{V}_{5}}}{V}=\frac{1}{3}\).
- Ba╠Ći toa╠ün 4: Cho h├¼nh hß╗Öp \(ABCD.A'B'C'D'\). Mß║Ęt phß║│ng cß║»t c├Īc ─æŲ░ß╗Øng thß║│ng \(AA',BB',CC',DD'\) lß║¦n lŲ░ß╗Żt tß║Īi \(M,Q,P,N\) sao cho \(\frac{AM}{AA'}=a,\frac{BQ}{BB'}=b,\frac{CP}{CC'}=c,\frac{DN}{DD'}=d\) v├Ā \(a+c=b+d\) th├¼:
\[\frac{{{V}_{ABCD.MQPN}}}{{{V}_{ABCD.A'B'C'D'}}}=\frac{a+b+c+d}{4}=\frac{a+c}{2}=\frac{b+d}{2}\]
Ch├║ ├Į: Hai khß╗æi ─æa diß╗ćn ─æß╗ōng dß║Īng vß╗øi tß╗ē sß╗æ th├¼ tß╗ē lß╗ć thß╗ā t├Łch cß╗¦a ch├║ng l├Ā hay
III. TRß║«C NGHIß╗åM (L├Ø THUYß║ŠT V├Ć Vß║¼N Dß╗żNG)
C├óu 1.(─Éß╗ü thi THPT Quß╗æc Gia ŌĆō N─ām 2022 ŌĆōM├Ż ─æß╗ü 101, 102)
Cho khß╗æi l─āng trß╗ź c├│ diß╗ćn t├Łch ─æ├Īy \(3{{a}^{2}}\) v├Ā chiß╗üu cao \(2a\). Thß╗ā t├Łch khß╗æi l─āng trß╗ź ─æ├Ż cho bß║▒ng:
A. \({{a}^{3}}\). B. \(6{{a}^{3}}\). C. \(3{{a}^{3}}\). D. \(2{{a}^{3}}\).
Lß╗Øi giß║Żi
Chß╗Źn B.
Thß╗ā t├Łch khß╗æi l─āng trß╗ź: \(V=B.h=3{{a}^{2}}.2a=6{{a}^{3}}\).
C├óu 2.(─Éß╗ü thi THPT Quß╗æc Gia ŌĆō N─ām 2022 ŌĆōM├Ż ─æß╗ü 103, 104)
Cho khß╗æi ch├│p v├Ā khß╗æi l─āng trß╗ź c├│ diß╗ćn t├Łch ─æ├Īy, chiß╗üu cao tŲ░ŲĪng ß╗®ng bß║▒ng nhau v├Ā c├│ thß╗ā t├Łch lß║¦n lŲ░ß╗Żt l├Ā \({{V}_{1}},{{V}_{2}}\). Tß╗ē sß╗æ \(\frac{{{V}_{1}}}{{{V}_{2}}}\) bß║▒ng
A. \(\frac{2}{3}\). B. 3. C. \(\frac{3}{2}\). D. \(\frac{1}{3}\).
Lß╗Øi giß║Żi
Chß╗Źn D.
Gß╗Źi diß╗ćn t├Łch ─æ├Īy v├Ā chiß╗üu cao tŲ░ŲĪng ß╗®ng cß╗¦a khß╗æi ch├│p v├Ā khß╗æi l─āng trß╗ź l├Ā B v├Ā h
Ta c├│ \(\left\{ \begin{array}{l} {V_1} = \frac{1}{3}Bh\\ {V_2} = Bh \end{array} \right. \Rightarrow \frac{{{V_1}}}{{{V_2}}} = \frac{1}{3}\)
C├óu 3.Thß╗ā t├Łch khß╗æi l─āng trß╗ź c├│ diß╗ćn t├Łch ─æ├Īy \(B\) v├Ā c├│ chiß╗üu cao \(h\) l├Ā
A. \(V=B.h\). B. \(V=\frac{4}{3}Bh\). C. \(V=\frac{1}{3}Bh\). D. \(V=3Bh\).
Lß╗Øi giß║Żi
Chß╗Źn A
Thß╗ā t├Łch khß╗æi l─āng trß╗ź c├│ diß╗ćn t├Łch ─æ├Īy \(B\) v├Ā c├│ chiß╗üu cao \(h\) l├Ā: \(V=B.h\).
C├óu 4. Chiß╗üu cao cß╗¦a khß╗æi l─āng trß╗ź c├│ diß╗ćn t├Łch ─æ├Īy \(B\) v├Ā thß╗ā t├Łch \(V\) l├Ā
A. \(h=\frac{3V}{B}\). B. \(h=\frac{V}{3B}\). C. \(h=\frac{B}{V}\). D. \(h=\frac{V}{B}\).
Lß╗Øi giß║Żi
Chß╗Źn D
Chiß╗üu cao cß╗¦a khß╗æi l─āng trß╗ź c├│ diß╗ćn t├Łch ─æ├Īy \(B\) v├Ā thß╗ā t├Łch \(V\) l├Ā: \(h=\frac{V}{B}\).
C├óu 5. Diß╗ćn t├Łch ─æ├Īy cß╗¦a khß╗æi l─āng trß╗ź c├│ thß╗ā t├Łch \(V\) v├Ā c├│ chiß╗üu cao \(h\) l├Ā
A. \(B=\frac{3V}{h}\). B. \(B=\frac{3h}{V}\). C. \(B=\frac{V}{h}\). D. \(B=\frac{h}{V}\).
Lß╗Øi giß║Żi
Chß╗Źn C
Diß╗ćn t├Łch ─æ├Īy cß╗¦a khß╗æi l─āng trß╗ź c├│ thß╗ā t├Łch \(V\) v├Ā c├│ chiß╗üu cao \(h\) l├Ā: \(B=\frac{V}{h}\).
---(─Éß╗ā xem ─æß║¦y ─æß╗¦ nß╗Öi dung ─æß╗ü thi v├Ā ─æ├Īp ├Īn chi tiß║┐t, c├Īc em vui l├▓ng xem online hoß║Ęc ─æ─āng nhß║Łp ─æß╗ā tß║Żi vß╗ü m├Īy)---
Tr├¬n ─æ├óy l├Ā mß╗Öt phß║¦n tr├Łch ─æoß║Īn nß╗Öi dung Tß╗Ģng hß╗Żp c├┤ng thß╗®c v├Ā b├Āi tß║Łp t├Łnh thß╗ā t├Łch c├Īc dß║Īng khß╗æi l─āng trß╗ź hay nhß║źt. ─Éß╗ā xem th├¬m nhiß╗üu t├Āi liß╗ću tham khß║Żo hß╗»u ├Łch kh├Īc c├Īc em chß╗Źn chß╗®c n─āng xem online hoß║Ęc ─æ─āng nhß║Łp v├Āo trang hoc247.net ─æß╗ā tß║Żi t├Āi liß╗ću vß╗ü m├Īy t├Łnh.
Hy vß╗Źng t├Āi liß╗ću n├Āy sß║Į gi├║p c├Īc em hß╗Źc sinh ├┤n tß║Łp tß╗æt v├Ā ─æß║Īt th├Ānh t├Łch cao trong hß╗Źc tß║Łp.
C├Īc em quan t├óm c├│ thß╗ā tham khß║Żo th├¬m c├Īc t├Āi liß╗ću c├╣ng chuy├¬n mß╗źc:
-
Chuy├¬n ─æß╗ü tß╗ē lß╗ć thß╗ā t├Łch cß╗¦a c├Īc khß╗æi ─æa diß╗ćn To├Īn 12
-
Chuy├¬n ─æß╗ü bß║źt phŲ░ŲĪng tr├¼nh m┼® v├Ā l├┤ragit vß║Łn dß╗źng cao ├┤n thi tß╗æt nghiß╗ćp THPT
Ch├║c c├Īc em hß╗Źc tß║Łp tß╗æt!
T├Āi liß╗ću li├¬n quan
TŲ░ liß╗ću nß╗Ģi bß║Łt tuß║¦n
- Xem thêm