Công thức tính tỉ số lượng giác của góc nhọn và bài tập áp dụng Toán 9 chi tiết nhất

       1. Các tỉ số lượng giác của góc nhọn  (hình) được định nghĩa như sau:

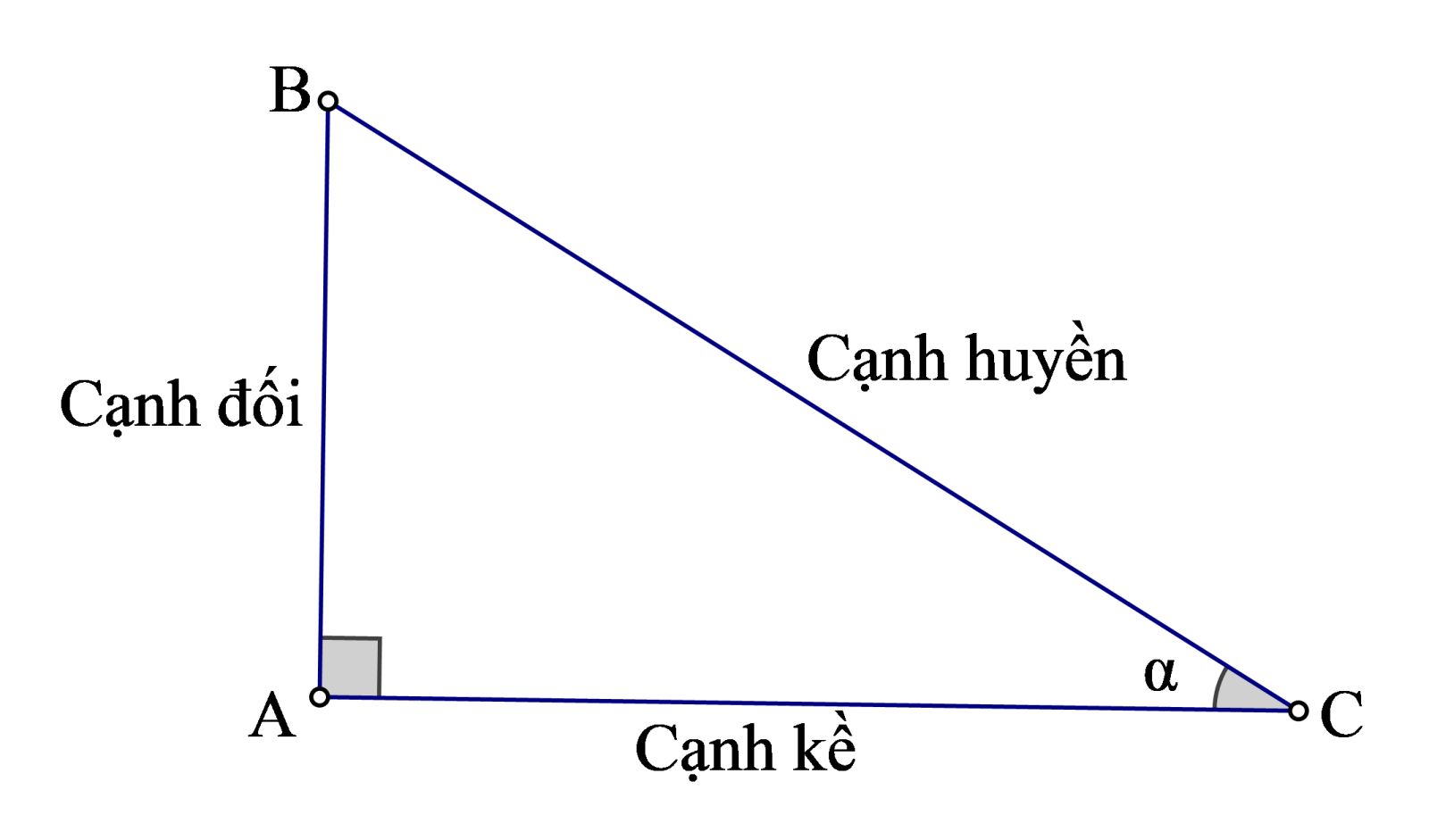
\(\sin \alpha =\frac{AB}{BC};\cos \alpha =\frac{AC}{BC};\tan \alpha =\frac{AB}{AC};\cot \alpha =\frac{AC}{AB}\)

+ Nếu \(\alpha\) là một góc nhọn thì \(0<\sin \alpha <1;0<\cos \alpha <1;\) \(\tan \alpha >0;\cot \alpha >0\)

        2. Với hai góc \(\alpha ,\beta \) mà \(\alpha +\beta ={{90}^{0}}\).

Ta có: \(\sin \alpha =\cos \beta ;\cos \alpha =\sin \beta ;\tan \alpha =\cot \beta ;\cot \alpha =\tan \beta \).

Nếu hai góc nhọn \(\alpha \) và \(\beta \) có \(\sin \alpha =\sin \beta \) hoặc \(\cos \alpha =\cos \beta \) thì \(\alpha =\beta \).

       3. \({{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1;tg\alpha .\cot g\alpha =1\).

       4. Với một số góc đặc biệt ta có: \(\sin {{30}^{0}}=\cos {{60}^{0}}=\frac{1}{2};\sin {{45}^{0}}=\cos {{45}^{0}}=\frac{\sqrt{2}}{2}\) \(\cos {{30}^{0}}=\sin {{60}^{0}}=\frac{\sqrt{3}}{2};\cot {{60}^{0}}=\tan {{30}^{0}}=\frac{1}{\sqrt{3}}\) \(\tan {{45}^{0}}=\cot {{45}^{0}}=1;\cot {{30}^{0}}=\tan {{60}^{0}}=\sqrt{3}\).

• Ví dụ 1. Biết \(\sin \alpha =\frac{5}{13}\). Tính \(\cos \alpha ,\tan \alpha \)0 và \(\cot \alpha\).

Giải:

                                                                                                                                               

Cách 1. Xét \(\Delta ABC\) vuông tại A.

Đặt \(\widehat{B}=\alpha \). Ta có: \(\sin \alpha =\frac{AC}{BC}=\frac{5}{13}\)

suy ra \(\frac{AC}{5}=\frac{BC}{13}=k\), do đó

\(AC=5k,BC=13k\). Tam giác ABC vuông tại A nên: \(A{{B}^{2}}=B{{C}^{2}}-A{{C}^{2}}={{\left( 13k \right)}^{2}}-{{\left( 5k \right)}^{2}}=144{{k}^{2}}\), suy ra \(AB=12k\).

Vậy \(\cos \alpha =\frac{AB}{BC}=\frac{12k}{13k}=\frac{12}{13}\); \(\tan \alpha =\frac{AC}{AB}=\frac{5k}{12k}=\frac{5}{12};\) \(\cot \alpha =\frac{AB}{AC}=\frac{12k}{5k}=\frac{12}{5}\).

Cách 2. Ta có \(\sin \alpha =\frac{5}{13}\) suy ra \({{\sin }^{2}}\alpha =\frac{25}{169}\), mà \({{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1\), do đó \({{\cos }^{2}}\alpha =1-{{\sin }^{2}}\alpha =1-\frac{25}{169}=\frac{144}{169}\), suy ra \(\cos \alpha =\frac{12}{13}\).

\(\tan \alpha =\frac{\sin \alpha }{\cos \alpha }=\frac{5}{13}:\frac{12}{13}=\frac{5}{13}.\frac{13}{12}=\frac{5}{12}\); \(\cot \alpha =\frac{\cos \alpha }{\sin \alpha }=\frac{12}{13}:\frac{5}{13}=\frac{12}{13}.\frac{13}{5}=\frac{12}{5}\).

Ở  cách giải thứ nhất ta biểu thị độ dài các cạnh của tam giác ABC theo đại lượng k rồi sử dụng định nghĩa tỉ số lượng giác của góc nhọn để tính \(\cos \alpha ,\tan \alpha ,\cot \alpha \).

Ở cách giải thứ hai, ta sử dụng giả thiết \(\sin \alpha =\frac{5}{13}\) để tính \({{\sin }^{2}}\alpha \) rồi tính \(\cos \alpha \) từ \({{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1\). Sau đó ta tính \(\tan \alpha \) và \(\cot \alpha \) qua \(\sin \alpha \) và \(\cos \alpha \).

 

• Ví dụ 2. Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết \(HD:HA=1:2\). Chứng minh rằng \(tgB.tgC=3\).

Giải:

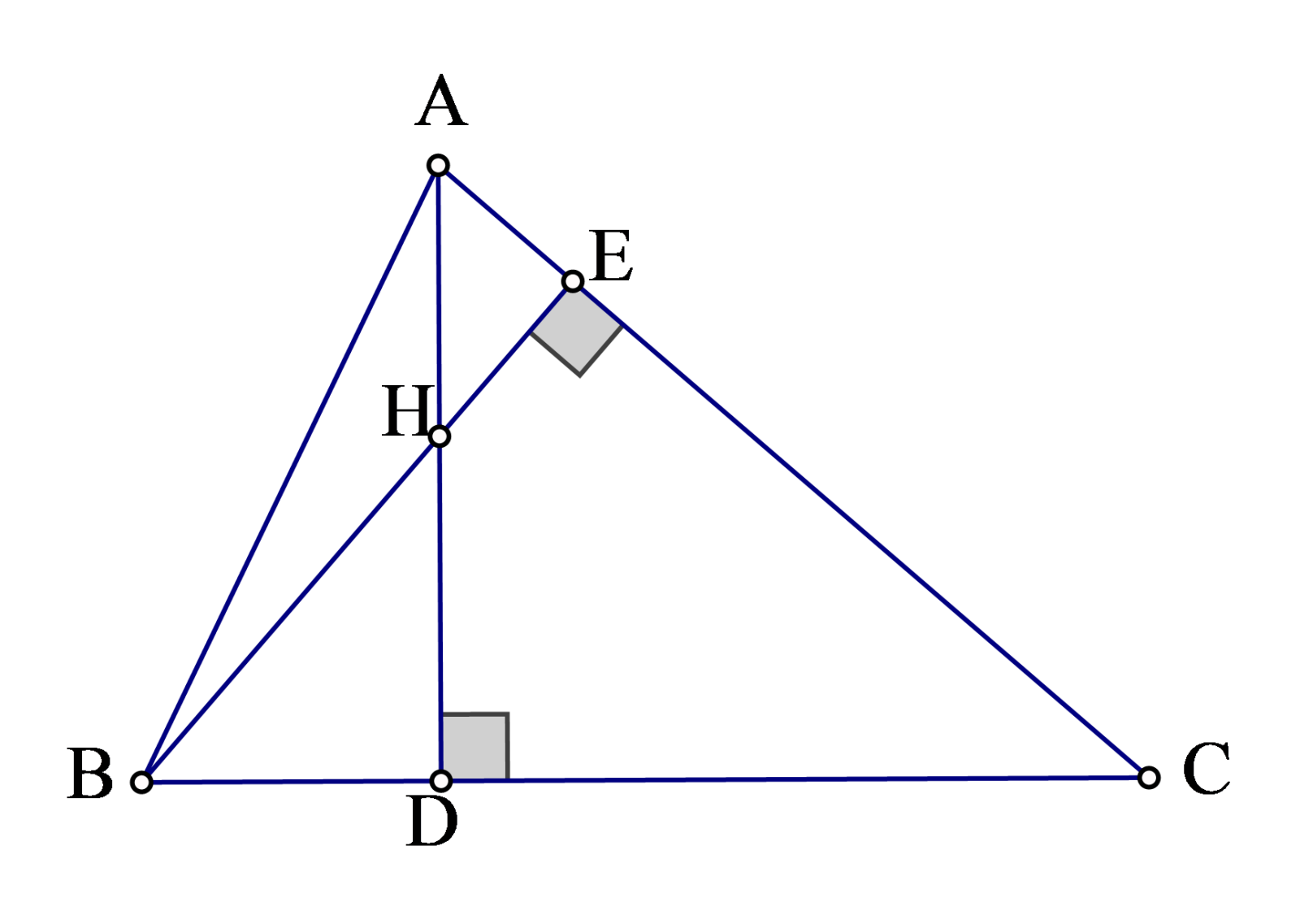
Ta có: \(tgB=\frac{AD}{BD};tgC=\frac{AD}{CD}\).

Suy ra \(\tan B.\tan C=\frac{A{{D}^{2}}}{BD.CD}\)   (1)

\(\widehat{HBD}=\widehat{CAD}\) (cùng phụ với \(\widehat{ACB}\); \(\widehat{HDB}=\widehat{ADC}={{90}^{0}}\).

Do đó \(\Delta BDH\sim \Delta ADC\) (g.g), suy ra \(\frac{DH}{DC}=\frac{BD}{AD}\), do đó \(BD.DC=DH.AD\)  (2). Từ (1) và (2) suy ra \(\tan B.\tan C=\frac{A{{D}^{2}}}{DH.AD}=\frac{AD}{DH}\)  (3). Theo giả thiết \(\frac{HD}{AH}=\frac{1}{2}\) suy ra \(\frac{HD}{AH+HD}=\frac{1}{2+1}\) hay \(\frac{HD}{AD}=\frac{1}{3}\), suy ra \(AD=3HD\). Thay vào (3) ta được: \(\tan B.\tan C=\frac{3HD}{DH}=3\).

 

• Ví dụ 3. Biết \(\sin \alpha .\cos \alpha =\frac{12}{25}\). Tính \(\sin \alpha ,\cos \alpha \).

Giải:

Biết \(\sin \alpha .\cos \alpha =\frac{12}{25}\). Để tính \(\sin \alpha ,\cos \alpha \) ta cần tính \(\sin \alpha +\cos \alpha \) rồi giải phương trình với ẩn là \(\sin \alpha \) hoặc \(\cos \alpha \).

Ta có: \({{\left( \sin \alpha +\cos \alpha  \right)}^{2}}={{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha +2\sin \alpha .\cos \alpha =1+2.\frac{12}{25}=\frac{49}{25}\). Suy ra \(\sin \alpha +\cos \alpha =\frac{7}{5}\) nên \(\sin \alpha =\frac{7}{5}-\cos \alpha \). Từ đó ta có: \(\cos \alpha \left( \frac{7}{5}-\cos \alpha  \right)=\frac{12}{25}\Leftrightarrow \frac{7}{5}\cos \alpha -{{\cos }^{2}}\alpha =\frac{12}{25}\) \(\Leftrightarrow 25{{\cos }^{2}}\alpha -35\cos \alpha +12=0\Leftrightarrow 5\cos \alpha \left( 5\cos \alpha -4 \right)-3\left( 5\cos \alpha -4 \right)=0\) \(\Leftrightarrow \left( 5\cos \alpha -4 \right)\left( 5\cos \alpha -3 \right)=0\). Suy ra \(\cos \alpha =\frac{4}{5}\) hoặc \(\cos \alpha =\frac{3}{5}\).

+ Nếu \(\cos \alpha =\frac{4}{5}\) thì \(\sin \alpha =\frac{12}{25}:\frac{4}{5}=\frac{3}{5}\).

+ Nếu \(\cos \alpha =\frac{3}{5}\) thì \(\sin \alpha =\frac{12}{25}:\frac{3}{5}=\frac{4}{5}\).

Vậy \(\sin \alpha =\frac{3}{5}\), \(\cos \alpha =\frac{4}{5}\) hoặc \(\sin \alpha =\frac{4}{5},\cos \alpha =\frac{3}{5}\).

 

---(Để xem đầy đủ nội dung chi tiết của tài liệu, các em vui lòng xem online hoặc đăng nhập để tải về máy)--- 

Trên đây là một phần trích dẫn nội dungCông thức tính tỉ số lượng giác của góc nhọn và bài tập áp dụng Toán 9 chi tiết nhất. Để xem toàn bộ nội dung các em đăng nhập vào trang HOC247.net để tải tài liệu về máy tính. Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.

Chúc các em học tốt!