Chuy├¬n ─æß╗ü tß╗ē lß╗ć thß╗ā t├Łch cß╗¦a c├Īc khß╗æi ─æa diß╗ćn to├Īn 12 ─æŲ░ß╗Żc hoc247 bi├¬n soß║Īn v├Ā tß╗Ģng hß╗Żp dŲ░ß╗øi ─æ├óy sß║Į hß╗ć thß╗æng tß║źt cß║Ż c├Īc b├Āi tß║Łp trß║»c nghiß╗ćm c├│ ─æ├Īp ├Īn nhß║▒m gi├║p bß║Īn ─æß╗Źc cß╗¦ng cß╗æ kiß║┐n thß╗®c l├Į thuyß║┐t v├Ā r├©n luyß╗ćn kß╗╣ n─āng giß║Żi b├Āi tß║Łp m├┤n To├Īn. Mß╗Øi c├Īc bß║Īn c├╣ng tham khß║Żo.
I. L├Ø THUYß║ŠT CHUNG
1. Hai khß╗æi ch├│p \(S.{{A}_{1}}{{A}_{2}}...{{A}_{n}}\) v├Ā \(S.{{B}_{1}}{{B}_{2}}...{{B}_{m}}\)c├│ chung ─æß╗ēnh \(S\) v├Ā hai mß║Ęt ─æ├Īy c├╣ng nß║▒m tr├¬n mß╗Öt mß║Ęt phß║│ng, ta c├│: \(\frac{{{V}_{S.{{A}_{1}}{{A}_{2}}...{{A}_{n}}}}}{{{V}_{S.{{B}_{1}}{{B}_{2}}...{{B}_{m}}}}}=\frac{{{S}_{{{A}_{1}}{{A}_{2}}...{{A}_{n}}}}}{{{S}_{{{B}_{1}}{{B}_{2}}...{{B}_{m}}}}}\)
2. Hai khß╗æi ch├│p tam gi├Īc \(S.ABC\) c├│ \({A}'\in SA,{B}'\in SB,C'\in SC\) ta c├│: \(\frac{{{V}_{S.A'B'C'}}}{{{v}_{S.ABC}}}=\frac{S{A}'}{SA}.\frac{S{B}'}{SB}.\frac{S{C}'}{SC}\)
3. Kiß║┐n thß╗®c cß║¦n nhß╗ø ─æß╗æi vß╗øi khß╗æi l─āng trß╗ź tam gi├Īc v├Ā khß╗æi hß╗Öp.
-
\({{V}_{{A}'.ABC}}=\frac{V}{3}\), \({{V}_{{A}'.BC{C}'{B}'}}=\frac{2V}{3}\).
-
\({{V}_{{A}'.ABD}}=\frac{V}{6}\), \({{V}_{BD{A}'{C}'}}=\frac{V}{3}\).
4. Mß╗Öt sß╗æ c├┤ng thß╗®c nhanh cho c├Īc trŲ░ß╗Øng hß╗Żp hay gß║Ęp
-
Tam gi├Īc \(ABC\) vu├┤ng tß║Īi \(A\) c├│ ─æŲ░ß╗Øng cao \(AH\) c├│ \(\frac{BH}{BC}={{\left( \frac{AB}{BC} \right)}^{2}},\) \(\frac{CH}{CB}={{\left( \frac{AC}{BC} \right)}^{2}}.\)
-
Mß║Ęt phß║│ng \(\left( \alpha \right)\) song song vß╗øi mß║Ęt ─æ├Īy cß╗¦a khß╗æi ch├│p \(S.{{A}_{1}}{{A}_{2}}...{{A}_{n}}\) cß║»t \(S{{A}_{k}}\) tß║Īi ─æiß╗ām \({{M}_{k}}\) thß╗Åa m├Żn \(\frac{S{{M}_{k}}}{S{{A}_{k}}}=p,\) ta c├│ \(\frac{{{V}_{S.{{M}_{1}}{{M}_{2}}...{{M}_{n}}}}}{{{V}_{S.{{A}_{1}}{{A}_{2}}...{{A}_{n}}}}}={{p}^{3}}.\)
-
H├¼nh l─āng trß╗ź tam gi├Īc \(ABC.{A}'{B}'{C}'\) c├│ \(\frac{AM}{A{A}'}=x,\frac{BN}{B{B}'}=y,\frac{CP}{C{C}'}=z\) c├│ \({{V}_{ABC.MNP}}=\frac{x+y+z}{3}V.\)
-
H├¼nh hß╗Öp \(ABCD.{A}'{B}'{C}'{D}'\) c├│ \(\frac{AM}{A{A}'}=x,\frac{BN}{B{B}'}=y,\frac{CP}{C{C}'}=z\). Mß║Ęt phß║│ng \(\left( MNP \right)\) cß║»t \(DD'\) tß║Īi \(Q\) th├¼ ta c├│ ─æß║│ng thß╗®c \(x+z=y+t\) vß╗øi \(t=\frac{DQ}{D{D}'}\) v├Ā \({{V}_{ABCD.MNPQ}}=\frac{x+y+z+t}{4}V.\)
-
H├¼nh ch├│p \(S.ABCD\) c├│ ─æ├Īy \(ABCD\) l├Ā h├¼nh b├¼nh h├Ānh v├Ā \(\frac{SM}{SA}=x,\frac{SN}{SB}=y,\frac{SP}{SC}=z\). Mß║Ęt phß║│ng \(\left( MNP \right)\) cß║»t \(SD\) tß║Īi \(Q\) th├¼ ta c├│ ─æß║│ng thß╗®c \(\frac{1}{x}+\frac{1}{z}=\frac{1}{y}+\frac{1}{t}\) vß╗øi \(t=\frac{SQ}{SD}\) v├Ā \({{V}_{S.MNPQ}}=\frac{1}{4}xyzt\left( \frac{1}{x}+\frac{1}{y}+\frac{1}{z}+\frac{1}{t} \right)V\).
-
─Éß╗ŗnh l├Ł Meneleus cho 3 ─æiß╗ām thß║│ng h├Āng \(\frac{MA}{MB}.\frac{NB}{NC}.\frac{PC}{PA}=1\) vß╗øi \(MNP\)l├Ā mß╗Öt ─æŲ░ß╗Øng thß║│ng cß║»t ba ─æŲ░ß╗Øng thß║│ng \(AB,BC,CA\) lß║¦n lŲ░ß╗Żt tß║Īi \(M,N,P.\)
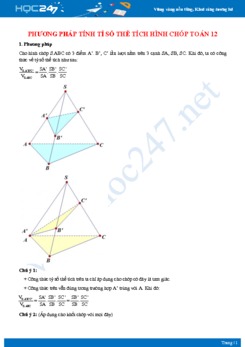
V├Ł dß╗ź: Cho h├¼nh ch├│p tß╗® gi├Īc ─æß╗üu \(S.ABCD\) c├│ cß║Īnh ─æ├Īy bß║▒ng \(a\), cß║Īnh b├¬n hß╗Żp vß╗øi ─æ├Īy mß╗Öt g├│c \(60{}^\circ \). Gß╗Źi \(M\) l├Ā ─æiß╗ām ─æß╗æi xß╗®ng cß╗¦a \(C\) qua \(D\), \(N\) l├Ā trung ─æiß╗ām \(SC.\) Mß║Ęt phß║│ng \(\left( BMN \right)\) chia khß╗æi ch├│p \(S.ABCD\) th├Ānh hai phß║¦n. Tß╗ē sß╗æ thß╗ā t├Łch giß╗»a hai phß║¦n (phß║¦n lß╗øn tr├¬n phß║¦n b├®) bß║▒ng:
A. \(\frac{7}{5}\).
B. \(\frac{1}{7}\).
C. \(\frac{7}{3}\).
D. \(\frac{6}{5}\).
HŲ░ß╗øng dß║½n giß║Żi:
Chß╗Źn A.
.png?enablejsapi=1)
Giß║Ż sß╗Ł c├Īc ─æiß╗ām nhŲ░ h├¼nh vß║Į.
\(E=SD\cap MN\Rightarrow E\) l├Ā trß╗Źng t├óm tam gi├Īc \(SCM\), \(DF\ \text{//}\ BC\Rightarrow F\) l├Ā trung ─æiß╗ām \(BM\).
Ta c├│:
\(\begin{align} & \left( \widehat{SD,\left( ABCD \right)} \right)=\widehat{SDO}=60{}^\circ \\ & \Rightarrow SO=\frac{a\sqrt{6}}{2} \\ \end{align}\), \(SF=\sqrt{S{{O}^{2}}+O{{F}^{2}}}=\frac{a\sqrt{7}}{2}\)
\(\Rightarrow d\left( O,\left( SAD \right) \right)=OH=h=\frac{a\sqrt{6}}{2\sqrt{7}};{{S}_{SAD}}=\frac{1}{2}SF.AD=\frac{{{a}^{2}}\sqrt{7}}{4}\)
\(\frac{{{V}_{MEFD}}}{{{V}_{MNBC}}}=\frac{ME}{MN}\cdot \frac{MF}{MB}\cdot \frac{MD}{MC}=\frac{1}{6}\)
\(\Rightarrow {{V}_{BFDCNE}}=\frac{5}{6}{{V}_{MNBC}}=\frac{5}{6}\cdot \frac{1}{3}\cdot d\left( M,\left( SAD \right) \right)\cdot \frac{1}{2}{{S}_{SBC}}=\frac{5}{18}\cdot 4h\cdot \frac{1}{2}{{S}_{SAD}}=\frac{5{{a}^{3}}\sqrt{6}}{72}\)
\({{V}_{S.ABCD}}=\frac{1}{3}SO.{{S}_{ABCD}}=\frac{{{a}^{3}}\sqrt{6}}{6}\Rightarrow {{V}_{SABFEN}}={{V}_{S.ABCD}}-{{V}_{BFDCNE}}=\frac{7{{a}^{3}}\sqrt{6}}{36}\cdot \)
Suy ra: \(\frac{{{V}_{SABFEN}}}{{{V}_{BFDCNE}}}=\frac{7}{5}\cdot \)
II. B├ĆI Tß║¼P
C├óu 1: Cho h├¼nh ch├│p\(S.ABC\).Tr├¬n cß║Īnh \(SA\) lß║źy c├Īc ─æiß╗ām \(M,N\) sao cho\(SM=MN=NA\).Gß╗Źi \(\left( \alpha \right),\left( \beta \right)\) l├Ā c├Īc mß║Ęt phß║│ng song song vß╗øi mß║Ęt phß║│ng \(\left( ABC \right)\) v├Ā lß║¦n lŲ░ß╗Żt ─æi qua\(M,N\). Khi ─æ├│ hai mß║Ęt phß║│ng \(\left( \alpha \right),\left( \beta \right)\) chia khß╗æi ch├│p ─æ├Ż cho th├Ānh 3 phß║¦n.Nß║┐u phß║¦n tr├¬n c├╣ng c├│ thß╗ā t├Łch l├Ā \(10\,d{{m}^{3}}\)t├Łch hai phß║¦n c├▓n lß║Īi lß║¦n lŲ░ß╗Żt l├Ā?
A. \(80\,d{{m}^{3}}\) v├Ā \(190\,d{{m}^{3}}\).
B. \(70\,d{{m}^{3}}\) v├Ā \(190\,d{{m}^{3}}\).
C. \(70\,d{{m}^{3}}\) v├Ā \(200\,d{{m}^{3}}\).
D. \(80\,d{{m}^{3}}\) v├Ā \(180\,d{{m}^{3}}\).
HŲ░ß╗øng dß║½n giß║Żi:
Chß╗Źn B
.png)
─Éß║Ęt \(V={{V}_{S.ABC}}\,,\,{{V}_{1}}={{S}_{S.MNP}}\) ta c├│:
\({{V}_{1}}=\frac{SM}{SA}.\frac{SP}{SB}.\frac{SQ}{SC}.V={{\left( \frac{1}{3} \right)}^{3}}V=\frac{1}{27}V\) \(\Rightarrow V=270\,d{{m}^{3}}\).
TŲ░ŲĪng tß╗▒ ta c├│ :
\({{V}_{1}}+{{V}_{2}}=\frac{SN}{SA}.\frac{SE}{SB}.\frac{SF}{SC}.V={{\left( \frac{2}{3} \right)}^{3}}V=\frac{8}{27}V=80\,d{{m}^{3}}\).
Do đó:\({{V}_{2}}=80-{{V}_{1}}=70\,d{{m}^{3}}\),\({{V}_{3}}=V-{{V}_{1}}-{{V}_{2}}=190\,d{{m}^{3}}\).
Chß╗Źn B.
C├óu 2: Cho h├¼nh ch├│p \(S.ABCD\) c├│ ─æ├Īy \(ABCD\) l├Ā h├¼nh b├¼nh h├Ānh v├Ā c├│ thß╗ā t├Łch bß║▒ng \(V\). Gß╗Źi \(M,N,P\) lß║¦n lŲ░ß╗Żt l├Ā c├Īc ─æiß╗ām tr├¬n c├Īc cß║Īnh \(SA,SB,SC\) sao cho \(\frac{SM}{SA}=\frac{1}{2},\frac{SN}{SB}=\frac{2}{3},\frac{SP}{SC}=\frac{1}{3}\). Mß║Ęt phß║│ng \(\left( MNP \right)\) cß║»t cß║Īnh \(SD\) tß║Īi ─æiß╗ām \(Q\). T├Łnh thß╗ā t├Łch khß╗æi ─æa diß╗ćn \(ABCD.MNPQ\).
A. \(\frac{5}{63}V\).
B. \(\frac{10}{63}V\).
C. \(\frac{53}{63}V\).
D. \(\frac{58}{63}V\).
HŲ░ß╗øng dß║½n giß║Żi:
Chß╗Źn D
.png)
─Éß║Ęt \(x=\frac{SM}{SA}=\frac{1}{2}\), \(y=\frac{SN}{SB}=\frac{2}{3}\), \(z=\frac{SP}{SC}=\frac{1}{3}\), \(t=\frac{SQ}{SD}\).
Ta c├│ \(\frac{1}{x}+\frac{1}{z}=\frac{1}{y}+\frac{1}{t}\Rightarrow 2+3=\frac{3}{2}+\frac{1}{t}\Leftrightarrow t=\frac{2}{7}\).
Do đó \({{V}_{S.MNPQ}}={{V}_{S.MNP}}+{{V}_{S.PQM}}=xyz.\frac{1}{2}V+zxt.\frac{1}{2}V=\frac{1}{2}xz\left( y+t \right)V=\frac{5}{63}V\).
Suy ra \({{V}_{ABCD.MNPQ}}=\left( 1-\frac{5}{63} \right)V=\frac{58}{63}V\).
C├óu 3: Cho khß╗æi ch├│p \(S.ABCD\) c├│ ─æ├Īy l├Ā h├¼nh chß╗» nhß║Łt, \(AB=\sqrt{3}a\), \(AD=a\), \(SA\) vu├┤ng g├│c vß╗øi ─æ├Īy v├Ā
\(SA=a\). Mß║Ęt phß║│ng \(\left( \alpha\right)\) qua \(A\) vu├┤ng g├│c vß╗øi \(SC\) cß║»t \(SB\), \(SC\), \(SD\) lß║¦n lŲ░ß╗Żt tß║Īi \(M\), \(N\), \(P\). T├Łnh thß╗ā t├Łch khß╗æi ch├│p \(S.AMNP\).
A. \(\frac{3\sqrt{3}{{a}^{3}}}{40}\).
B. \(\frac{\sqrt{3}{{a}^{3}}}{40}\).
C. \(\frac{\sqrt{3}{{a}^{3}}}{10}\).
D. \(\frac{\sqrt{3}{{a}^{3}}}{30}\).
HŲ░ß╗øng dß║½n giß║Żi:
Chß╗Źn B
.png)
Ta c├│ \(SC\bot \left( \alpha \right)\Rightarrow SC\bot AM,SC\bot AN,SC\bot AP\).
Mß║Ęt kh├Īc \(CB\bot \left( SAB \right)\Rightarrow AM\bot CB\Rightarrow AM\bot \left( SBC \right)\Rightarrow AM\bot SB\). TŲ░ŲĪng tß╗▒ ta c├│ \(AP\bot SD\).
Thß╗ā t├Łch khß╗æi ch├│p ban ─æß║¦u l├Ā \(V=\frac{1}{3}\sqrt{3}{{a}^{2}}.a=\frac{\sqrt{3}{{a}^{3}}}{3}\).
T├Łnh c├Īc tß╗ē sß╗æ \(x=\frac{SA}{SA}=1\), \(y=\frac{SM}{SB}={{\left( \frac{SA}{SB} \right)}^{2}}=\frac{{{a}^{2}}}{{{a}^{2}}+3{{a}^{2}}}=\frac{1}{4}\),
\(z=\frac{SN}{SC}={{\left( \frac{SA}{SC} \right)}^{2}}=\frac{{{a}^{2}}}{{{a}^{2}}+3{{a}^{2}}+{{a}^{2}}}=\frac{1}{5}\), \(t=\frac{SP}{SD}={{\left( \frac{SA}{SD} \right)}^{2}}=\frac{{{a}^{2}}}{{{a}^{2}}+{{a}^{2}}}=\frac{1}{2}\).
Vß║Ły \({V}'=\frac{xyzt}{4}\left( \frac{1}{x}+\frac{1}{y}+\frac{1}{z}+\frac{1}{t} \right)V=\frac{3}{40}V=\frac{\sqrt{3}{{a}^{3}}}{40}\).
C├óu 4: Cho khß╗æi ch├│p \(S.ABCD\) c├│ thß╗ā t├Łch \(V\) v├Ā ─æ├Īy l├Ā h├¼nh b├¼nh h├Ānh. ─Éiß╗ām \({S}'\) thß╗Åa m├Żn \(\overrightarrow{S{S}'}=k\overrightarrow{DC}\,\left( k>0 \right)\). Biß║┐t thß╗ā t├Łch phß║¦n chung cß╗¦a hai khß╗æi ch├│p \(S.ABCD\)v├Ā \({S}'.ABCD\) l├Ā \(\frac{7}{25}V\). T├¼m \(k\).
A. \(k=9\).
B. \(k=6\).
C. \(k=11\).
D. \(k=4\).
HŲ░ß╗øng dß║½n giß║Żi:
Chß╗Źn D
Ta có \(AB\)//\(CD\)//\(S{S}'\) nên \({B}'={S}'A\cap SB,{C}'={S}'D\cap SC\).
Theo Thales ta c┼®ng c├│
\(\frac{{B}'S}{{B}'B}=\frac{{C}'S}{{C}'C}=\frac{{S}'S}{DC}=k\Rightarrow \frac{S{B}'}{SB}=\frac{S{C}'}{SC}=\frac{k}{k+1},t=\frac{SD}{SD}=1\).
Do đó \({{V}_{S.AD{C}'{B}'}}=\frac{1}{4}.1.1.\frac{k}{k+1}.\frac{k}{k+1}\left( \frac{1}{1}+\frac{1}{1}+\frac{1}{\frac{k}{k+1}}+\frac{1}{\frac{k}{k+1}} \right)V=\frac{{{k}^{2}}\left( 2k+1 \right)}{2k{{\left( k+1 \right)}^{2}}}V\).
Vß║Ły thß╗ā t├Łch phß║¦n chung l├Ā \({V}'=V-{{V}_{S.AD{C}'{B}'}}=\left( 1-\frac{{{k}^{2}}\left( 2k+1 \right)}{2k{{\left( k+1 \right)}^{2}}} \right)V=\frac{7}{25}V\Leftrightarrow k=4\,\left( k>0 \right)\).
C├óu 5: Cho h├¼nh ch├│p \(S.ABC\) c├│ tß║źt cß║Ż c├Īc cß║Īnh ─æß╗üu bß║▒ng \(a\). Mß╗Öt mß║Ęt phß║│ng \(\left( P \right)\) song song vß╗øi mß║Ęt ─æ├Īy \(\left( ABC \right)\) cß║»t c├Īc cß║Īnh \(SA\), \(SB\), \(SC\) lß║¦n lŲ░ß╗Żt tß║Īi \(M\), \(N\), \(P\). T├Łnh diß╗ćn t├Łch tam gi├Īc \(MNP\) biß║┐t \(\left( P \right)\) chia khß╗æi ch├│p ─æ├Ż cho th├Ānh hai khß╗æi ─æa diß╗ćn c├│ thß╗ā t├Łch bß║▒ng nhau.
A. \({{S}_{\Delta MNP}}=\frac{{{a}^{2}}.\sqrt{3}}{8}\).
B. \({{S}_{\Delta MNP}}=\frac{{{a}^{3}}.\sqrt{3}}{16}\).
C. \({{S}_{\Delta MNP}}=\frac{{{a}^{2}}.\sqrt{3}}{4\sqrt[3]{2}}\)
D. \({{S}_{\Delta MNP}}=\frac{{{a}^{2}}.\sqrt{3}}{4\sqrt[3]{4}}\).
HŲ░ß╗øng dß║½n giß║Żi:
Chß╗Źn D.
.png)
\(\frac{{{V}_{S.MNP}}}{{{V}_{S.ABC}}}=\frac{SM}{SA}.\frac{SN}{SB}.\frac{SP}{SC}={{\left( \frac{SM}{SA} \right)}^{3}}\text{ }\left( 1 \right)\)
Theo b├Āi ra: \(\frac{{{V}_{S.MNP}}}{{{V}_{S.ABC}}}=\frac{1}{2}\text{ }\left( 2 \right)\)
Từ \(\left( 1 \right)\), \(\left( 2 \right)\) ta có \({{\left( \frac{SM}{SA} \right)}^{3}}=\frac{1}{2}\)\(\Leftrightarrow \frac{SM}{SA}=\frac{1}{\sqrt[3]{2}}\)
Lß║Īi c├│: \(\frac{{{V}_{S.MNP}}}{{{V}_{S.ABC}}}=\frac{\frac{1}{3}d\left( S,\left( MNP \right) \right).{{S}_{\Delta MNP}}}{\frac{1}{3}d\left( S,\left( ABC \right) \right).{{S}_{\Delta ABC}}}\text{=}\frac{1}{2}\text{ }\left( 3 \right)\)
M├Ā \(\frac{d\left( S,\left( MNP \right) \right)}{d\left( S,\left( ABC \right) \right)}\text{=}\frac{SM}{SA}=\frac{1}{\sqrt[3]{2}}\text{ }\left( 4 \right)\)
Tß╗½ \(\left( 3 \right)\), \(\left( 4 \right)\) ta c├│ ─æŲ░ß╗Żc \(\frac{{{S}_{\Delta MNP}}}{{{S}_{\Delta ABC}}}\text{=}\frac{\sqrt[3]{2}}{2}\)\(\Rightarrow {{S}_{\Delta MNP}}\text{=}\frac{\sqrt[3]{2}}{2}{{S}_{\Delta ABC}}=\frac{\sqrt[3]{2}}{2}.\frac{{{a}^{2}}.\sqrt{3}}{4}=\frac{{{a}^{2}}.\sqrt{3}}{4.\sqrt[3]{4}}\)
...
--(Nß╗Öi dung ─æß║¦y ─æß╗¦, chi tiß║┐t vui l├▓ng xem tß║Īi online hoß║Ęc ─æ─āng nhß║Łp ─æß╗ā tß║Żi vß╗ü m├Īy)--
Tr├¬n ─æ├óy l├Ā mß╗Öt phß║¦n tr├Łch ─æoß║Īn nß╗Öi dung Chuy├¬n ─æß╗ü tß╗ē lß╗ć thß╗ā t├Łch cß╗¦a c├Īc khß╗æi ─æa diß╗ćn to├Īn 12ŌĆŗŌĆŗ. ─Éß╗ā xem th├¬m nhiß╗üu t├Āi liß╗ću tham khß║Żo hß╗»u ├Łch kh├Īc c├Īc em chß╗Źn chß╗®c n─āng xem online hoß║Ęc ─æ─āng nhß║Łp v├Āo trang hoc247.net ─æß╗ā tß║Żi t├Āi liß╗ću vß╗ü m├Īy t├Łnh.
Hy vß╗Źng t├Āi liß╗ću n├Āy sß║Į gi├║p c├Īc em hß╗Źc sinh ├┤n tß║Łp tß╗æt v├Ā ─æß║Īt th├Ānh t├Łch cao trong hß╗Źc tß║Łp.
C├Īc em quan t├óm c├│ thß╗ā tham khß║Żo th├¬m c├Īc t├Āi liß╗ću c├╣ng chuy├¬n mß╗źc:
-
PhŲ░ŲĪng ph├Īp t├Łnh tß╗ē sß╗æ thß╗ā t├Łch h├¼nh ch├│p To├Īn 12
-
L├Į thuyß║┐t v├Ā b├Āi tß║Łp vß╗ü t├Łnh thß╗ā t├Łch h├¼nh ch├│p To├Īn 12
Ch├║c c├Īc em hß╗Źc tß╗æt!
T├Āi liß╗ću li├¬n quan
TŲ░ liß╗ću nß╗Ģi bß║Łt tuß║¦n
- Xem thêm