Bộ 5 đề thi thử vào lớp 10 môn Toán năm 2022-2023 có đáp án Trường THCS Lê Văn Tám

TRƯỜNG THCS LÊ VĂN TÁM

ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN NĂM HỌC 2022 – 2023 Thời gian: 120 phút

Câu 1.(1,5 điểm) Cho \(\left( P \right):y=2{{x}^{2}}\) và \(\left( D \right):y=3x-1\).

a) Vẽ \(\left( P \right)\) và \(\left( D \right)\) trên cùng một hệ trục tọa độ.

b) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( D \right)\) bằng phép tính.

Câu 2.(1 điểm) Cho phương trình \({{x}^{2}}-10x-8=0\) có hai nghiệm \({{x}_{1}},{{x}_{2}}\). Không giải phương trình hãy tính giá trị của biểu thức \(A=\left( {{x}_{1}}-{{x}_{2}} \right)\left( x_{1}^{2}-x_{2}^{2} \right)\).

Câu 3.(1 điểm) Các nhà khoa học về thống kê đã thiết lập được hàm số sau: \(A\left( t \right)=0,08t+19,7\). Trong đó \(A\left( t \right)\) là độ tuổi trung bình các phụ nữ kết hôn lần đầu của thế giới; t là số năm kết hôn, với gốc thời gian là 1950. Hãy tính độ tuổi trung bình các phụ nữ kết hôn lần đầu lần lượt vào các năm 1950, 2000,2018¸ 2020 (làm tròn đến chữ số thập phân thứ hai).

Câu 4.(1 điểm) Một trường học có tổng số giáo viên là 80 người, hiện tại tuổi trung bình của giáo viên là 35 tuổi .Trong đó, tuổi tuổi trung bình của giáo viên nữ là 32 tuổi và tuổi trung bình của giáo viên nam là 38 tuổi. Hỏi 3 trường đó có bao nhiêu giáo viên nam, bao nhiêu giáo viên nữ?

Câu 5.(1 điểm) Bé An sống trong gia đình ba thế hệ gồm ông bà nội, ba mẹ, bé An và em trai. Chủ nhật vừa rồi cả gia đình đi xem phim. Biết giá vé cho trẻ em (vé của bé An và em trai) được giảm giá 50%; vé người cao tuổi được giảm giá 25% (vé của ông bà nội ). Vé của ba mẹ không được giảm giá. Ông nội bé An, người phải trả giá vé là $60$60 nghìn đồng, đang trả tiền cho mọi người. Hỏi ông nội phải trả bao nhiêu tiền?

Câu 6.(1 điểm) Theo năm Dương lịch, chu kỳ Trái Đất quay quanh Mạt Trời là 365 ngày và ngày (tức là 365,25 ngày). Khi đó, \(\frac{1}{4}\) ngày này sẽ được tích lũy trong vòng 4 năm nên theo năm Dương lịch thì cứ 4 năm lại có 1 năm là năm nhuận vào các năm chia hết cho 4 (tháng 2 của năm này sẽ có 29 ngày thay vì có 28 ngày như các năm không nhuận Dương lịch).

Tuy nhiên, vẫn có một số ngoại lệ đối với nguyên tắc trên vì có khi một năm Dương lịch lại ngắn hơn 365,25 ngày nên với những năm có hai chữ số 0 ở cuối thì năm đó phải chia hết cho $400 mới là năm nhuận Dương lịch.

a) Từ năm 1900 đến năm 2000 có bao nhiêu năm nhuận Dương lịch? Vì sao?

b) Một nhà hộ sinh trong tháng 2 năm 2021 có 29 em bé chào đời là con của 29 gia đình khác nhau. Có thể chắc chắn rằng có ít nhất 2 em bé chào đời cùng ngày hay không? Vì sao?

Câu 7.(1,0 điểm) Thớt là một dụng cụ sử dụng trong bếp của mỗi gia đình để thái, chặt, .... Một cái thớt hình trụ có đường kính đáy 22cm, cao 4cm.

a) Tính tổng diện tích hai mặt thớt (làm tròn đến \(c{{m}^{2}}\) ).

b) Cho biết loại gỗ làm thớt có khối lượng \(500kg/{{m}^{3}}\). Hỏi thớt nặng bao nhiêu gam? Công thức tính thể tích hình trụ là \(V=S.h\) (S là diện tích đáy và h là chiều cao hình trụ).

Câu 8.(2,5 điểm) Cho \(\Delta ABC\) có 3 góc nhọn nội tiếp đường tròn \(\left( O;R \right)\). Gọi M,P,Q lần lượt là điểm chính giữa các cung \(\overset\frown{BC}\), \(\overset\frown{CA}\) và \(\overset\frown{AB}\). Gọi T là giao điểm của BP và CQ. Đường thẳng vuông góc với BP tại B và đường thẳng vuông góc với CQ tại C cắt nhau ở I. Vẽ đường kính MN của \(\left( O \right)\). Gọi K là hình chiếu của I trên AB.

a) Chứng minh: \(\Delta AKI\,\,\Delta NCM\) và tứ giác BICT nội tiếp.

b) PQ cắt AC tại H, MQ cắt BC tại V. Chứng minh 3 điểm H,T,V thẳng hàng.

c) Gọi OI=d,IK=r. Chứng minh: \({{d}^{2}}={{R}^{2}}+2Rr\).

ĐÁP ÁN

a) Vẽ đồ thị \(\left( P \right)\) và \(\left( d \right)\) trên cùng hệ trục tọa độ.

BGT

Đồ thị

Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép tính.

Phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right): \Leftrightarrow 2{x^2} - 3x + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 1\\
x = \frac{1}{2}
\end{array} \right.{\rm{ }}\)

Thay x=1 vào \(y=2{{x}^{2}}\), ta được: \(y={{2.1}^{2}}=2\).

Thay \(x=\frac{1}{2}\) vào \[y=2{{x}^{2}}\], ta được: \(y=2{{\left( \frac{1}{2} \right)}^{2}}=\frac{1}{2}\).

Vậy \(\left( 1;\,\,2 \right)\), \(\left( \frac{1}{2};\,\,\frac{1}{2} \right)\) là hai giao điểm cần tìm.

---(Để xem tiếp nội dung của đề thi số 1 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS VĂN TÁM- ĐỀ 02

Câu 1.(1,5 điểm). Cho \(\left( P \right):y=-{{x}^{2}}\) và đường thẳng \(\left( d \right):y=3x-4\).

a) Vẽ đồ thị \(\left( P \right)\) và \(\left( d \right)\) trên cùng mặt phẳng tọa độ.

b) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép tính.

Câu 2. (1 điểm). Cho phương trình \(2{{x}^{2}}-5x=-3\) có 2 nghiệm là \({{x}_{1}},{{x}_{2}}\). Không giải phương trình, hãy tính giá trị của biểu thức \(A=\left( {{x}_{1}}+3{{x}_{2}} \right)\left( {{x}_{2}}+3{{x}_{1}} \right)\).

Câu 3. (1 điểm). Tổng điều tra dân số và nhà ở năm 2019 được tiến hành vào thời điểm 0 giờ ngày 1/4/2019 theo Quyết định số 772/QĐ-TTg ngày 26/6/2018 của Thủ tướng Chính phủ. Đây là cuộc Tổng điều tra dân số và nhà ở lần thứ năm ở Việt Nam kể từ khi đất nước thống nhất vào năm 1975. Theo kết quả của cuộc tổng điều tra nói trên, tổng dân số của Việt Nam là 96.208.984 người, trong đó nam ít hơn nữ 446.862 người và dân tộc Kinh chiếm 85,3% dân số cả nước.

a) Dân tộc Kinh có bao nhiêu người (làm tròn đến hàng đơn vị)?

b) Tính số nam và số nữ của Việt Nam.

Câu 4.(1 điểm).

Một xí nghiệp cần bán thanh lý b sản phẩm. Số sản phẩm y còn lại sau x ngày bán được xác định bởi hàm số: y=ax+b có đồ thị như bên.

a) Hãy dựa vào đồ thị xác định a, b và hàm số y.

b) Xí nghiệp cần bao nhiêu ngày để bán hết số sản phẩm cần thanh lý?

Câu 5.(1 điểm). Các bạn học sinh của lớp 9A dự định đóng góp một số tiền để mua tặng cho mỗi em ở Mái ấm tình thương ba món quà (giá tiền các món quà đều như nhau). Khi các bạn đóng đủ số tiền dự trù thì Mái ấm đã nhận chăm sóc thêm 9 em và giá tiền mỗi món quà lại tăng thêm 5% nên số tiền có được vừa đủ để tặng mỗi em hai món quà. Hỏi có bao nhiêu em ở Mái ấm lúc tặng quà?

Câu 6. (1 điểm).

Coi cả Trái Đất và Mặt Trăng đều có dạng hình cầu và biết bán kính của Trái Đất là khoảng \(6371\text{ }km\), bán kính của mặt trăng là khoảng \(1737\text{ }km\).

a) Hãy tính diện tích bề mặt của Trái Đất và diện tích bề mặt của Mặt Trăng.

b) Biết 70,8% diện tích bề mặt Trái Đất là nước. Hãy tính phần diện tích này?

(Làm tròn kết quả đến hàng triệu)

Câu 7.(1 điểm). Giá của một mặt hàng là 800.000 đồng. Nếu bán mặt hàng này với giá bằng một nửa giá niêm yết thì lợi nhuận là 20%. Hỏi phải bán với giá bao nhiêu thì được lợi nhuận 60%?

Câu 8.(2,5 điểm) Cho tam giác ABC nhọn \(\left( AB < AC \right)\) nội tiếp đường tròn \(\left( O \right)\) có ba đường cao AD, BE, CF cắt nhau tại H.

a) Chứng minh AEHF và ABDE là các tứ giác nội tiếp.

b) Đường thẳng EF cắt đường tròn \(\left( O \right)\) tại các điểm M, N (M thuộc cung nhỏ AB). Kẻ đường kính AK của đường tròn \(\left( O \right)\). Chứng minh tia EB là tia phân giác của góc DEF và \(\Delta KMN\) cân.

c) Đường trung trực của CE cắt MK tại Q. Chứng minh MA là tiếp tuyến của \(\left( MEC \right)\)  và OQ vuông góc MC.

---(Để xem tiếp nội dung của đề thi số 2 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS VĂN TÁM- ĐỀ 03

Câu 1.( 1,5 điểm ). Cho Parabol \(\left( P \right):y=\frac{1}{2}{{x}^{2}}\) và đường thẳng \((d):y=x+4\)

a) Vẽ đồ thị hàm số \((P)\) và \((d)\) trên cùng hệ trục tọa độ.

b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.

Câu 2.( 1,0 điểm ). Cho phương trình \({{x}^{2}}-5x-2=0\) có hai nghiệm là \({{x}_{1}},{{x}_{2}}\). Không giải phương trình, hãy tính giá trị của biểu thức: \(A={{x}_{1}}^{2}+{{x}_{2}}^{2}+{{x}_{1}}+{{x}_{2}}\).

Câu 3.( 0,75 điểm ).Một năm bình thường sẽ có 12 tháng và  365 ngày. Khi một năm có số ngày hoặc số trong tăng lên (theo Dương lịch hoặc theo Âm lịch) thì sẽ được gọi là năm nhuận, trong đó có những ngày nhuận vào tháng nhuận. Năm nhuận là năm có 29 ngày tháng 2 Dương Lịch (không nhuận là 28 ngày). Cách tính năm nhuận theo Dương lịch là những năm dương lịch nào chia hết cho 4 thì đó là năm nhuận.

Ví dụ: 2016 chia hết cho 4 nên năm 2016 là năm nhuận.

Ngoài ra, đối với thế kỷ (những năm có 2 số cuối là số 0) thì ta sẽ lấy số năm đó chia cho 400, nếu như chia hết thì đó sẽ là năm nhuận (hoặc hai số đầu trong năm chia hết cho 4).

Vídụ: 1600 và 2000 là các năm nhuận nhưng 1700, 1800 và 1900 không phải năm nhuận.

a) Em hãy dùng quy tắc trên để xác định Năm 2022 có phải là năm nhuận dương lịch không?

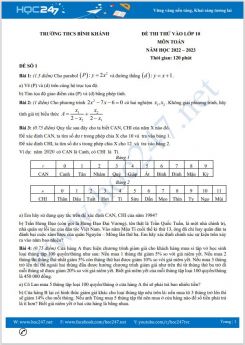
b) Bạn Hòa nhớ rằng sinh nhật lần thứ 15 của bạn vào ngày 2/6/2022 là ngày thứ năm. Bạn thắc mắc ngày mình sinh ra là ngày thứ mấy? Em hãy giúp bạn giải đáp thắc mắc đó.

Câu 4.(0,75 điểm).Một xe ôtô chuyển động theo hàm số \(S=30t+4{{t}^{2}}\), trong đó S (km) là quãng đường xe đi được trong thời gian t (giờ); t là thời gian chuyển động của tính từ lúc 7h00 sáng. Xem như xe chuyển động đều trên một đoạn đường thẳng và không nghỉ.

a) Hỏi từ lúc 7h30 phút đến lúc 8h15 phút đã đi được quãng đường dài bao nhiêu km?

b) Đến lúc mấy giờ thì xe đi được quãng đường dài 34km (tính từ lúc 7h00)?

Câu 5.(1,0 điểm).Mộtngườimua 3 đôigiàyvớihìnhthứckhuyếnmãinhưsau: Nếu bạn một đôi giày và mức giá thông thường, bạn sẽ được giá giảm 30% khi mua đôi thứ hai, và một đôi thứ ba về một nửa giá ban đầu. Bạn Anh đã trả 1.320.000 cho 3 đôi giày.

a) Giá ban đầu của một đôi giày là bao nhiêu?

b) Nếu cửa hàng đưa ra hình thức khuyến mãi thứ là giảm 20% mỗi đôi giày. Bạn Anh nên chọn hình thức khuyến mãi nào nếu mua ba đôi giày.

Câu 6. (1,0 điểm).Đổ nước vào một chiếc thùng hình trụ có bán kính đáy là 20 cm. Nghiêng thùng cho mặt nước chạm vào miệng cốc và đáy cốc (như hình vẽ) thì mặt nước tạo với đáy cốc một góc \(30{}^\circ \).

a) Tính chiều cao của chiếc thùng hình trụ.

b) Tính thể tích của chiếc thùng?

 (Kết quả làm tròn hai chữ số thập phân)

Câu 7.(1,0 điểm).Một đoàn y tế của Bệnh viện Chợ Rẫy, TP HCM gồm các bác sĩvà y tá tăng cường về tỉnh Cà Mau để khám chữa bệnh cho người dân trong tỉnh. Đoàn gồm 135 người và có tuổi trung bình là 40 tuổi. Tính số bác sĩ và y tá biết tuổi trung bình của các bác sĩ là 50 tuổi và tuổi trung bình của các y tá là 35 tuổi.

Câu 8.(3,0 điểm).Từ điểm A ở ngoài đường tròn tâm O, vẽ tiếp tuyến AB, AC với (O) (B, C là hai tiếp điểm). Vẽ cát tuyến AEF với (O) sao cho AE < AF và tia AF nằm giữa tia OA và tia OC. Gọi D là trung điểm của EF.

a) Chứng minh tứ giác AODC nội tiếp.

b) Gọi K là giao điểm của AF và BC. Chứng minh \(AD.AK\text{ }=\text{ }AE.AF.\)

c) Đường thẳng OD cắt các tia AB, AC lần lượt tại hai điểm M và N. Đường thẳng vuông góc với MN tại O cắt BC tại I, AI cắt MN tại H. Chứng minh H là trung điểm của MN.

---(Để xem tiếp nội dung của đề thi số 3 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS VĂN TÁM- ĐỀ 04

Bài 1: Cho Parabol (P): \(y=-\frac{{{x}^{2}}}{2}\) và đường thẳng (d): y = 3x + 4.

a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.

b) Tìm tọa độ giao điểm của (P) và (d) bằng phép toán.

Bài 2: Cho phương  trình: 5x2 – 9x – 14 = 0 có hai nghiệm x1, x2 . Không giải phương  trình, hãy tính giá trị của biểu thức: \(A=\frac{2{{x}_{1}}}{{{x}_{2}}}+\frac{2{{x}_{2}}}{{{x}_{1}}}\).

Bài 3: Hệ thống Định vị Toàn cầu (tiếng Anh: Global Positioning system – GPS) là hệ thống xác định vị trí trên mặt đất của các vật dựa trên vị trí của các vệ tinh nhân tạo trong không gian. Trong cùng một thời điểm, tọa độ của một điểm trên mặt đất sẽ được xác định nếu xác định được khoảng cách từ điểm đó đến ít nhất ba vệ tinh.

Quan sát hình trên, cho biết khoảng cách từ vệ tinh I đến tàu thủy T là 21000 km, đến xe hơi X là 21200km, góc hợp bởi mặt đất và đường nối vệ tinh với tàu thủy là 300, góc hợp bởi mặt đất và đường nối vệ tinh với xe hơi màu đỏ là 450. IH là đoạn vuông  góc từ vệ tinh đến mặt đất. Tính khoảng cách giữa tàu thủy và xe hơi được đo bởi vệ tinh I.

Bài 4: Nhà trường tổ chức cho 180 học sinh khối lớp 9 đi tham quan, nếu dùng xe lớn thì số xe dùng sẽ ít hơn xe nhỏ 2 chiếc, biết mỗi xe lớn chứa nhiều hơn mỗi xe nhỏ là 15 học sinh. Tìm số xe lớn đưa học sinh tham quan?

Bài 5: Kết quả của sự nóng dần lên của trái đất là băng tan trên một dòng sông bị đóng băng. Mười hai năm sau khi băng tan, những thực vật nhỏ, được gọi là Địa y, bắt đầu phát triển trên đá. Mỗi nhóm địa y phát triển trên một khoảng đất hình tròn.

Mối quan hệ giữa đường kính d tính bằng mi – li – met (mm) của hình tròn và tuổi t của Địa y có thể biểu diễn tương đối theo công thức: \(d=7\sqrt{t-12};\,\,(t\ge 12)\) 

a) Em hãy sử dụng công thức trên để tính đường kính của một nhóm Địa y, 16 năm sau khi băng tan.

b) An đo đường kính của một nhóm địa y và thấy có số đo là 35mm. Với kết quả trên thì băng đã tan cách đó bao nhiêu năm?

Bài 6:

Trong phòng học có một số ghế dài. Nếu xếp mỗi ghế 3 học sinh thì thừa ra 4 học sinh không có chỗ. Nếu xếp mỗi ghế 4 học sinh thì thừa ra 2 ghế. Hỏi có bao nhiêu ghế và bao nhiêu học sinh?

 Bài 7:

Cho đường tròn (O; R) có đường kính AB cố định. Vẽ đường kính MN của đường tròn (O; R) (M khác A, M khác B). Tiếp tuyến của đường tròn (O; R) tại B cắt các đường thẳng AM, AN lần lượt tại các điểm Q, P.

a) Chứng minh tứ giác AMBN là hình chữ nhật.

b) Chứng minh bốn điểm M, N, P, Q cùng thuộc một đường tròn.

c) Gọi E là trung điểm của BQ. Đường thẳng vuông góc với OE tại O cắt PQ tại điểm F. Chứng minh F là trung điểm của BP và ME // NF.

---(Để xem tiếp nội dung của đề thi số 4 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS VĂN TÁM- ĐỀ 05

Bài 1. Cho (P):\(y=-\frac{{{x}^{2}}}{2}\) và (d): \(y=x-4\)

a) Vẽ đồ thị (P), (d) trên cùng mặt phẳng tọa độ Oxy.

b) Tìm tọa độ giao điểm của (P) và (d).

Bài 2: Gọi x1, x2 là hai nghiệm của phương trình: x2 + 4x – 1 = 0.

Không giải phương trình, hãy tính giá trị của biểu thức: \(\text{A= }\frac{{{x}_{\text{1}}}}{{{x}_{\text{2}}}}+\frac{{{x}_{2}}}{{{x}_{1}}}+\frac{5}{2}\) 

Bài 3. Một hình chữ nhật có kích thước  cm. Người ta tăng mỗi kích thước của hình chữ nhật thêm  cm. Khi đó, chu vi P của hình chữ nhật được cho bởi hàm số bậc nhất

a) Cho biết hàm số đồng biến hay nghịch biến trên R? Vì sao?

b) Hãy tính chu vi của hình chữ nhật khi tăng mỗi kích thước  cm

Bài 4. Nhà bạn An ở vị trí A, nhà bạn Bình ở vị trí B cách nhau 1200 m. Trường học ở vị trí C, cách nhà bạn An 500 m và AB vuông góc với AC. An đi bộ đến trường với vận tốc 4km/h, Bình đi xe đạp đến trường với vận tốc 12 km/h. Lúc 6 giờ 30 phút, cả hai cùng xuất phát từ nhà đến trường. Hỏi bạn nào đến trường trước?

Bài 5 : Cuối học kì I năm học 2018-2019 lớp 9A có  \(\frac{4}{15}\) là học sinh giỏi , \(\frac{1}{3}\) là số học sinh khá,  còn lại 18 em học sinh trung bình . Hỏi cuối học kì I lớp 9A có bao nhiêu học sinh ?

Bài 6 :Một nông trại có tổng số gà và vịt là 600 con, sau khi bán đi 33 con gà và 7 con vịt thì số vịt còn lại bằng 40 % số gà còn lại. Hỏi sau khi bán, nông trại còn lại bao nhiêu con gà , con vịt ?

Bài 7 : Một chiếc bánh ống quế đựng kim Ý có dạng một hình nón có kích thước như hình vẽ: R = 3cm, h = 10 cm. Cho biết 1 cm2 bánh quế có khối lượng 0,12 gam. Tính khối lượng bánh ống quế khi học sinh ăn một cây kem (cho \(\Pi \approx 3,14\))

Bài 8. Cho tam giác ABC vuông tại A. Trên AC lấy một điểm D và vẽ đường tròn tâm O đường kính DC. Kẻ BD cắt đường tròn tâm O tại E.

a) Chứng minh rằng: tứ giác ABCE nội tiếp đường tròn. Xác định tâm và bán kính của đường tròn này.

b) Tia AE cắt (O) tại F. Chứng minh rằng: CA là tia phân giác của góc BCF.

c) Đường tròn (O) cắt BC tại M (M khác C). AB cắt CE tại N. Chứng minh rằng N, D, M thẳng hàng.

---(Để xem tiếp nội dung của đề thi số 5 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

Trên đây là một phần trích đoạn nội dung Bộ 5 đề thi thử vào lớp 10 môn Toán năm 2022-2023 có đáp án Trường THCS Lê Văn Tám. Để xem toàn bộ nội dung các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Mời các em tham khảo tài liệu có liên quan:

• Bộ 5 đề thi thử vào lớp 10 môn Toán năm 2022-2023 có đáp án Trường THCS Tô Hoàng
• Bộ 5 đề thi thử vào lớp 10 môn Toán năm 2022-2023 có đáp án Trường THCS Tân Lập

Hy vọng bộ đề thi này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong kì thi sắp tới.