Bộ 5 đề thi thử vào lớp 10 môn Toán năm 2022-2023 có đáp án Trường THCS Ngô Quyền

TRƯỜNG THCS NGÔ QUYỀN

ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN NĂM HỌC 2022 – 2023 Thời gian: 120 phút

Câu 1. (1,5 điểm)

 Cho (P) : \(y=-\frac{{{x}^{2}}}{2}\) và (d) : y = x – 4

a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.

b) Tìm tọa độ giao điểm của (P) và (d) bằng phép toán.

Câu 2. (1 điểm)

Cho phương trình: \(2{{x}^{2}}-13x-6=0\). Không giải phương trình, hãy tính giá trị của biểu thức A = (x₁ - x₂)² – 4x₁x₂ 

Câu 3. (1 điểm)

Gia đình ông Ba là hộ kinh doanh nhà hàng tại một thành phố lớn, nhưng do dịch bệnh covid nên 2 năm nay phần kinh doanh gần như không đáp ứng nhu cầu cuộc sống. Tháng 3 vừa qua ông trở về quê tại Long An dự định làm thêm trang trại. Ông Ba định cải tạo một mảnh vườn hình chữ nhật có chiều dài bằng 2,5 lần chiều rộng. Ông tính rằng nếu đào một cái hồ có mặt hồ là hình chữ nhật thì chiếm mất 3% diện tích mảnh vườn, còn nếu giảm chiều dài 5m và tăng chiều rộng 2m thì mặt hồ là hình vuông và diện tích mặt hồ giảm được 20m². Hỏi các cạnh vườn nhà ông Ba dài bao nhiêu mét?

Câu 4. (1 điểm)

Một lốc sữa có 4 hộp sữa, một thùng sữa có 12 lốc. Bạn An mang đủ tiền để mua 1 thùng sữa, nhưng đến nơi thì cửa hàng có chương trình khuyến mãi giảm giá 25% trên giá một hộp sữa. Biết rằng với số tiền mang theo thì vừa đủ (không thừa, không thiếu) để An mua thêm được một số hộp sữa nữa so với dự định. Hãy tính số hộp sữa An đã mua?

Câu 5. (1 điểm)

Một viên gạch trang trí nội thất có hoạ tiết như hình vẽ với hai màu tô đen và không tô đen. Em hãy tính diện tích phần không tô đen với các kích thước trên hình vẽ và lấy \(\pi \approx 3,14\) 

Câu 6. (0,75 điểm)

Một ô tô có bình xăng chứa b (lít) xăng. Gọi y là số lít xăng còn lại trong bình xăng  khi ô tô đã đi quãng đường x (km). y là hàm số bậc nhất có biến số là x được cho bởi công thức  y = ax + b (a là lượng xăng tiêu hao khi ô tô đi được 1 km và a < 0)  thỏa bảng giá trị sau.

x (km)	60	180
y (lít)	27	21

a) Tìm các hệ số a và b của hàm số bậc nhất nói trên.

b) Xe ô tô có cần đổ thêm xăng vào bình xăng hay không khi chạy hết quãng đường 700 (km) , nếu cần đổ thêm xăng thì phải đổ thêm mấy lít xăng ?

Câu 7. (0,75 điểm)

Một đống cát có dạng hình nón có chu vi đáy là \(8\pi \)m, biết độ cao của đống cát là 1,7m

a) Tính thể tích của đống cát (Lấy \(\pi =3,14\) và kết quả làm tròn đến 2 chữ số thập phân)

b) Người ta dùng xe cải tiến để chở đống cát đó đi (biết thùng chở của xe cải tiến có dạng là một hình hộp chữ nhật có kích thước rộng 1m dài 1,2m cao 50cm, và mỗi lần chở người ta chỉ gạt tới miệng xe để cát không bị rơi ra ngoài). Hỏi phải chở bao nhiêu xe cải tiến thì hết đống cát ?

Câu 8. (3 điểm)

Cho tam giác ABC (AB

a/ Chứng minh : Tứ giác AQKE nội tiếp và \(\widehat{KQE}=\widehat{BCE}\)

b/ Tia KD cắt  AC tại N. Chứng minh: Tứ giác DECN nội tiếp và EN.QK = ND.EQ.

c/ Đường thẳng QE cắt BC và AB lần lượt tại I và F. Chứng minh: \(\frac{{{S}_{END}}}{{{S}_{EQK}}}=\frac{EI}{EF}\).

ĐÁP ÁN

Câu 1:

Bảng giá trị đúng;  Vẽ đúng.

Tìm mỗi tọa độ đúng

Tọa độ giao điểm là ( -4; -8) và (2; -2)

Câu 2:

Chứng tỏ phương trình luôn có nghiệm

Tính tổng và tích đúng

S = 13/2  và P = -3

A = (x₁  - x₂)² – 4x₁x₂  = S² -8P  

A = 265/4                        

---(Để xem tiếp nội dung của đề thi số 1 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS NGÔ QUYỀN- ĐỀ 02

Bài 1. (1,5đ) Cho hàm số y = \(-{{x}^{2}}\) có đồ thị là (P) và đường thẳng (D): \(y\text{ }=\text{ }x\text{ }-\text{ 2}\)

a)  Vẽ đồ thị của hai hàm số trên cùng một hệ trục tọa độ

b)  Tìm tọa độ giao điểm của (P) và (D) bằng phép toán

Bài 2. (1,5đ) Cho phương trình \(2{{x}^{2}}-8x-5=0\) không giải phương trình.

Tính giá trị biểu thức \(D=\frac{5{{x}_{1}}-{{x}_{2}}}{{{x}_{1}}}-\frac{{{x}_{1}}-3{{x}_{2}}}{{{x}_{2}}}\)

Bài 3. (1đ) Một quyển tập giá 4000 đồng, một hộp bút giá 30000 đồng. Bạn An cần mua một số quyển tập và một hộp bút.

a)  Gọi x là số quyển tập An mua và y là số tiền phải trả (bao gồm tiền mua tập và một hộp bút).  Viết công thức biểu diễn y theo x.

b)  Nếu bạn An có 200000 đồng để mua tập và một hộp bút thì tối đa bạn An mua được bao nhiêu quyển tập

Bài 4. (1đ) Một trường THCS tổ chức cho 250 giáo viên và học sinh tham quan biết rằng giá vé vào cổng của giáo viên là 80000 đồng và học sinh là 60000 đồng.Nơi tham quan giảm giá vé cho trường học là 5% cho mổi vé nên nhà trường chi trả là 14535000 đồng .Hỏi có bao nhiêu giáo viên và học sinh tham gia ?

Bài 5. (1đ) Một cửa hàng khuyến mãi một sản phẩm bánh kem mua 4 tặng 1. Giá bán 1 bánh là 12 000 đồng. Lan muốn mua 11 bánh, Mai muốn mua 14 bánh. Mai bàn với Lan mua chung sẽ ít tốn tiền hơn từng người mua. Lan hỏi Mai mua chung sẽ đỡ tốn hơn bao nhiêu tiền và mỗi người sẽ chi trả thế nào. Em hãy trả lời giúp Mai hai câu hỏi đó?

Bài 6. (1đ) Các ống hút nhựa thường khó phân hủy và gây hại cho môi trường. Mỗi ngày có 60 triệu ống hút thải ra môi trường gây hậu quả nghiêm trọng. Ngày nay người ta chủ động sản xuất các loại ống hút dễ phân hủy. Tại tỉnh Đồng Tháp có cơ sở chuyên sản xuất ống hút “thân thiện với môi trường” xuất khẩu ra thị trường thế giới và được nhiều nước ưa chuộng. Ống hút được làm từ bột gạo, các màu chiết xuất từ củ dền, lá dứa, bông sen, bông điên điển,…Một ống hút hình trụ, đường kính 12mm, bề dày ống 2mm, chiều dài ống 180mm. Em hãy tính xem để sản xuất mỗi ống thì thể tích bột gạo được sử dụng là bao nhiêu (Biết p  ≈3,14)

Bài 7. (1đ)  Lớp 9A có 30 học sinh ,mổi bạn dự định đóng mổi tháng là 70000 đồng để mua quà tăng các trẻ em ở “Mái ấm tinh thương A” và sau 3 tháng đủ tiến để tặng mổi em ở mái ấm là 3 gói quà (giá trị mổi gói quà là như nhau).Khi các học sinh đã đóng đủ thì mái ấm đã nhận chăm sóc thêm 9 em và giá tiến mổi gói quà tăng thêm 5% nên chỉ tặng được mổi em là 2 gói quà.Hỏi lúc đầu có bao nhiêu em ổ mái ấm được tặng quà ?

Bài 8. (2đ) Từ điểm A ở ngoài đường tròn (O;R) vẽ hai tiếp tuyến AB;AC đến (O) (B;C là tiếp đểm).Vẽ đường kính BE của (O);đường thẳng AE cắt (O) tại D;AO cắt BC tại H

a) Chứng minh OA vuông góc BC và AH.AO = AD.AE

b) Chứng minh từ giác OHDE nội tiếp và HC là tia phân giác của góc DHE

c) Vẽ EK vuông góc BC;Gọi M và N là hình chiếu của O lên AE và EH.

    Chứng minh MK = NH

---(Để xem tiếp nội dung của đề thi số 2 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS NGÔ QUYỀN- ĐỀ 03

Câu 1 : (1,5 điểm)  Cho hàm số \(y=\frac{1}{3}{{x}^{2}}\) có đồ thị (P) và hàm số \(y=\frac{2}{3}x+1\) có đồ thị là đường thẳng (d).

a) Vẽ đồ thị của (P) và (d) trên cùng một hệ trục tọa độ Oxy.

b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.

Câu 2. (1,0 điểm)  Cho phương trình 2x² – 3x – 6 = 0 (1)  (m là tham số)

a) Chứng minh phương trình (1) luôn có hai nghiệm phân biệt.

b) Gọi x₁; x₂ là hai nghiệm của phương trình (1).

 Không giải phương trình, hãy tính giá trị của biểu thức: \(A=\frac{x_{1}^{2}}{x_{2}^{2}}+\frac{x_{2}^{2}}{x_{1}^{2}}\).

Câu 3. (1,0 điểm)  Cô Lan chi 116 000 000 (đồng) để nhập 1600 bao gạo và bao ngô. Mỗi bao gạo nặng 10 (kg) và được cô Lan bán ra với giá 120 000 (đồng), mỗi bao ngô nặng 15 (kg) và được cô Lan bán ra với giá 90 000 (đồng). Do thời tiết ẩm ướt, nên 20% số bao gạo và 15% số bao ngô bị hỏng không thể bán. Vì thế, tổng khối lượng gạo và ngô có thể bán lúc này là 15650 (kg).

a) Tính số bao gạo và số bao ngô cô Lan nhập về.

b) Hỏi sau khi bán hết số gạo và ngô không bị hỏng, cô Lan lời hay lỗ bao nhiêu tiền?

Câu 4. (1,0 điểm)  Galilei là người phát hiện ra quãng đường chuyển động của vật rơi tự do tỉ lệ thuận với bình phương của thời gian chuyển động. Quan hệ giữa quãng đường chuyển động y (mét) và thời gian chuyển động x (giây) được biểu diễn bởi công thức y = 4,9x². Người ta thả một vật nặng từ độ cao 55 (m).

a/ Hãy cho biết sau 2 (giây) thì vật nặng cách mặt đất bao nhiêu mét?

b/ Khi vật nặng cách mặt đất 10,9 (m) thì nó đã rơi bao nhiêu giây?

Câu 5. (1,0 điểm)  Ông An gửi ngân hàng 2 000 000 000 (đồng) với lãi suất là 6,5%/năm.
 a/ Sau 2 năm, tổng số tiền vốn và lãi ông An nhận được là bao nhiêu?
 b/ Ông An dùng số tiền đã nhận (ở câu a) để đầu tư kinh doanh. Biết sau một thời gian đầu tư, số tiền ông An nhận được cả vốn lẫn lãi là 2 608 717 500 (đồng). Hỏi lợi nhuận ông An nhận được trong đợt đầu tư kinh doanh vừa rồi là bao nhiêu phần trăm?

Câu 6. (1,0 điểm)  Một chiếc ly với phần bầu ly có dạng hình nón (như hình vẽ). Sau khi rót vào ly 60 (ml) nước thì chiều cao của lượng nước trong ly bằng \(\frac{2}{3}\) chiều cao bầu ly (\(BA=\frac{2}{3}CA\)). Công thức thể tích hình nón là V_nón = \(\frac{1}{3}\pi {{r}^{2}}h\) (r là bán kính đường tròn đáy, h là chiều cao hình nón).

a/ Tính tỉ lệ thể tích của phần nước đổ vào và thể tích bầu ly.

b/ Biếu chiều cao thân ly là HA = 5 (cm) và bánh kính miệng ly là CD = 4 (cm). Tính chiều cao của chiếc ly (đoạn CH) (kết quả làm tròn đến hàng đơn vị).

Câu 7. (1,0 điểm)  Theo âm lịch thì do một chu kỳ quay của Mặt Trăng quanh Trái Đất là khoảng 29,53 ngày nên một năm âm lịch chỉ có khoảng 354 ngày (làm tròn). Do vậy, cứ sau một vài năm âm lịch thì người ta phải bổ sung một tháng (tháng nhuận) để đảm bảo năm âm lịch tương đối phù hợp với chu kỳ của thời tiết, là yếu tố phụ thuộc vào chu kỳ quay của Trái Đất xung quanh Mặt Trời.

Cách tính năm nhuận âm lịch như sau: Lấy số năm chia cho 19, nếu số dư là một trong các số: 0; 3; 6; 9 ; 11; 14; 17 thì năm âm lịch đó có tháng nhuận.
Ví dụ: 2017 là năm nhuận âm lịch vì 2017 chia cho 19 dư 3.

2015 không phải năm nhuận âm lịch vì 2015 chia cho 19 dư 1

a) Em hãy sử dụng quy tắc trên để xác định năm 1995 và 2030 có phải năm nhuận âm lịch hay không?

b) Năm nhuận dương lịch là năm chia hết cho 4. Ngoài ra, những năm chia hết cho 100 chỉ được coi là năm nhuận dương lịch nếu chúng cũng chia hết cho 400.

Ví dụ: 1600 là năm nhuận dương lịch vì 1600 chia hết cho 400

1700 không phải năm nhuận dương lịch vì 1700  không chia hết cho 400

Hỏi từ năm 1895 đến năm 1930, năm nào vừa là năm nhuận âm lịch vừa là năm nhuận dương lịch?

Câu 8. (2,5 điểm)   Cho tam giác ABC nhọn (AB < AC) nội tiếp ( T ) có tâm O , bán kính R , BC = R  . Tiếp tuyến tại B,C của (T) cắt nhau tại P , cát tuyến PA cắt ( T ) tại D ( khác A ) . Đường thẳng OP cắt BC tại H .

a/ Chứng minh : Tam giác PBC đều . Tính PA. PD theo R?

b/ AH cắt ( T ) tại E ( khác A ) . Chứng minh : HA.HE = HO.HP và PD = PE

c/ Trên AB lấy điểm I , thỏa AI =AC , trên AC lấy điểm J thỏa AJ = AB .Đường thẳng vuông góc với AB tại I và đường thẳng vuông góc với AC tại J cắt nhau ở K . Chứng minh : IJ = BC và  AK ⊥ BC . Tính PK theo R?

---(Để xem tiếp nội dung của đề thi số 3 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS NGÔ QUYỀN- ĐỀ 04

Bài 1:  (1.5 điểm). Cho \({{({P}): y=x^{2}}}\) và \({{({d}): y=-x+2}}\)

a)  Vẽ đồ thị \(\left( P \right)\) và \(\left( d \right)\) trên cùng hệ trục tọa độ;

b)  Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép toán.

Bài 2:  (1.0 điểm) Cho phương trình \({{-x^{2}-2 x+5=0}}\)       (1).

a)  Chứng minh phương trình (1) luôn có hai nghiệm trái dấu.

b) Tìm giá trị của biểu thức \({{A=\frac{x_{1}}{x_{2}-1}-\frac{x_{2}}{1-x_{1}}+2022}}\).

Bài 3: (0.75 điểm) Một người mua hai loại hàng và phải trả tổng cộng 2,17 triệu đồng, kể cả thuế giá trị gia tăng (VAT) với mức \({{10 \%}}\) đối với loại hàng loạt hàng thứ nhất và \({{8 \%}}\) đối với loại hàng thứ hai. Nếu thuế VAT là \({{9 \%}}\) đối với cả hai loại hàng thì người đó phải trả tổng cộng 2,18 triệu đồng. Hỏi nếu không kể thuế VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại hàng?

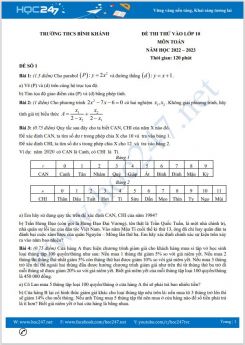
Bài 4:  (0.75 điểm) Để tìm Hàng CHI của một năm ta dùng công thức sau rồi đối chiếu kết quả với bảng sau:

Để tìm Hàng CAN của một năm ta dùng công thức sau rồi đối chiếu kết quả với bảng sau:

Hàng CAN = Chữ số tận cùng của năm dương lịch ${{-3}}$

(Nếu chữ số tận cùng của năm đang xét nhỏ hơn 3 thì ta sẽ cộng thêm 10)

 

Hàng CAN	Giáp	Âtt	Bính	Đinh	Mậu	Kỷ	Canh	Tân	Nhâm	Quý
Mã số	1	2	3	4	5	6	7	8	9	\({{10(0)}}\)

 

Bài 5:  (1.0 điểm) Bác Bình An vay ở một ngân hàng 500 triệu đồng để sản xuất trong thời hạn 1 năm. Lẽ ra đúng 1 năm sau bác phải trả cả tiền vốn lẫn tiền lãi, song bác đã được ngân hàng cho kéo dài thời hạn thêm 1 năm nữa, số tiền lãi của năm đầu được gộp vào với tiền vốn để tính lãi năm sau và lãi suất vẫn như cũ. Hết 2 năm bác Bình An phải trả tất cả 605 triệu đồng. Hỏi lãi suất cho vay của ngân hàng đó là bao nhiêu phần trăm trong 1 năm?

Bài 6:  (1.0 điểm) Sóng cực ngắn có tần số \({{30-30000 {MHz}}}\). Năng lượng rất lớn, không bị tầng điện ly hấp thụ, truyền đi rất xa \({{(>2200) {km}}}\) theo đường thẳng. Dùng trong thông tin liên lạc vũ trụ, ra đa và truyền hình. Tại một thời điểm có hai vệ tinh đang ở hai vị trí \({{A}}\) và \({{B}}\) cùng cách mặt đất \({{230 {~km}}}\), một tín hiệu (truyền bằng sóng cực ngắn) được truyền đi từ vệ tinh \({{A}}\) truyền đến vệ tinh \({{B}}\) theo phương \({{A B}}\). Hỏi vệ tinh \({{B}}\) có nhận được tín hiệu đó không? Biết khoảng cách giữa \({{A}}\) và \({{B}}\) theo đường thẳng là \({{2200 {km}}}\) và bán kính Trái Đất là \({{6400 {~km}}}\).

Bài 7:  (1.0 điểm) Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao trong bằng 3 lần đường kính trong của đáy; một viên bi hình cầu và một khối nón đều bằng thủy tinh. Biết viên bi và khối nón đều có đường kính bằng đường kính trong của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu.

Bài 8:  (3.0 điểm) Cho đường tròn tâm \({{O}}\) đường kính \({{A B}}\). Trên đường tròn \({{(O)}}\) lấy điểm \({{C}}\) không trùng \({{B}}\) sao cho \({{A C>B C}}\). Các tiếp tuyến của đường tròn \({{(O)}}\) tại \({{A}}\) và tại \({{C}}\) cắt nhau tại \({{D}}\). Gọi \({{H}}\) là hình chiếu vuông góc của \({{C}}\) trên \({{A B, E}}\) là giao điểm của hai đường thẳng \({{O D}}\) và \({{A C}}\).

a) Chứng minh \({{O E C H}}\) là tứ giác nội tiếp.

b) Gọi \({{F}}\) là giao điểm của hai đường thẳng \({{C D}}\) và \({{A B}}\). Chứng minh \({{2 \cdot \widehat{B C F}+\widehat{C F B}=90\circ}}\).

c) Gọi \({{M}}\) là giao điểm của hai đường thẳng \({{B D}}\) và \({{C H}}\); gọi \({{T}}\) là hình chiếu vuông góc của \({{O}}\) lên \({{B C}}\). Chứng minh ba điểm \({{E, M, T}}\) thẳng hàng.

---(Để xem tiếp nội dung của đề thi số 4 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS NGÔ QUYỀN- ĐỀ 05

Câu 1:  (1.5 điểm). Cho \(\left( P \right)\,\,y=-{{x}^{2}}\) và \(\left( d \right)\,\,y=x-6\)

a) Vẽ đồ thị \(\left( P \right)\) và \(\left( d \right)\) trên cùng hệ trục tọa độ.

b) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép tính.

Câu 2:  (1.0 điểm) Gọi \({{x}_{1}},\,{{x}_{2}}\) là các nghiệm của phương trình: \({{x}^{2}}-x-12=0\). Không giải phương trình hãy tính giá trị của biểu thức \(A=\frac{{{x}_{1}}+1}{{{x}_{2}}}+\frac{{{x}_{2}}+1}{{{x}_{1}}}\).

Câu 3:  (0.75 điểm) Tốc độ của một chiếc ca nô và độ dài đường sóng nước để lại sau đuôi của nó được cho bởi công thức \(v=5\sqrt{d}\). Trong đó \(d\,(\text{m})\) là độ dài đường sóng nước để lại sau đuôi ca nô, v là vận tốc ca nô (m/giây).

a) Tính vận tốc ca nô biết độ dài đường sóng nước để lại sau đuôi ca nô dài \(7+4\sqrt{3}\,(\text{m})\).

b) Khi ca nô chạy với vận tốc 54 km/giờ thì đường sóng nước để lại sau đuôi ca nô dài bao nhiêu mét?

Câu 4:  (0.75 điểm) Trong kết quả xét nghiệm lượng đường trong máu có bệnh viện tính theo đơn vị là \(\text{mg/dl}\) nhưng cũng có bệnh viện tính theo đơn vị là \(\text{mmol/l}\). Công thức chuyển đổi là \(\text{1}\,\text{mmol/l}\,\text{=}\,\frac{1}{18}\,\text{mg/dl}\). Hai bạn Châu và Lâm nhịn ăn sáng sau khi thử đường huyết tại nhà có chỉ số đường huyết lần lượt là \(\text{110}\,\text{mg/dl}\) và \(\text{90}\,\text{mg/dl}\). Căn cứ vào bảng sau, em hãy cho biết tình trạng

sức khỏe của hai bạn Châu và Lâm:

Tên xét nghiệm	Hạ đường huyết	Đường huyết bình thường	Giai đoạn tiền tiểu đường	Chuẩn đoán bệnh tiểu đường
Đường huyết lúc đói \(x\,(\text{mmol/l)}\)	x<4.0 \((\text{mmol/l)}\)	\(4.0\le x\le 5.6\) \((\text{mmol/l)}\)	\(5.6 < x < 7.0\) \((\text{mmol/l)}\)	\(x\ge 7.0\) \((\text{mmol/l)}\)

Câu 5:  (1.0 điểm) Một chiếc vòng nữ trang được làm từ vàng và bạc với thể tích là \(10\text{ c}{{\text{m}}^{3}}\) và cân nặng

\(171\text{ g}\). Biết vàng có khối lượng riêng là \(19,3\text{ g/c}{{\text{m}}^{3}}\) còn bạc có khối lượng riêng là \(10,5\text{ g/c}{{\text{m}}^{3}}\). Hỏi thể tích của vàng và bạc được sử dụng để làm chiếc vòng? Biết công thức tính khối lượng là m=D.V, trong đó m là khối lượng, D là khối lượng riêng và V là thể tích.

Câu 6:  (1.0 điểm) Một bình chứa nước hình hộp chữ nhật có diện tích đáy là \(20\text{ d}{{\text{m}}^{2}}\) và chiều cao \(3\text{ dm}\). Người ta rót hết nước trong bình ra những chai nhỏ mỗi chai có thể tích \(0,35\text{ d}{{\text{m}}^{3}}\) được tất cả 72 chai. Hỏi lượng nước có trong bình chiếm bao nhiêu phần trăm thể tích bình?

Câu 7: (1.0 điểm) Trong tháng 12 năm 2021 khi Thành phố Hồ Chí Minh cho các học sinh lớp 9 trở lại trường học trực tiếp sau những tháng ngày học trực tuyến, tôi đã về lại trường cũ để lãnh những phần thưởng mà tôi đã gặt hái được trong năm học vừa qua do dịch bệnh nên không đến nhận phần thưởng được. Vui mừng khi tôi gặp lại thầy chủ nhiệm lớp 9. Qua chuyện thầy cho tôi biết lớp tôi sĩ số cuối năm giảm \(\frac{1}{21}\) so với đầu năm, toàn bộ lớp đều tham gia xét tuyển sinh lớp 10 và kết quả có 34 học sinh đã đậu vào lớp 10 công lập đạt tỉ lệ \(85\,%\). Các bạn hãy tính sĩ số đầu năm của lớp tôi là bao nhiêu?

Câu 8: (3.0 điểm) Cho tam giác nhọn \(ABC\,\left( AB

a)  Chứng minh: \(\widehat{AFE}=\widehat{ADE}\) và tứ giác BCEF nội tiếp.

b)  Tia EF cắt tia CB tại M, đoạn thẳng AM cắt đường tròn \(\left( O \right)\) tại N (khác A). Chứng minh AF.AB=AE.AC và MN.MA=MF.ME.

c)  Tia ND cắt đường tròn \(\left( O \right)\) tại I. Chứng minh \(OI\bot EF\).

---(Để xem tiếp nội dung của đề thi số 5 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

Trên đây là một phần trích đoạn nội dung Bộ 5 đề thi thử vào lớp 10 môn Toán năm 2022-2023 có đáp án Trường THCS Ngô Quyền. Để xem toàn bộ nội dung các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Hy vọng bộ đề thi này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong kì thi sắp tới.