Xin giß╗øi thiß╗ću ─æß║┐n c├Īc em nß╗Öi dung t├Āi liß╗ću Bß╗Ö 5 ─æß╗ü thi thß╗Ł v├Āo lß╗øp 10 m├┤n To├Īn n─ām 2022-2023 c├│ ─æ├Īp ├Īn TrŲ░ß╗Øng THCS T├ón Lß║Łp gi├║p c├Īc em vß╗½a hß╗ć thß╗æng to├Ān diß╗ćn kiß║┐n thß╗®c vß╗½a luyß╗ćn tß║Łp c├Īc dß║Īng b├Āi tß║Łp ─æß╗ā chuß║®n bß╗ŗ thß║Łt tß╗æt cho k├¼ thi tuyß╗ān sinh v├Āo lß╗øp 10 sß║»p tß╗øi. HOC247 mß╗Øi qu├Į thß║¦y, c├┤ v├Ā c├Īc em hß╗Źc sinh theo d├Ąi nß╗Öi dung chi tiß║┐t t├Āi liß╗ću b├¬n dŲ░ß╗øi!
|
TRŲ»ß╗£NG THCS T├ö HO├ĆNG |
─Éß╗Ć THI THß╗¼ V├ĆO Lß╗ÜP 10 M├öN TO├üN N─éM Hß╗īC 2022 ŌĆō 2023 Thß╗Øi gian: 120 ph├║t |
─Éß╗Ć Sß╗É 1
C├óu 1.(1,5 ─æiß╗ām).
a) Vß║Į ─æß╗ō thß╗ŗ h├Ām sß╗æ \(\left( P \right):y=-{{x}^{2}}\) v├Ā ─æŲ░ß╗Øng thß║│ng \(\left( d \right):y=-4x+3\) tr├¬n c├╣ng mß╗Öt mß║Ęt phß║│ng tß╗Źa ─æß╗Ö.
b) T├¼m tß╗Źa ─æß╗Ö giao ─æiß╗ām cß╗¦a \(\left( P \right)\) v├Ā \(\left( d \right)\) bß║▒ng ph├®p to├Īn.
C├óu 2. (1 ─æiß╗ām). Cho phŲ░ŲĪng tr├¼nh: \(3{{x}^{2}}+2x-9=0\) c├│ hai nghiß╗ćm l├Ā \({{x}_{1}},{{x}_{2}}.\) Kh├┤ng giß║Żi phŲ░ŲĪng tr├¼nh tr├¬n, h├Ży t├Łnh gi├Ī trß╗ŗ cß╗¦a biß╗āu thß╗®c \(A=\left( 3{{x}_{1}}2{{x}_{2}} \right)\left( 3{{x}_{2}}2{{x}_{1}} \right)\)
C├óu 3.(1 ─æiß╗ām). Ng├Āy \(28/09/2018\), sau trß║Łn ─æß╗Öng ─æß║źt \(7,5\) ─æß╗Ö Richter, cŲĪn s├│ng thß║¦n (tiß║┐ng Anh l├Ā Tsunami) cao hŲĪn \(6\text{ m}\) ─æ├Ż tr├Ān v├Āo ─æß║Żo Sulawesi cß╗¦a In ─æ├┤ n├¬ xi a, t├Ān ph├Ī th├Ānh phß╗æ Palu, g├óy thiß╗ćt hß║Īi v├┤ c├╣ng to lß╗øn. Tß╗æc ─æß╗Ö cß╗¦a cŲĪn s├│ng thß║¦n v├Ā chiß╗üu s├óu cß╗¦a ─æß║Īi dŲ░ŲĪng, nŲĪi bß║»t ─æß║¦u cß╗¦a s├│ng thß║¦n, li├¬n hß╗ć bß╗¤i c├┤ng thß╗®c \(v=\sqrt{dg}\). Trong ─æ├│, \(g=9,81\text{ m/}{{\text{s}}^{\text{2}}}\), d l├Ā chiß╗üu s├óu cß╗¦a ─æß║Īi dŲ░ŲĪng t├Łnh bß║▒ng m, v l├Ā vß║Łn tß╗æc cß╗¦a s├│ng thß║¦n t├Łnh bß║▒ng m/s
a) Biß║┐t ─æß╗Ö s├óu trung b├¼nh tß║Īi Th├Īi B├¼nh DŲ░ŲĪng l├Ā \(4000\,\text{m}\), h├Ży t├Łnh tß╗æc ─æß╗Ö trung b├¼nh cß╗¦a c├Īc con s├│ng thß║¦n xuß║źt ph├Īt tß╗½ ─æ├Īy cß╗¦a Th├Īi B├¼nh DŲ░ŲĪng.
b) Theo t├Łnh to├Īn cß╗¦a c├Īc nh├Ā khoa hß╗Źc ─æß╗ŗa chß║źt, vß║Łn tß╗æc cß╗¦a ─æß╗Żt s├│ng thß║¦n ng├Āy \(28/09/2018\) c├│ vß║Łn tß╗æc l├Ā \(800\text{ km/h}\), h├Ży t├Łnh chiß╗üu s├óu cß╗¦a ─æß║Īi dŲ░ŲĪng, nŲĪi t├óm chß║źn ─æß╗Öng ─æß║źt g├óy ra s├│ng thß║¦n l├Ā bao nhi├¬u m?
C├óu 4.(1,0 ─æiß╗ām). Vß╗øi sß╗▒ ph├Īt triß╗ān cß╗¦a khoa hß╗Źc kß╗╣ thuß║Łt hiß╗ćn nay, nguß╗Øi ta tß║Īo ra nhiß╗üu mß║½u xe l─ān ─æß║╣p v├Ā tiß╗ćn dß╗źng cho ngŲ░ß╗Øi khuyß║┐t tß║Łt. C├┤ng ty A ─æ├Ż sß║Żn xuß║źt ra nhß╗»ng chiß║┐c xe l─ān cho nguß╗Øi khuyß║┐t tß║Łt vß╗øi sß╗æ vß╗æn ban ─æß║¦u l├Ā 500 triß╗ću ─æß╗ōng. Chi ph├Ł ─æß╗ā sß║Żn xuß║źt ra mß╗Öt chiß║┐c xe l─ān l├Ā 2.500.000 ─æß╗ōng. Gi├Ī b├Īn ra mß╗Śi chiß║┐c l├Ā 3.000.000 ─æß╗ōng.
a) Viß║┐t h├Ām sß╗æ biß╗āu diß╗ģn tß╗Ģng sß╗æ tiß╗ün ─æ├Ż ─æß║¦u tŲ░ ─æß║┐n khi sß║Żn xuß║źt ra ─æŲ░ß╗Żc x chiß║┐c xe l─ān (gß╗ōm vß╗æn ban ─æß║¦u v├Ā chi ph├Ł sß║Żn xuß║źt) v├Ā h├Ām sß╗æ biß╗āu diß╗ģn sß╗æ tiß╗ün thu ─æŲ░ß╗Żc khi b├Īn ra x chiß║┐c xe l─ān.
b) C├┤ng ty A phß║Żi b├Īn bao nhi├¬u chiß║┐c xe mß╗øi c├│ thß╗ā thu hß╗ōi ─æŲ░ß╗Żc vß╗æn ban ─æß║¦u?
C├óu 5.(1 ─æiß╗ām). ─Éß╗ā gi├║p c├Īc bß║Īn trß║╗ ŌĆ£khß╗¤i nghiß╗ćpŌĆØ, ng├ón h├Āng cho vay vß╗æn Ų░u ─æ├Żi vß╗øi l├Żi suß║źt 5% /n─ām. Mß╗Öt nh├│m bß║Īn trß║╗ vay 100 triß╗ću ─æß╗ōng l├Ām vß╗æn kinh doanh h├Āng tiß╗āu thß╗¦ c├┤ng mß╗╣ nghß╗ć.
a) Hß╗Åi sau mß╗Öt n─ām c├Īc bß║Īn trß║╗ phß║Żi trß║Ż cho ng├ón h├Āng cß║Ż vß╗æn lß║½n l├Żi l├Ā bao nhi├¬u?
b) C├Īc bß║Īn trß║╗ kinh doanh hai ─æß╗Żt trong n─ām, ─æß╗Żt 1 sau khi trß╗½ c├Īc chi ph├Ł thß║źy l├Żi ─æŲ░ß╗Żc 18% so vß╗øi vß╗æn bß╗Å ra n├¬n dß╗ōn cß║Ż vß╗æn lß║½n l├Żi ─æß╗ā kinh doanh tiß║┐p ─æß╗Żt 2, cuß╗æi ─æß╗Żt 2 trß╗½ c├Īc chi ph├Ł thß║źy l├Żi 20% so vß╗øi vß╗æn ─æß╗Żt 2 bß╗Å ra. Hß╗Åi sau 2 ─æß╗Żt kinh doanh, trß║Ż hß║┐t nß╗Ż ng├ón h├Āng, c├Īc bß║Īn trß║╗ c├▓n l├Żi ─æŲ░ß╗Żc bao nhi├¬u tiß╗ün?
C├óu 6.(1 ─æiß╗ām). Mß╗Öt bß╗ōn ─æß╗▒ng nŲ░ß╗øc c├│ dß║Īng h├¼nh hß╗Öp chß╗» nhß║Łt c├│ c├Īc k├Łch thŲ░ß╗øc cho tr├¬n h├¼nh vß║Į
a) T├Łnh diß╗ćn t├Łch bß╗ü mß║Ęt cß╗¦a bß╗ōn (kh├┤ng t├Łnh nß║»p)?
b) Mß╗Öt v├▓i bŲĪm vß╗øi c├┤ng suß║źt 120 l├Łt/ph├║t ─æß╗ā bŲĪm mß╗Öt lŲ░ß╗Żng nŲ░ß╗øc v├Āo bß╗ōn l├¬n ─æß╗Ö cao c├Īch nß║»p bß╗ōn l├Ā \(1,5\text{ m}\) th├¼ phß║Żi mß║źt bao l├óu? (bß╗ōn kh├┤ng chß╗®a nŲ░ß╗øc)
.JPG)
C├óu 7.(1 ─æiß╗ām). Hai trŲ░ß╗Øng A v├Ā B c├│ 420 hß╗Źc sinh ─æß║Łu v├Āo lß╗øp 10 ─æß║Īt tß╗ē lß╗ć 84%. Ri├¬ng trŲ░ß╗Øng A tß╗ē lß╗ć ─æß║Łu 80%, ri├¬ng trŲ░ß╗Øng B tß╗ē lß╗ć ─æß║Łu 90%. T├Łnh sß╗æ hß╗Źc sinh dß╗▒ thi cß╗¦a mß╗Śi trŲ░ß╗Øng?
C├óu 8.(3 ─æiß╗ām) Cho ─æŲ░ß╗Øng tr├▓n \(\left( O;\text{ }4\text{ cm} \right)\) v├Ā ─æiß╗ām A ß╗¤ ngo├Āi \(\left( O \right)\) vß╗øi \(OA=8\text{ cm}\). Tia AO cß║»t ─æŲ░ß╗Øng tr├▓n \(\left( O \right)\) tß║Īi hai ─æiß╗ām D v├Ā E (D nß║▒m giß╗»a hai ─æiß╗ām A v├Ā O), c├Īt tuyß║┐n ACB cß║»t ─æŲ░ß╗Øng tr├▓n \(\left( O \right)\) tß║Īi hai ─æiß╗ām C v├Ā B (C nß║▒m giß╗»a hai ─æiß╗ām A v├Ā B).
a) Chß╗®ng minh \(\widehat{ACD}=\widehat{AEB}\) v├Ā AC.AB=AD.AE.
b) Gß╗Źi \(H\) l├Ā trung ─æiß╗ām cß╗¦a ─æoß║Īn thß║│ng \(OD\). Chß╗®ng minh tß╗® gi├Īc \(OHCB\) nß╗Öi tiß║┐p.
c) Tia ─æß╗æi cß╗¦a tia ph├ón gi├Īc \(\widehat{CHB}\) cß║»t ─æŲ░ß╗Øng tr├▓n \(\left( O \right)\) tß║Īi M. Chß╗®ng minh AM l├Ā tiß║┐p tuyß║┐n ─æŲ░ß╗Øng tr├▓n \(\left( O \right)\) tß║Īi M.
ĐÁP ÁN
Câu 1:
a) Vß║Į ─æß╗ō thß╗ŗ h├Ām sß╗æ \(\left( P \right):y=-{{x}^{2}}\) v├Ā ─æŲ░ß╗Øng thß║│ng \(\left( d \right):y=-4x+3\) tr├¬n c├╣ng mß╗Öt mß║Ęt phß║│ng tß╗Źa ─æß╗Ö.
BGT:
(thu nhß╗Å ─æiß╗ām tr├¬n ─æß╗ō thß╗ŗ chß╗» x, y chuyß╗ān sang in nghi├¬ng cho ─æß╗ōng bß╗Ö vs x, y trong b├Āi l├Ām ŌĆō n├¬n x├│a nß╗ün ├┤ vu├┤ng)
b) T├¼m tß╗Źa ─æß╗Ö giao ─æiß╗ām cß╗¦a \(\left( P \right)\) v├Ā \(\left( d \right)\) bß║▒ng ph├®p t├Łnh.
PhŲ░ŲĪng tr├¼nh ho├Ānh ─æß╗Ö giao ─æiß╗ām cß╗¦a \(\left( P \right)\) v├Ā \(\left( d \right): \Leftrightarrow - {x^2} + 4x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 1\\
x = 3
\end{array} \right.{\rm{ }}\)
Thay x=1 v├Āo \(y=-{{x}^{2}}\), ta ─æŲ░ß╗Żc: \(y=-{{1}^{2}}=-1\).
Thay x=3 v├Āo \(y=-{{x}^{2}}\), ta ─æŲ░ß╗Żc: \(y=-{{3}^{2}}=-9\).
Vß║Ły \(\left( 1;\,\,-1 \right)\), \(\left( 3;\,\,-9 \right)\) l├Ā hai giao ─æiß╗ām cß║¦n t├¼m
---(─Éß╗ā xem tiß║┐p nß╗Öi dung cß╗¦a ─æß╗ü thi sß╗æ 1 c├Īc em vui l├▓ng xem tß║Īi online hoß║Ęc ─æ─āng nhß║Łp v├Āo Hß╗īC247 ─æß╗ā tß║Żi vß╗ü m├Īy)---
─Éß╗Ć Sß╗É 2
─Éß╗Ć THI THß╗¼ V├ĆO Lß╗ÜP 10 M├öN TO├üN TRŲ»ß╗£NG THCS T├ö HO├ĆNG- ─Éß╗Ć 02
C├óu 1.1,5 ─æiß╗ām). Cho \(\left( P \right):y=-\frac{1}{2}{{x}^{2}}\) v├Ā ─æŲ░ß╗Øng thß║│ng \(\left( d \right):y=x-4\).
a) Vß║Į ─æß╗ō thß╗ŗ \(\left( P \right)\) v├Ā \(\left( d \right)\) tr├¬n c├╣ng hß╗ć trß╗źc tß╗Źa ─æß╗Ö.
b) T├¼m tß╗Źa ─æß╗Ö giao ─æiß╗ām cß╗¦a \(\left( P \right)\) v├Ā \(\left( d \right)\) bß║▒ng ph├®p t├Łnh.
C├óu 2. (1 ─æiß╗ām). Cho phŲ░ŲĪng tr├¼nh \({{x}^{2}}\text{ }7x\text{ }+\text{ }12\text{ }=\text{ }0\) c├│ 2 nghiß╗ćm l├Ā \({{x}_{1}},{{x}_{2}}\). Kh├┤ng giß║Żi phŲ░ŲĪng tr├¼nh, h├Ży t├Łnh gi├Ī trß╗ŗ cß╗¦a biß╗āu thß╗®c \(A={{x}_{1}}^{2}+{{x}_{2}}^{2}-{{x}_{1}}-{{x}_{2}}\)
C├óu 3. (0,75 ─æiß╗ām). Trong mß╗Öt th├Īng khoß║Żng lß╗Żi nhuß║Łn y (─æß╗ōng) cß╗¦a mß╗Öt cß╗Ła h├Āng thu ─æŲ░ß╗Żc khi b├Īn x hß╗Öp sß╗»a loß║Īi 900g ─æŲ░ß╗Żc cho bß╗¤i phŲ░ŲĪng tr├¼nh \(y\text{ }=\text{ }ax\text{ }+\text{ }b\). Biß║┐t rß║▒ng trong th├Īng 10 cß╗Ła h├Āng b├Īn ─æŲ░ß╗Żc 95 hß╗Öp sß╗»a thu lß╗Żi nhuß║Łn \(4\text{ }870\text{ }000\) ─æß╗ōng, th├Īng 11 b├Īn ─æŲ░ß╗Żc 180 hß╗Öp sß╗»a thu ─æŲ░ß╗Żc lß╗Żi nhuß║Łn \(9\text{ }120\text{ }000\) ─æß╗ōng. T├Łnh hß╗ć sß╗æ a v├Ā b?
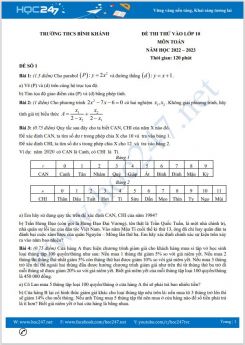
C├óu 4.(0,75 ─æiß╗ām). Theo ├óm lß╗ŗch th├¼ do mß╗Öt chu kß╗│ quay cß╗¦a Mß║Ęt Tr─āng quanh Tr├Īi ─Éß║źt l├Ā khoß║Żng 29,53 ng├Āy n├¬n mß╗Öt n─ām ├óm lß╗ŗch chß╗ē c├│ khoß║Żng 354 ng├Āy (l├Ām tr├▓n). Do vß║Ły, cß╗® sau mß╗Öt v├Āi n─ām ├óm lß╗ŗch th├¼ ngŲ░ß╗Øi ta phß║Żi bß╗Ģ sung mß╗Öt th├Īng (th├Īng nhuß║Łn) ─æß╗ā ─æß║Żm bß║Żo n─ām ├óm lß╗ŗch tŲ░ŲĪng ─æß╗æi ph├╣ hß╗Żp vß╗øi chu kß╗│ cß╗¦a thß╗Øi tiß║┐t, l├Ā yß║┐u tß╗æ phß╗ź thuß╗Öc v├Āo chu kß╗│ quay cß╗¦a Tr├Īi ─Éß║źt xung quanh Mß║Ęt Trß╗Øi. C├Īch t├Łnh n─ām nhuß║Łn ├óm lß╗ŗch nhŲ░ sau:
Lß║źy sß╗æ n─ām chia cho 19, nß║┐u sß╗æ dŲ░ l├Ā mß╗Öt trong c├Īc sß╗æ: \(0;\text{ }3;\text{ }6;\text{ }9\text{ };\text{ }11;\text{ }14;\text{ }17\) th├¼ n─ām ├óm lß╗ŗch ─æ├│ c├│ th├Īng nhuß║Łn.
V├Ł dß╗ź: 2017 l├Ā n─ām nhuß║Łn ├óm lß╗ŗch v├¼ 2017 chia cho 19 dŲ░ 3.
2015 kh├┤ng phß║Żi n─ām nhuß║Łn ├óm lß╗ŗch v├¼ 2015 chia cho 19 dŲ░ 1.
a) Em h├Ży sß╗Ł dß╗źng quy tß║»c tr├¬n ─æß╗ā x├Īc ─æß╗ŗnh n─ām 1995 v├Ā 2030 c├│ phß║Żi n─ām nhuß║Łn ├óm lß╗ŗch hay kh├┤ng?
b) N─ām nhuß║Łn dŲ░ŲĪng lß╗ŗch l├Ā n─ām chia hß║┐t cho 4. Ngo├Āi ra, Nhß╗»ng n─ām chia hß║┐t cho 100 chß╗ē ─æŲ░ß╗Żc coi l├Ā n─ām nhuß║Łn dŲ░ŲĪng lß╗ŗch nß║┐u ch├║ng c┼®ng chia hß║┐t cho 400 (v├Ł dß╗ź 1600 l├Ā n─ām nhuß║Łn dŲ░ŲĪng lß╗ŗch nhŲ░ng 1700 kh├┤ng phß║Żi n─ām nhuß║Łn dŲ░ŲĪng lß╗ŗch). Trong c├Īc n─ām tß╗½ n─ām 1895 ─æß║┐n n─ām 1930, n─ām n├Āo vß╗½a l├Ā n─ām nhuß║Łn ├óm lß╗ŗch vß╗½a l├Ā n─ām nhuß║Łn dŲ░ŲĪng lß╗ŗch.
C├óu 5.(1 ─æiß╗ām). Th├Īng 6/2021 gia ─æ├¼nh ├┤ng Hai thu nhß║Łp 15.000.000 ─æß╗ōng v├Ā chi ti├¬u 12.000.000 ─æß╗ōng. Th├Īng 7/2021 thu nhß║Łp giß║Żm 10% m├Ā chi ti├¬u lß║Īi t─āng 13%. Hß╗Åi ├┤ng Hai c├▓n ─æß╗ā d├Ānh tiß╗ün ─æŲ░ß╗Żc kh├┤ng ?
C├óu 6.(1 ─æiß╗ām). Mß╗Öt bß╗ā k├Łnh nu├┤i c├Ī c├│ dß║Īng h├¼nh hß╗Öp chß╗» nhß║Łt c├│ chiß╗üu d├Āi 100cm, chiß╗üu rß╗Öng 50cm, chiß╗üu cao 60cm. Mß╗▒c nŲ░ß╗øc trong bß╗ā cao bß║▒ng \(\frac{3}{4}\) chiß╗üu cao bß╗ā. T├Łnh thß╗ā t├Łch nŲ░ß╗øc trong bß╗ā ─æ├│ (─æß╗Ö d├Āy k├Łnh kh├┤ng ─æ├Īng kß╗ā). C├┤ng thß╗®c t├Łnh thß╗ā t├Łch nŲ░ß╗øc trong bß╗ā l├Ā V=S.h vß╗øi S l├Ā diß╗ćn t├Łch mß║Ęt ─æ├Īy bß╗ā v├Ā h l├Ā chiß╗üu cao mß╗▒c nŲ░ß╗øc trong bß╗ā.
C├óu 7.(1 ─æiß╗ām). B├Ā nß╗Öi d├Ānh dß╗źm ─æŲ░ß╗Żc mß╗Öt sß╗æ tiß╗ün ─æß╗ā thŲ░ß╗¤ng cho c├Īc ch├Īu cß╗¦a b├Ā. Nß║┐u b├Ā thŲ░ß╗¤ng cho mß╗Śi ch├Īu 140000 ─æß╗ōng th├¼ b├Ā c├▓n dŲ░ 40000 ─æß╗ōng, nß║┐u b├Ā thŲ░ß╗¤ng cho mß╗Śi ch├Īu 160000 ─æß╗ōng th├¼ b├Ā c├▓n thiß║┐u 60000 ─æß╗ōng. Hß╗Åi b├Ā nß╗Öi d├Ānh dß╗źm ─æŲ░ß╗Żc bao nhi├¬u tiß╗ün v├Ā c├│ bao nhi├¬u ch├Īu ?
C├óu 8. (3 ─æiß╗ām) Tß╗½ ─æiß╗ām A ß╗¤ ngo├Āi ─æŲ░ß╗Øng tr├▓n \(\left( O;R \right)\), vß║Į hai tiß║┐p tuyß║┐n \(AB,\text{ }AC\) v├Ā c├Īt tuyß║┐n \(AMN\) vß╗øi ─æŲ░ß╗Øng tr├▓n (B, C l├Ā c├Īc tiß║┐p ─æiß╗ām, AM < AN v├Ā tia AM nß║▒m giß╗»a hai tia AB, AO). Gß╗Źi I l├Ā h├¼nh chiß║┐u cß╗¦a O tr├¬n AN, H l├Ā giao ─æiß╗ām cß╗¦a OA v├Ā BC. Chß╗®ng minh:
a) Tß╗® gi├Īc OABI nß╗Öi tiß║┐p v├Ā x├Īc ─æß╗ŗnh t├óm cß╗¦a ─æŲ░ß╗Øng tr├▓n ngoß║Īi tiß║┐p tß╗® gi├Īc.
b) IA l├Ā tia ph├ón gi├Īc cß╗¦a \(\widehat{BIC}\)
c) ─Éiß╗ām H thuß╗Öc ─æŲ░ß╗Øng tr├▓n ngoß║Īi tiß║┐p \(\Delta OMN\)
---(─Éß╗ā xem tiß║┐p nß╗Öi dung cß╗¦a ─æß╗ü thi sß╗æ 2 c├Īc em vui l├▓ng xem tß║Īi online hoß║Ęc ─æ─āng nhß║Łp v├Āo Hß╗īC247 ─æß╗ā tß║Żi vß╗ü m├Īy)---
─Éß╗Ć Sß╗É 3
─Éß╗Ć THI THß╗¼ V├ĆO Lß╗ÜP 10 M├öN TO├üN TRŲ»ß╗£NG THCS T├ö HO├ĆNG- ─Éß╗Ć 03
B├Āi 1 . Cho h├Ām sß╗æ : (P): \(y={{x}^{2}}\) v├Ā ─æŲ░ß╗Øng thß║│ng (D) : \(y=\frac{1}{2}x+3\)
a) Vß║Į ─æß╗ō thß╗ŗ (P) v├Ā (D) tr├¬n c├╣ng mß║Ęt phß║│ng tß╗Źa ─æß╗Ö.
b) T├¼m tß╗Źa ─æß╗Ö giao ─æiß╗ām cß╗¦a (P) v├Ā (D) bß║▒ng ph├®p to├Īn.
B├Āi 2 Cho phŲ░ŲĪng tr├¼nh ß║®n x : x2 ŌĆō (2m + 1)x + m2 + m ŌĆō 2 = 0 (1)
a) Chß╗®ng minh phŲ░ŲĪng tr├¼nh (1) lu├┤n c├│ hai nghiß╗ćm ph├ón biß╗ćt x1, x2 vß╗øi mß╗Źi m.
b) T├¼m m thß╗Åa hß╗ć thß╗®c : x1(x1 ŌĆō 2x2) + x2(x2 ŌĆō 3x1) = 9
B├Āi 3 Gia ─æ├¼nh bß║Īn An mua mß╗Öt khu ─æß║źt h├¼nh chß╗» nhß║Łt ─æß╗ā cß║źt nh├Ā. Biß║┐t chiß╗üu d├Āi gß║źp 4 lß║¦n chiß╗üu rß╗Öng. Theo quy hoß║Īch, khi x├óy nh├Ā phß║Żi chß╗½a 2m (theo chiß╗üu d├Āi) ph├Ła sau ─æß╗ā l├Ām giß║┐ng trß╗Øi v├Ā 4m ph├Ła trŲ░ß╗øc (theo chiß╗üu d├Āi) ─æß╗ā trß╗ōng c├óy xanh n├¬n diß╗ćn t├Łch x├óy nh├Ā chß╗ē c├▓n 75% diß╗ćn t├Łch khu ─æß║źt. Hß╗Åi chu vi l├║c ─æß║¦u cß╗¦a khu ─æß║źt.
B├Āi 4. C├│ hai lß╗Ź ─æß╗▒ng muß╗æi vß╗øi nß╗ōng ─æß╗Ö 5% v├Ā 40%. Hß╗Åi cß║¦n phß║Żi lß║źy mß╗Śi loß║Īi bao nhi├¬u gam ─æß╗ā ─æŲ░ß╗Żc 140g nŲ░ß╗øc muß╗æi vß╗øi nß╗ōng ─æß╗Ö 30%?
B├Āi 5 Tß╗½ ─æ├Āi quan s├Īt cao 15m (t├Łnh tß╗½ mß╗▒c nŲ░ß╗øc biß╗ān), bß║Īn An c├│ thß╗ā nh├¼n thß║źy hai chiß║┐c thuyß╗ün dŲ░ß╗øi g├│c hß║Ī 400 v├Ā 100 so vß╗øi phŲ░ŲĪng ngang. H├Ży t├Łnh khoß║Żng c├Īch 2 chiß║┐c thuyß╗ün (l├Ām tr├▓n ─æß║┐n chß╗» sß╗æ h├Āng ─æŲĪn vß╗ŗ)? ─Éiß╗üu kiß╗ćn l├Į tŲ░ß╗¤ng: vß╗ŗ tr├Ł 2 chiß║┐c thuyß╗ün v├Ā vß╗ŗ tr├Ł ─æ├Āi quan s├Īt thß║│ng h├Āng.
B├Āi 6. Mß╗Öt hß╗ō bŲĪi c├│ dß║Īng l├Ā mß╗Öt l─āng trß╗ź ─æß╗®ng tß╗® gi├Īc vß╗øi ─æ├Īy l├Ā h├¼nh thang vu├┤ng (mß║Ęt b├¬n (1) cß╗¦a hß╗ō bŲĪi l├Ā 1 ─æ├Īy cß╗¦a l─āng trß╗ź) v├Ā c├Īc k├Łch thŲ░ß╗øc nhŲ░ ─æ├Ż cho (xem h├¼nh 2). Biß║┐t rß║▒ng ngŲ░ß╗Øi ta d├╣ng mß╗Öt m├Īy bŲĪm vß╗øi lŲ░u lŲ░ß╗Żng l├Ā 42 m3/ph├║t v├Ā sß║Į bŲĪm ─æß║¦y hß╗ō mß║źt 25 ph├║t. T├Łnh chiß╗üu d├Āi cß╗¦a hß╗ō.
B├Āi 7. Cho ─æŲ░ß╗Øng tr├▓n (O ; R), ─æŲ░ß╗Øng k├Łnh AB. Tr├¬n ─æŲ░ß╗Øng tr├▓n lß║źy ─æiß╗ām C sao cho BC > AC. C├Īc tiß║┐p tuyß║┐n tß║Īi A v├Ā tß║Īi C cß╗¦a (O) cß║»t nhau tß║Īi D.
a) Chß╗®ng minh tß╗® gi├Īc ADCO nß╗Öi tiß║┐p v├Ā OD // BC.
b) CD cß║»t BA tß║Īi S, vß║Į AH \(\bot\) DS ß╗¤ H. Chß╗®ng minh: DC2 = DH.DS v├Ā SD.HC = SC.CD.
c) Qua S kß║╗ ─æŲ░ß╗Øng thß║│ng (d) song song vß╗øi AD ; (d) cß║»t tia BD v├Ā tia CA lß║¦n lŲ░ß╗Żt tß║Īi M v├Ā E. Chß╗®ng minh BS l├Ā tia ph├ón gi├Īc cß╗¦a g├│c CBE v├Ā SE = 2SM.
---(─Éß╗ā xem tiß║┐p nß╗Öi dung cß╗¦a ─æß╗ü thi sß╗æ 3 c├Īc em vui l├▓ng xem tß║Īi online hoß║Ęc ─æ─āng nhß║Łp v├Āo Hß╗īC247 ─æß╗ā tß║Żi vß╗ü m├Īy)---
─Éß╗Ć Sß╗É 4
─Éß╗Ć THI THß╗¼ V├ĆO Lß╗ÜP 10 M├öN TO├üN TRŲ»ß╗£NG THCS T├ö HO├ĆNG- ─Éß╗Ć 04
B├Āi 1. Cho parabol \((P):y=-\ {{x}^{2}}\) v├Ā ─æŲ░ß╗Øng thß║│ng \((d):y=2x-3\)
a) Vß║Į (P) v├Ā (d) tr├¬n c├╣ng hß╗ć trß╗źc tß╗Źa ─æß╗Ö.
b) T├¼m tß╗Źa ─æß╗Ö giao ─æiß╗ām cß╗¦a (d) v├Ā (P) bß║▒ng ph├®p t├Łnh.
B├Āi 2. Cho phŲ░ŲĪng tr├¼nh: \(3{{x}^{2}}+6x-1=0\) c├│ hai nghiß╗ćm \({{x}_{1}}\ ;\ {{x}_{2}}\).
Kh├┤ng giß║Żi phŲ░ŲĪng tr├¼nh, h├Ży t├Łnh gi├Ī trß╗ŗ cß╗¦a biß╗āu thß╗®c: \(A={{x}_{1}}^{3}+{{x}_{2}}^{3}\).
B├Āi 3. Theo c├Īc chuy├¬n gia vß╗ü sß╗®c khß╗Åe, nhiß╗ćt ─æß╗Ö m├┤i trŲ░ß╗Øng l├Į tŲ░ß╗¤ng nhß║źt vß╗øi cŲĪ thß╗ā cß╗¦a con ngŲ░ß╗Øi l├Ā tß╗½ 250C ─æß║┐n 280C. V├Āo buß╗Ģi s├Īng s├Īng bß║Īn Bß║Żo dß╗▒ ─æß╗ŗnh c├╣ng vß╗øi nh├│m bß║Īn ─æi d├Ż ngoß║Īi, bß║Īn sß╗Ł dß╗źng nhiß╗ćt kß║┐ ─æß╗ā ─æo nhiß╗ćt ─æß╗Ö m├┤i trŲ░ß╗Øng ng├Āy h├┤m ─æ├│ nhŲ░ sau. Vß║Ły nhiß╗ćt ─æß╗Ö n├Āy c├│ th├Łch hß╗Żp cho Bß║Żo v├Ā nh├│m bß║Īn kh├┤ng? Biß║┐t \({{T}^{0}}C=\left( {{T}^{0}}F-32 \right):1,8\]
B├Āi 4. Mß╗Öt xe tß║Żi ─æ├┤ng lß║Īnh chß╗¤ h├Āng c├│ th├╣ng xe dß║Īng h├¼nh hß╗Öp chß╗» nhß║Łt vß╗øi k├Łch thŲ░ß╗øc nhŲ░ h├¼nh b├¬n. Bß║Īn h├Ży t├Łnh gi├║p thß╗ā t├Łch cß╗¦a th├╣ng xe v├Ā diß╗ćn t├Łch phß║¦n Inox ─æ├│ng th├╣ng xe (t├Łnh lu├┤n s├Ān).
.png)
.png)
B├Āi 5. Hai c├┤ng ty Viß╗ģn th├┤ng cung cß║źp dß╗ŗch vß╗ź Internet nhŲ░ sau:
- C├┤ng ty Viß╗ģn Th├┤ng A cung cß║źp dß╗ŗch vß╗ź Internet vß╗øi mß╗®c ph├Ł ban ─æß║¦u l├Ā 480000 (Bß╗æn tr─ām t├Īm mŲ░ŲĪi ngh├¼n) ─æß╗ōng v├Ā ph├Ł hß║▒ng th├Īng l├Ā 50000 (N─ām mŲ░ŲĪi ngh├¼n) ─æß╗ōng.
- C├┤ng ty Viß╗ģn Th├┤ng B cung cß║źp dß╗ŗch vß╗ź Internet kh├┤ng t├Łnh ph├Ł ban ─æß║¦u nhŲ░ng ph├Ł hß║▒ng th├Īng l├Ā 90000 (Ch├Łn mŲ░ŲĪi ngh├¼n) ─æß╗ōng.
a) Viß║┐t 2 h├Ām sß╗æ biß╗āu thß╗ŗ mß╗®c ph├Ł khi sß╗Ł dß╗źng Internet cß╗¦a hai c├┤ng ty tr├¬n.
b) Theo bß║Īn sß╗Ł dß╗źng Internet thß╗Øi gian bao l├óu th├¼ n├¬n chß╗Źn dß╗ŗch vß╗ź b├¬n c├┤ng ty Viß╗ģn th├┤ng A c├│ lß╗Żi hŲĪn?
B├Āi 6. Ch├║ Hß║Żi l├Ā mß╗Öt kß╗╣ sŲ░ ─æiß╗ćn mß╗øi ra trŲ░ß╗Øng, xem th├┤ng tin tuyß╗ān dß╗źng cß╗¦a hai c├┤ng ty A v├Ā c├┤ng ty B. Sau khi xem th├┤ng tin tuyß╗ān dß╗źng th├¼ ch├║ Hß║Żi ─æ├Īp ß╗®ng ─æß║¦y ─æß╗¦ c├Īc y├¬u cß║¦u cß╗¦a hai c├┤ng ty, chŲ░ŲĪng tr├¼nh an sinh x├Ż hß╗Öi cß╗¦a hai c├┤ng ty c┼®ng nhŲ░ nhau, tuy nhi├¬n bß║Żn k├Į hß╗Żp ─æß╗ōng tuyß╗ān dß╗źng 1 n─ām (Sau mß╗Öt n─ām phß║Żi k├Į lß║Īi hß╗Żp ─æß╗ōng mß╗øi) th├¼ hai c├┤ng ty c├│ phŲ░ŲĪng ├Īn trß║Ż lŲ░ŲĪng kh├Īc nhau nhŲ░ sau:
- C├┤ng ty A: LŲ░ŲĪng 8 triß╗ću ─æß╗ōng mß╗Śi th├Īng v├Ā cuß╗æi mß╗Śi qu├Į ─æŲ░ß╗Żc thŲ░ß╗¤ng 27% tß╗Ģng sß╗æ tiß╗ün ─æŲ░ß╗Żc l├Żnh trong qu├Į.
- C├┤ng ty B: LŲ░ŲĪng 28,5 triß╗ću ─æß╗ōng cho qu├Į ─æß║¦u ti├¬n v├Ā mß╗Śi qu├Į sau mß╗®c lŲ░ŲĪng sß║Į t─āng th├¬m 1,2 triß╗ću ─æß╗ōng.
Em g├│p ├Į cho ch├║ Hß║Żi chß╗Źn c├┤ng ty n├Āo ─æß╗ā c├│ lß╗Żi hŲĪn ?
B├Āi 7. N─ām hß╗Źc 2018 - 2019, TrŲ░ß╗Øng Trung hß╗Źc cŲĪ sß╗¤ Th├Ānh ─É├┤ c├│ ba lß╗øp 9 gß╗ōm 9A; 9B; 9C trong ─æ├│ sß╗æ hß╗Źc sinh c├Īc lß╗øp 9A; 9B; 9C tß╗ē lß╗ć vß╗øi 3; 4; 5. Tß╗Ģng kß║┐t cuß╗æi n─ām hß╗Źc: lß╗øp 9A c├│ 50% hß╗Źc sinh ─æß║Īt danh hiß╗ću hß╗Źc sinh giß╗Åi, lß╗øp 9B c├│ 40% hß╗Źc sinh ─æß║Īt danh hiß╗ću hß╗Źc sinh giß╗Åi, c├▓n lß╗øp 9C c├│ 30% hß╗Źc sinh ─æß║Īt danh hiß╗ću hß╗Źc sinh giß╗Åi cho n├¬n tß╗Ģng sß╗æ hß╗Źc sinh ─æß║Īt danh hiß╗ću hß╗Źc sinh giß╗Åi to├Ān khß╗æi 9 l├Ā 46 em. T├Łnh sß╗æ hß╗Źc sinh cß╗¦a lß╗øp 9A; 9B; 9C cß╗¦a TrŲ░ß╗Øng Trung hß╗Źc cŲĪ sß╗¤ Th├Ānh ─É├┤ n─ām hß╗Źc 2018 - 2019.
B├Āi 8. Cho ─æŲ░ß╗Øng tr├▓n t├óm O, b├Īn k├Łnh R; ─æŲ░ß╗Øng k├Łnh AB v├Ā ─æiß╗ām M bß║źt kß╗│ thuß╗Öc (O). Tiß║┐p tuyß║┐n tß║Īi M cß╗¦a (O) cß║»t tiß║┐p tuyß║┐n tß║Īi A, B cß╗¦a (O) lß║¦n lŲ░ß╗Żt tß║Īi C v├Ā D.
a) Chß╗®ng minh: CD=AC+BD v├Ā \(\Delta \ COD\) l├Ā tam gi├Īc vu├┤ng.
b) Gß╗Źi E l├Ā giao ─æiß╗ām cß╗¦a OC vß╗øi AM v├Ā F l├Ā giao ─æiß╗ām cß╗¦a OD vß╗øi BM. Chß╗®ng minh: tß╗® gi├Īc CEFD l├Ā tß╗® gi├Īc nß╗Öi tiß║┐p.
c) Cho \(AC=\frac{R\sqrt{3}}{3}\). Gß╗Źi I l├Ā giao ─æiß╗ām cß╗¦a AD vß╗øi BC, MI cß║»t OC tß║Īi K. T├Łnh sß╗æ ─æo cß╗¦a g├│c \(\widehat{KAM}\).
---(─Éß╗ā xem tiß║┐p nß╗Öi dung cß╗¦a ─æß╗ü thi sß╗æ 4 c├Īc em vui l├▓ng xem tß║Īi online hoß║Ęc ─æ─āng nhß║Łp v├Āo Hß╗īC247 ─æß╗ā tß║Żi vß╗ü m├Īy)---
─Éß╗Ć Sß╗É 5
─Éß╗Ć THI THß╗¼ V├ĆO Lß╗ÜP 10 M├öN TO├üN TRŲ»ß╗£NG THCS T├ö HO├ĆNG- ─Éß╗Ć 05
B├Āi 1:
Cho h├Ām sß╗æ (P): y= -1/2x2 v├Ā (D): y = x ŌĆō 4
a) Vß║Į (P) v├Ā (D) tr├¬n c├╣ng hß╗ć trß╗źc tß╗Źa ─æß╗Ö.
b) T├¼m tß╗Źa ─æß╗Ö giao ─æiß╗ām cß╗¦a (P) v├Ā (D) bß║▒ng ph├®p t├Łnh.
B├Āi 2:
Cho phŲ░ŲĪng tr├¼nh : 3x2 + 5x ŌĆō 6 = 0 c├│ 2 nghiß╗ćm l├Ā x1, x2.
Kh├┤ng giß║Żi phŲ░ŲĪng tr├¼nh, h├Ży t├Łnh gi├Ī trß╗ŗ biß╗āu thß╗®c A =(x1 - 2x2)( 2x1 - x2)
B├Āi 3: B├Īc An cß║¦n l├Īt gß║Īch mß╗Öt nß╗ün nh├Ā h├¼nh chß╗» nhß║Łt c├│ chu vi l├Ā 48m v├Ā chiß╗üu d├Āi hß╗Żn chiß╗üu rß╗Öng l├Ā 12m. B├Īc An chß╗Źn gß║Īch h├¼nh vu├┤ng c├│ cß║Īnh l├Ā 60cm ─æß╗ā l├Īt gß║Īch nß╗ün nh├Ā, gi├Ī mß╗Śi vi├¬n gß║Īch l├Ā 120 000 ─æß╗ōng. Hß╗Åi b├Īc An cß║¦n bao nhi├¬u tiß╗ün ─æß╗ā l├Īt gß║Īch nß╗ün nh├Ā?
B├Āi 4: Mß╗Öt ph├▓ng hß╗Źp c├│ 80 ghß║┐ ngß╗ōi, ─æŲ░ß╗Żc xß║┐p th├Ānh tß╗½ng h├Āng, mß╗Śi h├Āng c├│ sß╗æ lŲ░ß╗Żng ghß║┐ bß║▒ng nhau. Nß║┐u bß╗øt di 2 h├Āng m├Ā kh├┤ng l├Ām thay ─æß╗Ģi sß╗æ lŲ░ß╗Żng ghß║┐ trong ph├▓ng th├¼ mß╗Śi h├Āng c├▓n lß║Īi phß║Żi xß║┐p th├¬m 2 ghß║┐. Hß╗Åi l├║c ─æß║¦u trong ph├▓ng c├│ bao nhi├¬u h├Āng ghß║┐ ?
B├Āi 5: Bß║Īn An ─æi xe bu├Įt ─æß║┐n cß╗Ła h├Āng ─æß╗ā mua x quyß╗ān tß║Łp, gi├Ī mß╗Śi quyß╗ān tß║Łp l├Ā a (─æß╗ōng), gß╗Źi b (─æß╗ōng) l├Ā chi ph├Ł xe bu├Įt cß║Ż ─æi lß║½n vß╗ü. H├Ām sß╗æ bß║Łc nhß║źt y biß╗āu diß╗ģn tß╗Ģng sß╗æ tiß╗ün bß║Īn An phß║Żi tß╗æn khi ─æi mua tß║Łp cß╗¦a cß╗Ła h├Āng c├│ ─æß╗ō thß╗ŗ nhŲ░ sau:
.png)
a) H├Ży viß║┐t h├Ām sß╗æ y biß╗āu diß╗ģn tß╗Ģng sß╗æ tiß╗ün bß║Īn An phß║Żi tß╗æn khi ─æi mua tß║Łp cß╗¦a cß╗Ła h├Āng v├Ā dß╗▒a v├Āo ─æß╗ō thß╗ŗ x├Īc ─æß╗ŗnh c├Īc hß╗ć sß╗æ b v├Ā a.
b) Nß║┐u tß╗Ģng sß╗æ tiß╗ün y (─æß╗ōng) bß║Īn An phß║Żi tß╗æn l├Ā 84 ng├Ān (─æß╗ōng) th├¼ bß║Īn An mua ─æŲ░ß╗Żc bao nhi├¬u cuß╗æn tß║Łp ?
B├Āi 6: Mß╗Öt hß╗ō bŲĪi c├│ dß║Īng l├Ā mß╗Öt l─āng trß╗ź ─æß╗®ng tß╗® gi├Īc vß╗øi ─æ├Īy l├Ā h├¼nh thang vu├┤ng (mß║Ęt b├¬n (1) cß╗¦a hß╗ō bŲĪi l├Ā 1 ─æ├Īy cß╗¦a l─āng trß╗ź) v├Ā c├Īc k├Łch thŲ░ß╗øc nhŲ░ ─æ├Ż cho (xem h├¼nh vß║Į). Biß║┐t rß║▒ng ngŲ░ß╗Øi ta d├╣ng mß╗Öt m├Īy bŲĪm vß╗øi lŲ░u lŲ░ß╗Żng l├Ā 42 m3/ph├║t v├Ā sß║Į bŲĪm ─æß║¦y hß╗ō mß║źt 25 ph├║t. T├Łnh chiß╗üu d├Āi cß╗¦a hß╗ō.
B├Āi 7: Bß║Īn An trung b├¼nh ti├¬u thß╗ź 18 calo cho mß╗Śi ph├║t bŲĪi v├Ā 12 calo cho mß╗Śi ph├║t chß║Īy bß╗Ö. H├┤m nay , An mß║źt 2,75 giß╗Ø cho cß║Ż hai hoß║Īt ─æß╗Öng tr├¬n v├Ā ti├¬u thß╗ź hß║┐t 2520 calo. Hß╗Åi h├┤m nay, bß║Īn An mß║źt bao nhi├¬u thß╗Øi gian cho mß╗Śi hoß║Īt ─æß╗Öng.
C├óu 8. Cho ─æŲ░ß╗Øng tr├▓n (O ; R) v├Ā ─æiß╗ām S nß║▒m ngo├Āi ─æŲ░ß╗Øng tr├▓n (O) (SO < 2R). Tß╗½ S vß║Į hai tiß║┐p tuyß║┐n SA , SB (A, B l├Ā tiß║┐p ─æiß╗ām) v├Ā c├Īt tuyß║┐n SMN kh├┤ng qua t├óm (M nß║▒m giß╗»a S v├Ā N) tß╗øi ─æŲ░ß╗Øng tr├▓n (O).
a) Chß╗®ng minh: SA2 = SM.SN.
b) Gß╗Źi I l├Ā trung ─æiß╗ām cß╗¦a MN. Chß╗®ng minh: IS l├Ā ph├ón gi├Īc cß╗¦a g├│c AIB.
c) Gß╗Źi H l├Ā giao ─æiß╗ām cß╗¦a AB v├Ā SO. Hai ─æŲ░ß╗Øng thß║│ng OI v├Ā BA cß║»t nhau tß║Īi E.
Chß╗®ng minh: OI.OE = R2.
---(─Éß╗ā xem tiß║┐p nß╗Öi dung cß╗¦a ─æß╗ü thi sß╗æ 5 c├Īc em vui l├▓ng xem tß║Īi online hoß║Ęc ─æ─āng nhß║Łp v├Āo Hß╗īC247 ─æß╗ā tß║Żi vß╗ü m├Īy)---
Tr├¬n ─æ├óy l├Ā mß╗Öt phß║¦n tr├Łch ─æoß║Īn nß╗Öi dung Bß╗Ö 5 ─æß╗ü thi thß╗Ł v├Āo lß╗øp 10 m├┤n To├Īn n─ām 2022-2023 c├│ ─æ├Īp ├Īn TrŲ░ß╗Øng THCS T├┤ Ho├Āng. ─Éß╗ā xem to├Ān bß╗Ö nß╗Öi dung c├Īc em chß╗Źn chß╗®c n─āng xem online hoß║Ęc ─æ─āng nhß║Łp v├Āo trang hoc247.net ─æß╗ā tß║Żi t├Āi liß╗ću vß╗ü m├Īy t├Łnh.
Mß╗Øi c├Īc em tham khß║Żo t├Āi liß╗ću c├│ li├¬n quan:
- Bß╗Ö 5 ─æß╗ü thi thß╗Ł v├Āo lß╗øp 10 m├┤n To├Īn n─ām 2022-2023 c├│ ─æ├Īp ├Īn TrŲ░ß╗Øng THCS Hß╗ō Thß╗ŗ HŲ░ŲĪng
- Bß╗Ö 5 ─æß╗ü thi thß╗Ł v├Āo lß╗øp 10 m├┤n To├Īn n─ām 2022-2023 c├│ ─æ├Īp ├Īn TrŲ░ß╗Øng THCS Phß║Īm Ngß╗Źc Thß║Īch
Hy vß╗Źng bß╗Ö ─æß╗ü thi n├Āy sß║Į gi├║p c├Īc em hß╗Źc sinh ├┤n tß║Łp tß╗æt v├Ā ─æß║Īt th├Ānh t├Łch cao trong k├¼ thi sß║»p tß╗øi.
T├Āi liß╗ću li├¬n quan
TŲ░ liß╗ću nß╗Ģi bß║Łt tuß║¦n
- Xem thêm





.JPG?enablejsapi=1)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)