DŲ░ß╗øi ─æ├óy l├Ā nß╗Öi dung Bß╗Ö 4 ─æß╗ü thi thß╗Ł THPT QG n─ām 2021 m├┤n To├Īn - TrŲ░ß╗Øng THPT Triß╗ću SŲĪn ─æŲ░ß╗Żc hoc247 bi├¬n soß║Īn v├Ā tß╗Ģng hß╗Żp, vß╗øi nß╗Öi dung ─æß║¦y ─æß╗¦, chi tiß║┐t c├│ ─æ├Īp ├Īn ─æi k├©m sß║Į gi├║p c├Īc em hß╗Źc sinh ├┤n tß║Łp cß╗¦ng cß╗æ kiß║┐n thß╗®c, n├óng cao kß╗╣ n─āng l├Ām b├Āi. Mß╗Øi c├Īc em c├╣ng tham khß║Żo!
|
TRŲ»ß╗£NG THPT TRIß╗åU SŲĀN |
─Éß╗Ć THI THPT QG N─éM Hß╗īC 2021 M├öN: TO├üN Thß╗Øi gian: 90 ph├║t |
1. ─Éß╗Ć Sß╗É 1
C├óu 1: Cho h├¼nh ch├│p \(S.ABCD\) c├│ ─æ├Īy \(ABCD\) l├Ā h├¼nh vu├┤ng cß║Īnh \(a,\) cß║Īnh b├¬n \(SA\) vu├┤ng g├│c vß╗øi ─æ├Īy v├Ā \(SA = 2a.\) Gß╗Źi \(B',\,\,D'\) lß║¦n lŲ░ß╗Żt l├Ā h├¼nh chiß║┐u vu├┤ng g├│c cß╗¦a \(A\) tr├¬n c├Īc cß║Īnh \(SB,\,\,SD.\) Mß║Ęt phß║│ng \(\left( {AB'D'} \right)\) cß║»t cß║Īnh \(SC\) tß║Īi \(C'.\) T├Łnh thß╗ā t├Łch khß╗æi ch├│p \(S.AB'C'D'.\)
A. \(\dfrac{{{a^3}}}{3}.\)
B. \(\dfrac{{16{a^3}}}{{45}}.\)
C. \(\dfrac{{{a^3}}}{2}.\)
D. \(\dfrac{{{a^3}\sqrt 2 }}{4}.\)
C├óu 2: H├¼nh ─æa diß╗ćn n├Āo dŲ░ß╗øi ─æ├óy kh├┤ng c├│ t├óm ─æß╗æi xß╗®ng ?
A. H├¼nh l─āng trß╗ź tß╗® gi├Īc ─æß╗üu.
B. H├¼nh b├Īt diß╗ćn ─æß╗üu.
C. H├¼nh tß╗® diß╗ćn ─æß╗üu.
D. H├¼nh lß║Łp phŲ░ŲĪng.
C├óu 3: C├│ tß║źt cß║Ż bao nhi├¬u cß║Ęp sß╗æ nguy├¬n chß║Ąn \(\left( {x;y} \right)\) thß╗Åa m├Żn \({2^x} - {3^y} = 55\,\,?\)
A. 8.
B. 2.
C. 16.
D. 1.
C├óu 4: Gß╗Źi \(S\) l├Ā tß║Łp hß╗Żp c├Īc sß╗æ thß╗▒c \(\left( {x;y} \right)\) sao cho \(x \in \left[ { - \,1;1} \right]\) v├Ā thß╗Åa m├Żn ─æiß╗üu kiß╗ćn \(\ln {\left( {x - y} \right)^x} - 2017x = \ln {\left( {x - y} \right)^y} - 2017y + {e^{2018}}.\) Biß║┐t gi├Ī trß╗ŗ lß╗øn nhß║źt cß╗¦a biß╗āu thß╗®c \(P = {e^{2018x}}\left( {y + 1} \right) - 2018{x^2}\) vß╗øi \(\left( {x;y} \right) \in S\) ─æß║Īt ─æŲ░ß╗Żc tß║Īi \(\left( {{x_0};{y_0}} \right).\) Mß╗ćnh ─æß╗ü n├Āo sau ─æ├óy ─æ├║ng ?
A. \({x_0} \in \left( { - \,1;0} \right).\)
B. \({x_0} = - \,1.\)
C. \({x_0} = 1.\)
D. \({x_0} \in \left[ {0;1} \right).\)
C├óu 5: Trong mß║Ęt phß║│ng cho g├│c \(xOy.\) Mß╗Öt mß║Ęt phß║│ng \(\left( P \right)\) thay ─æß╗Ģi v├Ā vu├┤ng g├│c vß╗øi ─æŲ░ß╗Øng ph├ón gi├Īc trong cß╗¦a g├│c \(xOy\) cß║»t \(Ox,\,\,Oy\) lß║¦n lŲ░ß╗Żt tß║Īi \(A,\,\,B.\) Trong \(\left( P \right)\) lß║źy ─æiß╗ām \(M\) sao cho \(\widehat {AMB} = {90^0}.\) Mß╗ćnh ─æß╗ü n├Āo sau ─æ├óy l├Ā ─æ├║ng ?
A. ─Éiß╗ām \(M\) chß║Īy tr├¬n mß╗Öt mß║Ęt cß║¦u.
B. ─Éiß╗ām \(M\) chß║Īy tr├¬n mß╗Öt mß║Ęt n├│n.
C. ─Éiß╗ām \(M\) chß║Īy tr├¬n mß╗Öt mß║Ęt trß╗ź.
D. ─Éiß╗ām \(M\) chß║Īy tr├¬n mß╗Öt ─æŲ░ß╗Øng tr├▓n.
C├óu 6: N─ām 1992, ngŲ░ß╗Øi ta ─æ├Ż biß║┐t sß╗æ \(p = {2^{756839}} - 1\) l├Ā mß╗Öt sß╗æ nguy├¬n tß╗æ (sß╗æ nguy├¬n tß╗æ lß╗øn nhß║źt ─æŲ░ß╗Żc biß║┐t cho ─æß║┐n l├║c ─æ├│). H├Ży t├¼m sß╗æ c├Īc chß╗» sß╗æ cß╗¦a \(p\) khi viß║┐t trong hß╗ć thß║Łp ph├ón.
A. 227830 chữ số.
B. 227834 chữ số.
C. 227832 chữ số.
D. 227831 chữ số.
C├óu 7: C├│ tß║źt cß║Ż bao nhi├¬u gi├Ī trß╗ŗ nguy├¬n cß╗¦a tham sß╗æ \(m\) ─æß╗ā h├Ām sß╗æ \(y = \ln \left( {{x^2} - 2mx + 4} \right)\) c├│ tß║Łp x├Īc ─æß╗ŗnh l├Ā \(\mathbb{R}\,?\)
A. 1.
B. 0.
C. 5.
D. 3.
C├óu 8: C├│ mŲ░ß╗Øi c├Īi ghß║┐ (mß╗Śi ghß║┐ chß╗ē ngß╗ōi ─æŲ░ß╗Żc mß╗Öt ngŲ░ß╗Øi) ─æŲ░ß╗Żc sß║»p tr├¬n mß╗Öt h├Āng ngang. Xß║┐p ngß║½u nhi├¬n 7 hß╗Źc sinh ngß╗ōi v├Āo, mß╗Śi hß╗Źc sinh ngß╗ōi ─æ├║ng mß╗Öt ghß║┐. T├Łnh x├Īc suß║źt sao cho kh├┤ng c├│ hai ghß║┐ trß╗æng n├Āo kß╗ü nhau.
A. 0,25.
B. 0,46.
C. 0,6(4).
D. 0,4(6).
C├óu 9: ─ÉŲ░ß╗Øng thß║│ng \(AM\) tß║Īo vß╗øi mß║Ęt phß║│ng chß╗®a tam gi├Īc ─æß╗üu \(ABC\) mß╗Öt g├│c \({60^0}.\) Biß║┐t rß║▒ng cß║Īnh cß╗¦a tam gi├Īc ─æß╗üu bß║▒ng \(a\) v├Ā \(\widehat {MAB} = \widehat {MAC}.\) T├Łnh khoß║Żng c├Īch giß╗»a hai ─æŲ░ß╗Øng thß║│ng \(AM\) v├Ā \(BC.\)
A. \(\dfrac{{3a}}{4}.\)
B. \(\dfrac{{a\sqrt 2 }}{2}.\)
C. \(a.\)
D. \(\dfrac{{a\sqrt 3 }}{2}.\)
C├óu 10: T├Łnh tß╗Ģng tß║źt cß║Ż c├Īc nghiß╗ćm thuß╗Öc khoß║Żng \(\left( {0;2\pi } \right)\) cß╗¦a phŲ░ŲĪng tr├¼nh \({\sin ^4}\dfrac{x}{2} + {\cos ^4}\dfrac{x}{2} = \dfrac{5}{8}.\)
A. \(\dfrac{{9\pi }}{8}.\)
B. \(\dfrac{{12\pi }}{3}.\)
C. \(\dfrac{{9\pi }}{4}.\)
D. \(2\pi .\)
ĐÁP ÁN
|
1. B |
2. C |
3. D |
4. A |
5. B |
|
6. C |
7. D |
8. D |
9. A |
10. B |
{-- Nß╗Öi dung ─æß╗ü, ─æ├Īp ├Īn tß╗½ c├óu 11-50 c├Īc em vui l├▓ng xem ß╗¤ phß║¦n xem online hoß║Ęc tß║Żi vß╗ü --}
2. ─Éß╗Ć Sß╗É 2
C├óu 1: Cho h├Ām sß╗æ \(f\left( x \right) = {\left( {\dfrac{1}{2}} \right)^x}{.5^{{x^2}}}.\) Khß║│ng ─æß╗ŗnh n├Āo sau ─æ├óy l├Ā sai?
A. \(f\left( x \right) > 1 \Leftrightarrow {x^2} + x{\log _2}5 > 0.\)
B. \(f\left( x \right) > 1 \Leftrightarrow x - {x^2}{\log _2}5 < 0.\)
C. \(f\left( x \right) > 1 \Leftrightarrow {x^2} - x{\log _5}2 > 0.\)
D. \(f\left( x \right) > 1 \Leftrightarrow - \,x\ln 2 + {x^2}\ln 5 > 0.\)
C├óu 2: Cho mß╗Öt tam gi├Īc, tr├¬n ba cß║Īnh cß╗¦a n├│ lß║źy 9 ─æiß╗ām nhŲ░ h├¼nh vß║Į. C├│ tß║źt cß║Ż bao nhi├¬u tam gi├Īc c├│ ba ─æß╗ēnh thuß╗Öc 9 ─æiß╗ām ─æ├Ż cho?
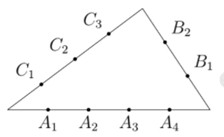
A. 79.
B. 48.
C. 55.
D. 24.
C├óu 3: T├¼m tß║Łp x├Īc ─æß╗ŗnh \(D\) cß╗¦a h├Ām sß╗æ \(y = \tan \left( {2x - \dfrac{\pi }{4}} \right).\)
A. \(D = \mathbb{R}\backslash \left\{ {\dfrac{{3\pi }}{8} + \dfrac{{k\pi }}{2},\,\,k \in \mathbb{Z}} \right\}.\)
B. \(D = \mathbb{R}\backslash \left\{ {\dfrac{{3\pi }}{4} + k\pi ,\,\,k \in \mathbb{Z}} \right\}.\)
C. \(D = \mathbb{R}\backslash \left\{ {\dfrac{{3\pi }}{4} + \dfrac{{k\pi }}{2},\,\,k \in \mathbb{Z}} \right\}.\)
D. \(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k\pi ,\,\,k \in \mathbb{Z}} \right\}.\)
C├óu 4: Trong c├Īc mß╗ćnh ─æß╗ü sau, mß╗ćnh ─æß╗ü n├Āo sau ─æ├óy l├Ā sai ?
A. Khoß║Żng c├Īch giß╗»a hai ─æŲ░ß╗Øng thß║│ng ch├®o nhau bß║▒ng khoß║Żng c├Īch giß╗»a ─æŲ░ß╗Øng thß║│ng n├Āy v├Ā mß║Ęt phß║│ng song song vß╗øi n├│ ─æß╗ōng thß╗Øi chß╗®a ─æŲ░ß╗Øng thß║│ng kia.
B. Khoß║Żng c├Īch giß╗»a hai ─æŲ░ß╗Øng thß║│ng ch├®o nhau bß║▒ng khoß║Żng c├Īch giß╗»a hai mß║Ęt phß║│ng song song lß║¦n lŲ░ß╗Żt chß╗®a hai ─æŲ░ß╗Øng thß║│ng ─æ├│.
C. Khoß║Żng c├Īch giß╗»a hai ─æŲ░ß╗Øng thß║│ng ch├®o nhau bß║▒ng khoß║Żng c├Īch tß╗½ mß╗Öt ─æiß╗ām bß║źt k├¼ thuß╗Öc ─æŲ░ß╗Øng thß║│ng n├Āy ─æß║┐n ─æŲ░ß╗Øng thß║│ng kia.
D. Khoß║Żng c├Īch giß╗»a hai ─æŲ░ß╗Øng thß║│ng ch├®o nhau l├Ā ─æß╗Ö d├Āi ─æoß║Īn vu├┤ng g├│c chung cß╗¦a hai ─æŲ░ß╗Øng thß║│ng ─æ├│.
C├óu 5: C├│ tß║źt cß║Ż nao nhi├¬u gi├Ī trß╗ŗ nguy├¬n cß╗¦a tham sß╗æ \(m\) ─æß╗ā h├Ām sß╗æ \(f\left( x \right) = \dfrac{m}{3}{x^3} - 2m{x^2} + \left( {3m + 5} \right)x\) ─æß╗ōng biß║┐n tr├¬n \(\mathbb{R}?\)
A. \(6.\)
B. \(2.\)
C. \(5.\)
D. \(4.\)
C├óu 6: Trong c├Īc mß╗ćnh ─æß╗ü sau, mß╗ćnh ─æß╗ü n├Āo ─æ├║ng ?
A. Tß╗ōn tß║Īi mß╗Öt h├¼nh ─æa diß╗ćn c├│ sß╗æ cß║Īnh bß║▒ng sß╗æ ─æß╗ēnh.
B. Tß╗ōn tß║Īi mß╗Öt h├¼nh ─æa diß╗ćn c├│ sß╗æ cß║Īnh v├Ā sß╗æ mß║Ęt bß║▒ng nhau.
C. Sß╗æ ─æß╗ēnh v├Ā sß╗æ mß║Ęt cß╗¦ h├¼nh ─æa diß╗ćn lu├┤n bß║▒ng nhau.
D. Tß╗ōn tß║Īi mß╗Öt h├¼nh ─æa diß╗ćn c├│ sß╗æ ─æß╗ēnh v├Ā sß╗æ mß║Ęt bß║▒ng nhau.
C├óu 7: Cho h├Ām sß╗æ \(y = f\left( x \right)\) c├│ ─æß╗ō thß╗ŗ tr├¬n ─æoß║Īn \(\left[ { - \,2;4} \right]\) nhŲ░ h├¼nh vß║Į b├¬n. T├¼m \(\mathop {\max }\limits_{\left[ { - \,2;4} \right]} \left| {f\left( x \right)} \right|.\)
A. \(\left| {f\left( 0 \right)} \right|.\)
B. 2.
C. 3.
D. 1.
C├óu 8: ─Éß╗ō thß╗ŗ h├Ām sß╗æ \(y = \dfrac{{\sqrt {{x^2} - 4} }}{{{x^2} - 5x + 6}}\) c├│ tß║źt cß║Ż bao nhi├¬u ─æŲ░ß╗Øng tiß╗ćm cß║Łn ?
A. 1.
B. 3.
C. 4.
D. 2.
C├óu 9: Biß║┐t tß║Łp nghiß╗ćm \(S\) cß╗¦a bß║źt phŲ░ŲĪng tr├¼nh \({\log _{\dfrac{\pi }{6}}}\left[ {{{\log }_3}\left( {x - 2} \right)} \right] > 0\) l├Ā khoß║Żng \(\left( {a;b} \right).\) T├Łnh \(b - a.\)
A. 2.
B. 4.
C. 3.
D. 5.
C├óu 10: Cho h├Ām sß╗æ \(y = {x^4} - 2{x^2} + 3x + 1\) c├│ ─æß╗ō thß╗ŗ \(\left( C \right).\) C├│ tß║źt cß║Ż bao nhi├¬u tiß║┐p tuyß║┐n cß╗¦a ─æß╗ō thß╗ŗ \(\left( C \right)\) song song vß╗øi ─æŲ░ß╗Øng thß║│ng \(y = 3x + 2018\) ?
A. 2.
B. 3.
C. 1.
D. 4.
ĐÁP ÁN
|
1. A |
2. A |
3. D |
4. C |
5. A |
|
6. D |
7. C |
8. B |
9. A |
10. B |
{-- Nß╗Öi dung ─æß╗ü, ─æ├Īp ├Īn tß╗½ c├óu 11-50 c├Īc em vui l├▓ng xem ß╗¤ phß║¦n xem online hoß║Ęc tß║Żi vß╗ü --}
3. ─Éß╗Ć Sß╗É 3
C├óu 1: Trong c├Īc mß╗ćnh ─æß╗ü sau, mß╗ćnh ─æß╗ü n├Āo sau ─æ├óy sai ?
A. Hai khß╗æi lß║Łp phŲ░ŲĪng c├│ diß╗ćn t├Łch to├Ān phß║¦n bß║▒ng nhau th├¼ c├│ thß╗ā t├Łch bß║▒ng nhau.
B. Hai khß╗æi hß╗Öp chß╗» nhß║Łt c├│ diß╗ćn t├Łch to├Ān phß║¦n bß║▒ng nhau th├¼ c├│ thß╗ā bß║▒ng nhau.
C. Thß╗ā t├Łch cß╗¦a hai khß╗æi ch├│p c├│ diß╗ćn t├Łch ─æ├Īy v├Ā chiß╗üu cao tŲ░ŲĪng ß╗®ng bß║▒ng nhau l├Ā bß║▒ng nhau.
D. Thß╗ā t├Łch cß╗¦a khß╗æi l─āng trß╗ź bß║▒ng diß╗ćn t├Łch ─æ├Īy nh├ón vß╗øi chiß╗üu cao.
C├óu 2: Cho h├¼nh ch├│p tß╗® gi├Īc ─æß╗üu c├│ cß║Īnh ─æ├Īy bß║▒ng 1 v├Ā chiß╗üu cao bß║▒ng 2. X├®t h├¼nh ─æa diß╗ćn lß╗ōi H c├│ c├Īc ─æß╗ēnh l├Ā trung ─æiß╗ām cß╗¦a tß║źt cß║Ż c├Īc cß║Īnh cß╗¦a h├¼nh ch├│p ─æ├│. T├Łnh thß╗ā t├Łch cß╗¦a H.
A. \(\dfrac{9}{2}.\)
B. \(4.\)
C. \(2\sqrt 3 .\)
D. \(\dfrac{5}{{12}}.\)
C├óu 3: Cho \(a\) l├Ā sß╗æ thß╗▒c dŲ░ŲĪng. Biß║┐t \(F\left( x \right)\) l├Ā mß╗Öt nguy├¬n h├Ām cß╗¦a h├Ām sß╗æ \(f\left( x \right) = {e^x}\left[ {\ln \left( {ax} \right) + \dfrac{1}{x}} \right]\) thß╗Åa m├Żn \(F\left( {\dfrac{1}{a}} \right) = 0\) v├Ā \(F\left( {2018} \right) = {e^{2018}}.\) Mß╗ćnh ─æß╗ü n├Āo sau ─æ├óy ─æ├║ng ?
A. \(a \in \left( {\dfrac{1}{{2018}};1} \right).\)
B. \(a \in \left( {0;\dfrac{1}{{2018}}} \right].\)
C. \(a \in \left[ {1;2018} \right).\)
D. \(a \in \left[ {2018; + \,\infty } \right).\)
C├óu 4: Khß╗æi l─āng trß╗ź ng┼® gi├Īc c├│ tß║źt cß║Ż bao nhi├¬u cß║Īnh ?
A. 20.
B. 25.
C. 10.
D. 15.
C├óu 5: C├│ tß║źt cß║Ż bao nhi├¬u c├Īch chia 10 ngŲ░ß╗Øi th├Ānh hai nh├│m, mß╗Öt nh├│m c├│ 6 ngŲ░ß╗Øi v├Ā mß╗Öt nh├│m c├│ 4 ngŲ░ß╗Øi ?
A. 210.
B. 120.
C. 100.
D. 140.
C├óu 6: T├¼m hß╗Ź nguy├¬n h├Ām cß╗¦a h├Ām sß╗æ \(f\left( x \right) = \tan 2x.\)
A. \(\int {\tan 2x\,{\rm{d}}x} = 2\left( {1 + {{\tan }^2}2x} \right) + C.\)
B. \(\int {\tan 2x\,{\rm{d}}x} = - \,\ln \left| {\cos 2x} \right| + C.\)
C. \(\int {\tan 2x\,{\rm{d}}x} = \dfrac{1}{2}\left( {1 + {{\tan }^2}2x} \right) + C.\)
D. \(\int {\tan 2x\,{\rm{d}}x} = - \,\dfrac{1}{2}\ln \left| {\cos 2x} \right| + C.\)
C├óu 7: Cho h├Ām sß╗æ \(y = {x^3} - 3{x^2} + 2x.\) C├│ tß║źt cß║Ż bao nhi├¬u tiß║┐p tuyß║┐n cß╗¦a ─æß╗ō thß╗ŗ h├Ām sß╗æ ─æi qua ─æiß╗ām \(A\left( { - \,1;0} \right)\) ?
A. 1.
B. 2.
C. 3.
D. 4.
C├óu 8: H├¼nh b├Īt diß╗ćn ─æß╗üu c├│ tß║źt cß║Ż bao nhi├¬u mß║Ęt phß║│ng ─æß╗æi xß╗®ng ?
A. 5.
B. 6.
C. 9.
D. 8.
C├óu 9: R├║t gß╗Źn biß╗āu thß╗®c \(P = {x^{\dfrac{1}{3}}}.\sqrt[6]{x}\) vß╗øi \(x > 0.\)
A. \(P = \sqrt x .\)
B. \(P = {x^{\dfrac{1}{8}}}.\)
C. \(P = {x^{\dfrac{2}{9}}}.\)
D. \(P = {x^2}.\)
C├óu 10: T├¼m hß╗Ź nguy├¬n h├Ām cß╗¦a h├Ām sß╗æ \(f\left( x \right) = {5^{2x}}.\)
A. \(\int {{5^{2x}}\,{\rm{d}}x} = 2.\dfrac{{{5^{2x}}}}{{\ln 5}} + C.\)
B. \(\int {{5^{2x}}\,{\rm{d}}x} = \dfrac{{{{25}^x}}}{{2\ln 5}} + C.\)
C. \(\int {{5^{2x}}\,{\rm{d}}x} = {2.5^{2x}}\ln 5 + C.\)
D. \(\int {{5^{2x}}\,{\rm{d}}x} = \dfrac{{{{25}^{x\, + \,1}}}}{{x + 1}} + C.\)
ĐÁP ÁN
|
1. B |
2. D |
3. A |
4. D |
5. A |
|
6. D |
7. C |
8. C |
9. A |
10. B |
{-- Nß╗Öi dung ─æß╗ü, ─æ├Īp ├Īn tß╗½ c├óu 11-50 c├Īc em vui l├▓ng xem ß╗¤ phß║¦n xem online hoß║Ęc tß║Żi vß╗ü --}
4. ─Éß╗Ć Sß╗É 4
C├óu 1: Mß╗Öt h├¼nh ch├│p c├│ ─æ├Īy l├Ā tam gi├Īc ─æß╗üu cß║Īnh bß║▒ng 2 v├Ā chiß╗üu cao bß║▒ng 4. T├Łnh thß╗ā t├Łch cß╗¦a h├¼nh ch├│p ─æ├│.
A. \(4.\)
B. \(\dfrac{{4\sqrt 3 }}{3}.\)
C. \(2\sqrt 3 .\)
D. \(2.\)
C├óu 2: Trong kh├┤ng gian, cho hai ─æiß╗ām \(A,\,\,B\) cß╗æ ─æß╗ŗnh, ph├ón biß╗ćt v├Ā ─æiß╗ām \(M\) thay ─æß╗Ģi sao cho diß╗ćn t├Łch tam gi├Īc \(MAB\) kh├┤ng ─æß╗Ģi. Trong c├Īc mß╗ćnh ─æß╗ü sau, mß╗ćnh ─æß╗ü n├Āo ─æ├║ng ?
A. Tß║Łp hß╗Żp c├Īc ─æiß╗ām \(M\) l├Ā mß╗Öt mß║Ęt phß║│ng.
B. Tß║Łp hß╗Żp c├Īc ─æiß╗ām \(M\) l├Ā mß╗Öt mß║Ęt trß╗ź.
C. Tß║Łp hß╗Żp c├Īc ─æiß╗ām \(M\) l├Ā mß╗Öt mß║Ęt n├│n.
D. Tß║Łp hß╗Żp c├Īc ─æiß╗ām \(M\) l├Ā mß╗Öt mß║Ęt cß║¦u.
C├óu 3: Cho h├Ām sß╗æ \(f\left( x \right) = \sin x + \cos x\) c├│ ─æß╗ō thß╗ŗ \(\left( C \right).\) Trong c├Īc h├Ām sß╗æ sau, h├Ām sß╗æ n├Āo c├│ ─æß╗ō thß╗ŗ kh├┤ng thß╗ā thu ─æŲ░ß╗Żc bß║▒ng c├Īch tß╗ŗnh tiß║┐n ─æß╗ō thß╗ŗ \(\left( C \right)\) ?
A. \(y = \sin x - \cos x.\)
B. \(y = \left| {\sqrt 2 \sin x + \sqrt 2 } \right|.\)
C. \(y = - \,\sin x - \cos x.\)
D. \(y = \sin \left( {x + \dfrac{\pi }{4}} \right).\)
C├óu 4: C├│ tß║źt cß║Ż bao nhi├¬u bß╗Ö ba sß╗æ thß╗▒c \(\left( {x;y;z} \right)\) thß╗Åa m├Żn ─æß╗ōng thß╗Øi c├Īc ─æiß╗üu kiß╗ćn dŲ░ß╗øi ─æ├óy
\({2^{\sqrt[3]{{{x^2}}}}}{.4^{\sqrt[3]{{{y^2}}}}}{.16^{\sqrt[3]{{{z^2}}}}} = 128\) v├Ā \({\left( {x{y^2} + {z^4}} \right)^2} = 4 + {\left( {x{y^2} - {z^4}} \right)^2}\)
A. 3.
B. 4.
C. 1.
D. 2.
C├óu 5: Cho h├¼nh l─āng trß╗ź ─æß╗®ng c├│ chiß╗üu cao bß║▒ng \(h\) kh├┤ng ─æß╗Ģi, mß╗Öt ─æ├Īy l├Ā tß╗® gi├Īc \(ABCD\) vß╗øi \(A,\) \(B,\) \(C,\) \(D\) di ─æß╗Öng. Gß╗Źi \(I\) l├Ā giao ─æiß╗ām cß╗¦a hai ─æŲ░ß╗Øng ch├®o \(AC\) v├Ā \(BD.\) Cho biß║┐t \(IA.IC = IB.ID = {h^2}.\) T├Łnh gi├Ī trß╗ŗ nhß╗Å nhß║źt cß╗¦a b├Īn k├Łnh mß║Ęt cß║¦u ngoß║Īi tiß║┐p h├¼nh l─āng trß╗ź ─æ├Ż cho.
A. \(2h.\)
B. \(\dfrac{{h\sqrt 5 }}{2}.\)
C. \(h.\)
D. \(\dfrac{{h\sqrt 3 }}{2}.\)
C├óu 6: Cho h├Ām sß╗æ \(y = f\left( x \right)\) c├│ ─æß║Īo h├Ām tr├¬n khoß║Żng \(\left( {a;b} \right).\) Mß╗ćnh ─æß╗ü n├Āo sau ─æ├óy sai ?
A. Nß║┐u \(f'\left( x \right) < 0\) vß╗øi mß╗Źi \(x \in \left( {a;b} \right)\) th├¼ h├Ām sß╗æ \(y = f\left( x \right)\) nghß╗ŗch biß║┐n tr├¬n \(\left( {a;b} \right).\)
B. Nß║┐u \(f'\left( x \right) > 0\) vß╗øi mß╗Źi \(x \in \left( {a;b} \right)\) th├¼ h├Ām sß╗æ \(y = f\left( x \right)\) ─æß╗ōng biß║┐n tr├¬n \(\left( {a;b} \right).\)
C. Nß║┐u h├Ām sß╗æ \(y = f\left( x \right)\) nghß╗ŗch biß║┐n tr├¬n \(\left( {a;b} \right)\) th├¼ \(f'\left( x \right) \le 0\) vß╗øi mß╗Źi \(x \in \left( {a;b} \right).\)
D. Nß║┐u h├Ām sß╗æ \(y = f\left( x \right)\) ─æß╗ōng biß║┐n tr├¬n \(\left( {a;b} \right)\) th├¼ \(f'\left( x \right) > 0\) vß╗øi mß╗Źi \(x \in \left( {a;b} \right).\)
C├óu 7: Biß║┐t \(F\left( x \right)\) l├Ā mß╗Öt nguy├¬n h├Ām tr├¬n \(\mathbb{R}\) cß╗¦a h├Ām sß╗æ \(f\left( x \right) = \dfrac{{2017x}}{{{{\left( {{x^2} + 1} \right)}^{2018}}}}\) thß╗Åa m├Żn \(F\left( 1 \right) = 0.\) T├¼m gi├Ī trß╗ŗ nhß╗Å nhß║źt \(m\) cß╗¦a \(F\left( x \right).\)
A. \(m = - \dfrac{1}{2}.\)
B. \(m = \dfrac{{1 - {2^{2017}}}}{{{2^{2018}}}}.\)
C. \(m = \dfrac{{{2^{2017}} + 1}}{{{2^{2018}}}}.\)
D. \(m = \dfrac{1}{2}.\)
C├óu 8: T├Łnh thß╗ā t├Łch \(V\) cß╗¦a khß╗æi n├│n tr├▓n xoay c├│ chiß╗üu cao \(h\) v├Ā ─æ├Īy l├Ā h├¼nh tr├▓n b├Īn k├Łnh \(r.\)
A. \(V = \pi rh.\)
B. \(V = \dfrac{2}{3}\pi rh.\)
C. \(V = \dfrac{1}{3}\pi {r^2}h.\)
D. \(V = \pi {r^2}h.\)
C├óu 9: T├Łch \(2017!.{\left( {1 + \dfrac{1}{1}} \right)^1}{\left( {1 + \dfrac{1}{2}} \right)^2}...{\left( {1 + \dfrac{1}{{2017}}} \right)^{2017}}\) ─æŲ░ß╗Żc viß║┐t dŲ░ß╗øi dß║Īng \({a^b},\) khi ─æ├│ \(\left( {a;b} \right)\) l├Ā cß║Ęp n├Āo trong c├Īc cß║Ęp sau ?
A. \(\left( {2018;2017} \right).\)
B. \(\left( {2019;2018} \right).\)
C. \(\left( {2015;2014} \right).\)
D. \(\left( {2016;2015} \right).\)
C├óu 10: Cho h├Ām sß╗æ \(y = f\left( x \right)\) c├│ ─æß║Īo h├Ām \(f'\left( x \right) = \left( {{x^2} - 1} \right)\left( {x + 1} \right)\left( {5 - x} \right)\).
Mß╗ćnh ─æß╗ü n├Āo sau ─æ├óy ─æ├║ng ?
A. \(f\left( 1 \right) < f\left( 4 \right) < f\left( 2 \right)\).
B. \(f\left( 1 \right) < f\left( 2 \right) < f\left( 4 \right)\).
C. \(f\left( 2 \right) < f\left( 1 \right) < f\left( 4 \right)\).
D. \(f\left( 4 \right) < f\left( 2 \right) < f\left( 1 \right)\).
ĐÁP ÁN
|
1. B |
2. B |
3. B |
4. B |
5. D |
|
6. D |
7. B |
8. C |
9. A |
10. B |
{-- Nß╗Öi dung ─æß╗ü, ─æ├Īp ├Īn tß╗½ c├óu 11-50 c├Īc em vui l├▓ng xem ß╗¤ phß║¦n xem online hoß║Ęc tß║Żi vß╗ü --}
Tr├¬n ─æ├óy l├Ā tr├Łch dß║½n 1 phß║¦n nß╗Öi dung t├Āi liß╗ću Bß╗Ö 4 ─æß╗ü thi thß╗Ł THPT QG n─ām 2021 m├┤n To├Īn - TrŲ░ß╗Øng THPT Triß╗ću SŲĪn. ─Éß╗ā xem to├Ān bß╗Ö nß╗Öi dung c├Īc em ─æ─āng nhß║Łp v├Āo trang hoc247.net ─æß╗ā tß║Żi t├Āi liß╗ću vß╗ü m├Īy t├Łnh.
Hy vß╗Źng t├Āi liß╗ću n├Āy sß║Į gi├║p c├Īc em hß╗Źc sinh ├┤n tß║Łp tß╗æt v├Ā ─æß║Īt th├Ānh t├Łch cao trong hß╗Źc tß║Łp .
C├Īc em quan t├óm c├│ thß╗ā tham khß║Żo th├¬m c├Īc t├Āi liß╗ću c├╣ng chuy├¬n mß╗źc:
-
Bß╗Ö 4 ─æß╗ü thi thß╗Ł THPT QG n─ām 2021 m├┤n To├Īn - TrŲ░ß╗Øng THPT Thanh Thß╗¦y
-
Bß╗Ö 4 ─æß╗ü thi thß╗Ł THPT QG n─ām 2021 m├┤n To├Īn - TrŲ░ß╗Øng THPT Thß╗æng Nhß║źt
-
Bß╗Ö 4 ─æß╗ü thi thß╗Ł THPT QG n─ām 2021 m├┤n To├Īn - TrŲ░ß╗Øng THPT Y├¬n D┼®ng 3
-
Bß╗Ö 4 ─æß╗ü thi thß╗Ł THPT QG n─ām 2021 m├┤n To├Īn - TrŲ░ß╗Øng THPT Ng├┤ Gia Tß╗▒
ŌĆŗCh├║c c├Īc em hß╗Źc tß║Łp tß╗æt !
T├Āi liß╗ću li├¬n quan
TŲ░ liß╗ću nß╗Ģi bß║Łt tuß║¦n
- Xem thêm





.PNG)