Giải bài 26 tr 76 sách GK Toán 9 Tập 2
Cho AB, BC, CA là ba dây của đường tròn (O). Từ điểm chính giữa M của cung AB vẽ dây MN song song với dây BC. Gọi giao điểm của MN và AC là S. Chứng minh \(SM = SC\) và \(SN = SA\)
Hướng dẫn giải chi tiết bài 26
Với bài 26 này, chúng ta sẽ nhắc lại kiến thức về góc nội tiếp chắn cùng một cung hoặc hai cung bằng nhau thì chúng bằng nhau. Hướng dẫn chi tiết giải bài này như sau:
.png)
Theo giả thiết, M là điểm chính giữa của cung AB
\(\Rightarrow sd_{BM}=sd_{AM}\)
Mặc khác, MN song song với BC nên:
\(\Rightarrow sd_{BM}=sd_{NC}\)
\(\Rightarrow sd_{BM}=sd_{NC}=sd_{AM}\)
Vậy các góc nội tiếp chắn ba cung này đều bằng nhau.
\(\Rightarrow \widehat{ANM}=\widehat{NAC}=\frac{\widehat{AOM}}{2}\)
Suy ra tam giác ASN cân tại S
\(\Rightarrow SA=SN\)
Mặc khác:
\(\widehat{SMC}=\widehat{SCM}=\frac{\widehat{CON}}{2}\)
Suy ra tam giác SMN cân tại S
\(\Rightarrow SM=SC\)
-- Mod Toán 9 HỌC247
-


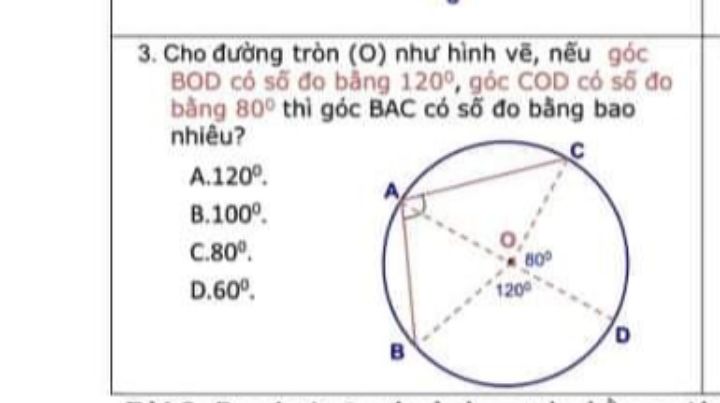
Cho đường tròn (O) như hình vẽ, nếu góc BOD có sđ là 120° , góc COD có sđ là 80° thì góc BAC có sđ là bao nhiêu ?
bởi 白 九 歌
 16/04/2020
16/04/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính quãng đường AB và thời gian dự định đi lúc đầu biết ô tô chạy với vận tốc 35km/h thì đến nơi chậm mất 2 giờ
bởi Phương Thùy
 16/04/2020
16/04/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Cho đường tròn (O) đường kính AB.M là 1điểm trên đường tròn sao cho MAB bằng 30độ.sđ cung MA bằng bao nhiêu ?
bởi Nguyễn Mai
 10/04/2020
10/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 24 trang 76 SGK Toán 9 Tập 2
Bài tập 25 trang 76 SGK Toán 9 Tập 2
Bài tập 15 trang 102 SBT Toán 9 Tập 2
Bài tập 16 trang 102 SBT Toán 9 Tập 2
Bài tập 17 trang 102 SBT Toán 9 Tập 2
Bài tập 18 trang 102 SBT Toán 9 Tập 2
Bài tập 20 trang 102 SBT Toán 9 Tập 2
Bài tập 20 trang 102 SBT Toán 9 Tập 2
Bài tập 21 trang 102 SBT Toán 9 Tập 2
Bài tập 22 trang 102 SBT Toán 9 Tập 2
Bài tập 23 trang 103 SBT Toán 9 Tập 2





