Bài tập 17 tr 102 sách BT Toán lớp 9 Tập 2
Cho đường tròn \((O)\) và hai dây \(AB, AC\) bằng nhau. Qua \(A\) vẽ một cát tuyến cắt dây \(BC\) ở \(D\) và cắt đường tròn \((O)\) ở \(E.\) Chứng minh rằng \(A{B^2} = AD.AE.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Với hai cung nhỏ trong một đường tròn, hai dây bằng nhau căng hai cung bằng nhau.
+) Trong một đường tròn, góc nội tiếp chắn các cung bằng nhau thì bằng nhau.
Lời giải chi tiết
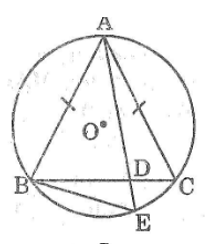
Vì \(AB = AC\;\; (gt)\)
Nên \(\overparen{AB} = \overparen{AC}\) (hai dây bằng nhau căng \(2\) cung bằng nhau)
\( \Rightarrow \widehat {ABC} = \widehat {AEB}\) (\(2\) góc nội tiếp chắn \(2\) cung bằng nhau)
Xét \(∆ABD\) và \(∆ABE:\)
+) \(\widehat A\) chung
+) \(\widehat {ABD}=\widehat {ABC} = \widehat {AEB}\) (chứng minh trên)
Suy ra: \(∆ABD\) đồng dạng \(∆AEB\) (g-g)
\(\Rightarrow \displaystyle {{AE} \over {AB}} = {{AB} \over {AD}}\)\( \Rightarrow {\rm A}{{\rm B}^2} = AD.AE\).
-- Mod Toán 9 HỌC247
-


Cho tam giác ABC nội tiếp (O). Tia phân giác của góc BAC cắt BC tại D và (O) tại E. Chứng minh AB.AC=AE.AD
bởi Châu Lại Lê Hoàng
 13/02/2020
13/02/2020
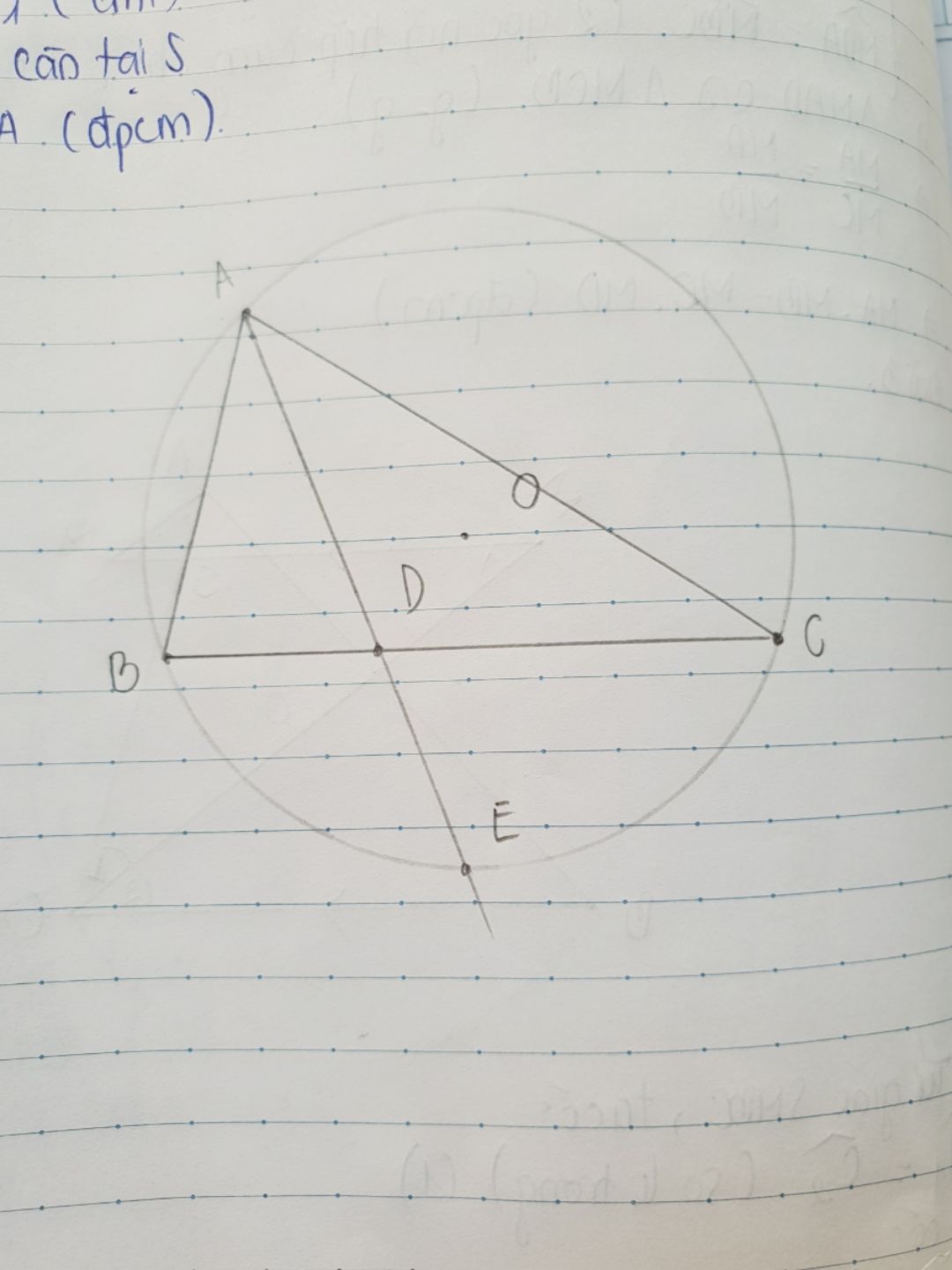 Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


Chứng minh ∆ ABK cân
bởi Vỹ Nguyễn Huỳnh Gia
 10/02/2020
Cho nửa đường tròn (O) đường kính AB, từ A dựng đường thẳng Ax vuông góc với AB ˆ tại A. Gọi C là một điểm trên nửa đường tròn. Tia phân giác của góc CAx cắt nửa đường tròn ở E. AE và BC cắt nhau ở K. a) Chứng minh ∆ ABK cân ? b) GọiIlàgiaođiểmcủaACvàBE.Chứngminh:KI//Ax? c) Chứngminh:OE//BCTheo dõi (0) 1 Trả lời
10/02/2020
Cho nửa đường tròn (O) đường kính AB, từ A dựng đường thẳng Ax vuông góc với AB ˆ tại A. Gọi C là một điểm trên nửa đường tròn. Tia phân giác của góc CAx cắt nửa đường tròn ở E. AE và BC cắt nhau ở K. a) Chứng minh ∆ ABK cân ? b) GọiIlàgiaođiểmcủaACvàBE.Chứngminh:KI//Ax? c) Chứngminh:OE//BCTheo dõi (0) 1 Trả lời -

 Cho tam giác ABC có 3 góc nhọn. Đường tròn tâm O đường kính BC cắt AB ; AC lần lượt tại D và E. a) Chứng minh : CD là đường cao của tam giác ABC ? b) Gọi H là giao điểm của BE và CE.Chứngminh:AH vuông góc BC c) Chứng minh : AD.AB = AE.AC ?Theo dõi (0) 0 Trả lời
Cho tam giác ABC có 3 góc nhọn. Đường tròn tâm O đường kính BC cắt AB ; AC lần lượt tại D và E. a) Chứng minh : CD là đường cao của tam giác ABC ? b) Gọi H là giao điểm của BE và CE.Chứngminh:AH vuông góc BC c) Chứng minh : AD.AB = AE.AC ?Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 15 trang 102 SBT Toán 9 Tập 2
Bài tập 16 trang 102 SBT Toán 9 Tập 2
Bài tập 18 trang 102 SBT Toán 9 Tập 2
Bài tập 20 trang 102 SBT Toán 9 Tập 2
Bài tập 20 trang 102 SBT Toán 9 Tập 2
Bài tập 21 trang 102 SBT Toán 9 Tập 2
Bài tập 22 trang 102 SBT Toán 9 Tập 2
Bài tập 23 trang 103 SBT Toán 9 Tập 2





