Bài tập 23 tr 103 sách BT Toán lớp 9 Tập 2
Cho tam giác cân \(ABC\) \((AB = AC)\) nội tiếp đường tròn tâm \(O.\) Các đường phân giác của hai góc \(B\) và \(C\) cắt nhau ở \(E\) và cắt đường tròn lần lượt ở \(F\) và \(D.\) Chứng minh rằng tứ giác \(EDAF\) là một hình thoi.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong tam giác cân, hai góc kề cạnh đáy bằng nhau.
+) Trong một đường tròn, các góc nội tiếp chắn các cung bằng nhau thì bằng nhau.
+) Tứ giác có các cặp góc song song là hình bình hành.
+) Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
Lời giải chi tiết
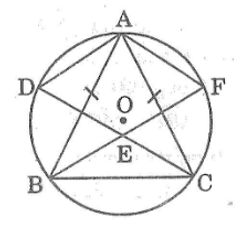
Vì \(∆ABC\) cân tại \(A\)
\( \Rightarrow \widehat {ABC} = \widehat {ACB}\) (tính chất tam giác cân)
Lại có:
\(BF\) là tia phân giác của \(\widehat {ABC}\) \((gt)\)
\(CD\) là tia phân giác của \(\widehat {ACB}\) \((gt)\)
Suy ra: \(\widehat {{B_1}} = \widehat {{B_2}} = \widehat {{C_1}} = \widehat {{C_2}}\)
Suy ra: \(\overparen{AD}\)\(=\overparen{DB}\)\(=\overparen{AF}\)\(=\overparen{FC}\)
Từ đó, đường tròn \((O)\) có: \(\widehat {{A_1}} = \widehat {{B_1}}\) (hai góc nội tiếp chắn \(2\) cung bằng nhau \(BD\) và \(AF\))
\( \Rightarrow AD//BF\) (vì có cặp góc so le trong bằng nhau)
Hay \(AD // EF\;\;\; (1)\)
Tương tự: \(\widehat {{A_2}} = \widehat {{C_1}}\) (hai góc nội tiếp chắn \(2\) cung bằng nhau)
\( \Rightarrow AF // CD\) (vì có cặp góc ở vị trí so le trong bằng nhau)
Hay \(AF // ED \;\;\; (2)\)
Mà \(\overparen{AD}= \overparen{AF}\) (chứng minh trên)
\( \Rightarrow AD = AF\) \( (3)\)
Từ \((1),\) \((2)\) và \((3)\) suy ra: Tứ giác \(ADEF\) là hình thoi
-- Mod Toán 9 HỌC247
-


Bài 21 trang 102 sách bài tập toán 9 tập 2
bởi Ngoc Nga
 10/10/2018
10/10/2018
Bài 21 (Sách bài tập - tập 2 - trang 102)
Cho tam giác ABC nội tiếp đường tròn tâm O, biết \(\widehat{A}=32^0,\widehat{B}=84^0\). Lấy các điểm D, E, F thuộc đường tròn () sao cho AD = AB, BE = BC, CF = CA.
Hãy tính các góc của tam giác DEF ?
Theo dõi (0) 1 Trả lời -


Bài 20 trang 102 sách bài tập toán 9 tập 2
bởi Thùy Nguyễn
 10/10/2018
10/10/2018
Bài 20 (Sách bài tập - tập 2 - trang 102)
Cho tam giác đều ABC nội tiếp đường tròn (O) và M là một điểm của cung nhỏ BC. Trên MA lấy điểm D sao cho MD = MB.
a) Hỏi tam giác MBD là tam giác gì ?
b) So sánh tam giác BDA và BMC
c) Chứng minh rằng MA = MB + MC
Theo dõi (0) 1 Trả lời -


Bài 19 trang 102 sách bài tập toán 9 tập 2
bởi Nguyễn Minh Hải
 10/10/2018
10/10/2018
Bài 19 (Sách bài tập - tập 2 - trang 102)
Để giúp xe lửa chuyển từ một đường ray từ hướng này sang một đường ray hướng khác, người ta làm xen giữa một đoạn đường ray hình vòng cung (h.1). Biết chiều rộng của đường ray là \(AB\approx1,1m\), đoạn \(BC\approx28,4m\). Hãy tính bán kính OA = R của đoạn đường ray hình vòng cung ?
Theo dõi (0) 1 Trả lời





