Giải bài 24 tr 76 sách GK Toán 9 Tập 2
Một chiếc cầu được thiết kế như hình 21 có độ dài \(AB = 40m\), chiều cao \(MK = 3m\). Hãy tính bán kính của đường tròn chứa cung AMB
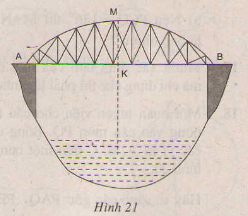
Hướng dẫn giải chi tiết bài 24
Chúng ta sẽ mô phỏng lại bài 24 bằng hình vẽ sau, và tính bán kính của đường tròn.
.png)
Dựng đường kính MN của đường tròn (O).
Góc MAN là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow \widehat{MAN}=90^o\)
Dễ dàng chứng minh được MN là đường trung trực của AB
\(\Rightarrow AH=HB=\frac{AB}{2}\)
Áp dụng định lí Pytago vào tam giác AHM vuông tại H:
\(AM=\sqrt{AH^2+MH^2}=\sqrt{20^2+3^2}=\sqrt{409}(m)\)
Mặc khác, theo hệ thức lượng trong tam giác AMN vuông tại A có đường cao AH:
\(AM^2=MH.MN\Rightarrow MN=\frac{AM^2}{MH}=\frac{409}{3}\)
\(\Rightarrow R=\frac{409}{6}\approx 68,17(m)\)
-- Mod Toán 9 HỌC247
-


Chứng minh tứ giác ADMC nội tiếp?
bởi Anh Lan
 15/05/2020
15/05/2020
Giúp mình câu c với mn
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh góc HCB bằng góc CAB?
bởi Van Hanhdao
 22/04/2020
cm hai góc bằng nhau
22/04/2020
cm hai góc bằng nhau Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Số đo góc DBE là?
bởi Pin Su
 22/04/2020
22/04/2020
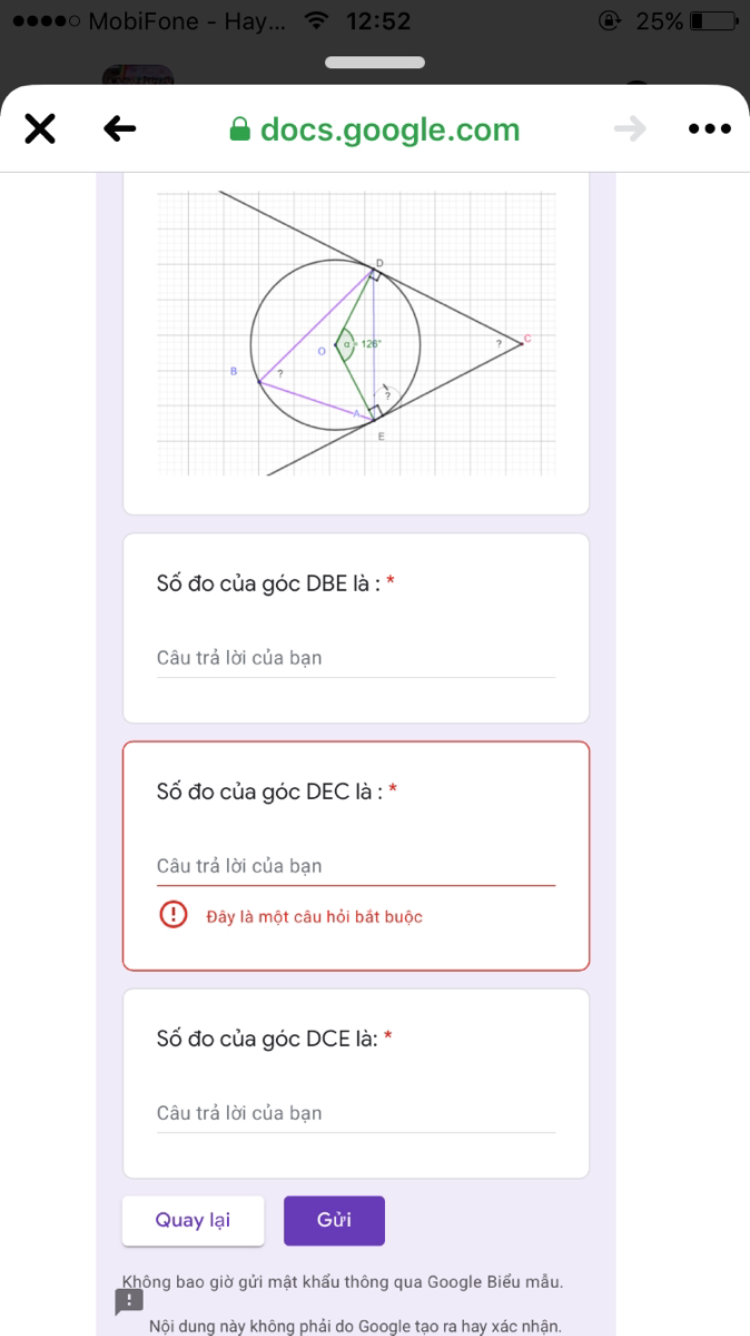 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 22 trang 76 SGK Toán 9 Tập 2
Bài tập 23 trang 76 SGK Toán 9 Tập 2
Bài tập 25 trang 76 SGK Toán 9 Tập 2
Bài tập 26 trang 76 SGK Toán 9 Tập 2
Bài tập 15 trang 102 SBT Toán 9 Tập 2
Bài tập 16 trang 102 SBT Toán 9 Tập 2
Bài tập 17 trang 102 SBT Toán 9 Tập 2
Bài tập 18 trang 102 SBT Toán 9 Tập 2
Bài tập 20 trang 102 SBT Toán 9 Tập 2
Bài tập 20 trang 102 SBT Toán 9 Tập 2
Bài tập 21 trang 102 SBT Toán 9 Tập 2
Bài tập 22 trang 102 SBT Toán 9 Tập 2
Bài tập 23 trang 103 SBT Toán 9 Tập 2





