Bài tập 18 tr 102 sách BT Toán lớp 9 Tập 2
Cho đường tròn \((O)\) và một điểm \(M\) cố định không nằm trên đường tròn. Qua \(M\) vẽ một cát tuyến bất kì cắt đường tròn ở \(A\) và \(B.\) Chứng minh rằng tích \(MA.MB\) không đổi.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải chi tiết
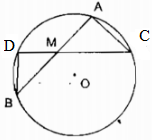
Trường hợp M ở bên trong đường tròn (O)
Kẻ cát tuyến AB bất kỳ và kẻ đường thẳng MO cắt đường tròn tại C và D.
Xét hai ∆MAC và ∆MBD:
\(\widehat {AMC} = \widehat {BMD}\) (đối đỉnh)
\(\widehat A = \widehat D\) (hai góc nội tiếp cùng chắn cung \(\overparen{BC}\)
Suy ra: ∆MAC đồng dạng ∆MDB (g.g)
\( \Rightarrow {{MB} \over {MC}} = {{MD} \over {MA}}\)
\( \Rightarrow MA.MB = MC.MD\) (1)
Vì M, O cố định suy ra điểm C và D cố định nên độ dài của các đoạn MC và MD không đổi \( \Rightarrow \) tích MC.MD không đổi (2)
Từ (1) và (2) suy ra tích MA. MB không đổi khi cát tuyến AB thay đổi.
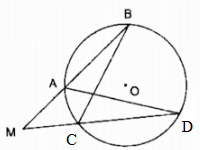
Trường hợp điểm M ở ngoài đường tròn (O)
Kẻ cát tuyến MAB bất kỳ của (O) và đường thẳng MO cắt đường tròn (O) tại C và D
Xét ∆MAD và ∆MCB:
\(\widehat M\) chung
\(\widehat B = \widehat D\) (hai góc nội tiếp cùng chắn cung \(\overparen{AC}\))
Suy ra: ∆MAD đồng dạng ∆MCB (g.g)
\( \Rightarrow {{MC} \over {MA}} = {{MB} \over {MD}} \Rightarrow MA.MB = MC.MD\) (3)
Vì M và O cố định suy ra điểm C, D cố định nên độ dài của các đoạn MC và MD không đổi \( \Rightarrow \) tích MC. MD không đổi (4)
Từ (3) và (4) suy ra tích MA. MB không đổi khi cát tuyến MAB thay đổi.
-- Mod Toán 9 HỌC247
-


Cho hình bình hành ABCD, góc A bé hơn 90độ đường tròn ngoại tiếp tam giác BCD cắt AC ở E. Chứng minh rằng BD là tiếp tuyến của đường tròn ngoại tiếp tam giác AEB
Theo dõi (0) 2 Trả lời -


Tính giá trị biểu thức A khi x=1/4
bởi Khánh Huyền
 05/02/2020
05/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh MA.MB= MC.MD = MO^2 - R^2 biết A nằm giữa M và B, C nằm giữa M và D
bởi Ánh Ngọc
 29/01/2020
Giúp mình với. Mình cần gấp. Cảm ơnTheo dõi (0) 0 Trả lời
29/01/2020
Giúp mình với. Mình cần gấp. Cảm ơnTheo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 16 trang 102 SBT Toán 9 Tập 2
Bài tập 17 trang 102 SBT Toán 9 Tập 2
Bài tập 20 trang 102 SBT Toán 9 Tập 2
Bài tập 20 trang 102 SBT Toán 9 Tập 2
Bài tập 21 trang 102 SBT Toán 9 Tập 2
Bài tập 22 trang 102 SBT Toán 9 Tập 2
Bài tập 23 trang 103 SBT Toán 9 Tập 2





