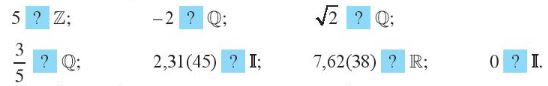Giải bài 1 trang 38 SGK Toán 7 Chân trời sáng tạo tập 1
Hãy thay mỗi ? bằng kí hiệu \( \in \) hoặc \( \notin \) để có phát biểu đúng.
Hướng dẫn giải chi tiết Giải bài 1 trang 38
Phương pháp giải
\(\mathbb{Z} = \left\{ {...; - 2; - 1;0;1;2;...} \right\}\)
\(\mathbb{Q} = \left\{ {\frac{a}{b};\,a,b \in \mathbb{Z};\,b \ne 0} \right\}\)
Mỗi số thập phân vô hạn không tuần hoàn là biểu diễn thập phân của một số, số đó gọi là số vô tỉ. Kí hiệu là I.
Tập hợp số hữu tỉ \(\mathbb{R}\) bao gồm các số vô tỉ và hữu tỉ.
Lời giải chi tiết
\(\begin{array}{l}5 \in \mathbb{Z};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 2 \in \mathbb{Q};\,\,\,\,\,\,\,\,\,\,\,\,\,\sqrt 2 \notin \mathbb{Q};\\\frac{3}{5} \in \mathbb{Q};\,\,\,\,\,\,\,\,\,\,\,\,2,31\left( {45} \right) \notin I\,\,\,\,\,\,7,62\left( {38} \right) \in \mathbb{R};\,\,\,\,0 \notin I\end{array}\)
-- Mod Toán 7 HỌC247
-


Tìm: \(\left| { - {\rm{ }}2{\rm{ }}022} \right|;{\rm{ }}\left| {\sqrt {312} } \right|;{\rm{ }}\left| { - \sqrt {5,4} } \right|;{\rm{ }}\left| {\dfrac{{ - 273}}{3}} \right|;{\rm{ }}\left| { - 20,21} \right|\).
bởi hi hi
 25/11/2022
Theo dõi (0) 1 Trả lời
25/11/2022
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Thực hành 5 trang 37 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Vận dụng 4 trang 37 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 38 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 38 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 38 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 38 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 38 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 38 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 38 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 38 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 40 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 40 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 40 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 41 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 41 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 41 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 41 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 41 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 41 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 41 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 11 trang 41 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST