Phß║¦n hŲ░ß╗øng dß║½n giß║Żi b├Āi tß║Łp SGK To├Īn 7 B├Āi 3 ─Éß║Īi lŲ░ß╗Żng tß╗ē lß╗ć nghß╗ŗch sß║Į gi├║p c├Īc em nß║»m ─æŲ░ß╗Żc phŲ░ŲĪng ph├Īp v├Ā r├©n luyß╗ćn k─® n─āng c├Īc dß║Īng b├Āi tß║Łp tß╗½ SGK To├Īn 7 Tß║Łp mß╗Öt.
-
B├Āi tß║Łp 12 trang 58 SGK To├Īn 7 Tß║Łp 1
Cho biß║┐t hai ─æß║Īi lŲ░ß╗Żng x v├Ā y tß╗ē lß╗ć nghß╗ŗch vß╗øi nhau v├Ā khi x = 8 th├¼ y = 15
a) T├¼m hß╗ć sß╗æ tß╗ē lß╗ć.
b) H├Ży biß╗āu diß║┐n y theo x.
c) T├Łnh gi├Ī trß╗ŗ cß╗¦a y khi x =6; y = 10.
-
B├Āi tß║Łp 13 trang 58 SGK To├Īn 7 Tß║Łp 1
Cho biß║┐t x v├Ā y l├Ā hai ─æß║Īi lŲ░ß╗Żng tß╗ē lß╗ć nghß╗ŗch. ─Éiß╗ün sß╗æ th├Łch hß╗Żp v├Āo ├┤ trß╗æng trong bß║Żng sau:
x
0,5
-1,2
4
6
y
3
-2
1,5
-
B├Āi tß║Łp 14 trang 58 SGK To├Īn 7 Tß║Łp 1
Cho biß║┐t 35 c├┤ng nh├Żn├óy mß╗Öt ng├┤i nh├Ā hß║┐t 168 ng├Āy. Hß╗Åi 28 c├┤ng nh├ón x├óy ng├┤i nh├Ā ─æ├│ hß║┐t bao nhi├¬u ng├Āy? (Giß║Ż sß╗Ł n─āng suß║źt cß╗¦a mß╗Śi c├┤ng nhan l├Ā nhŲ░ nhau).
-
B├Āi tß║Łp 15 trang 58 SGK To├Īn 7 Tß║Łp 1
a) Cho biß║┐t ─æß╗Öi A d├╣ng x m├Īy c├Āy (c├│ c├╣ng n─āng suß║źt) ─æß╗ā c├Āy xong mß╗Öt c├Īnh ─æß╗ōng hß║┐t y giß╗Ø. Hai ─æß║Īi lŲ░ß╗Żng x v├Ā y c├│ tß╗ē lß╗ć nghß╗ŗch vß╗øi nhau kh├┤ng?
b) Cho biß║┐t x l├Ā sß╗æ trang ─æ├Ż ─æß╗Źc xong v├Ā y l├Ā sß╗æ trang cong lß║Īi chŲ░a ─æß╗Źc cß╗¦a mß╗Öt quyß╗ān s├Īch. Hß╗Åi x v├Ā y c├│ phß║Żi l├Ā hai ─æß║Īi lŲ░ß╗Żng tß╗ē lß╗ć nghß╗ŗch kh├┤ng?
c) Cho biß║┐t a(m) l├Ā chu vi cß╗¦a b├Īnh xe, b l├Ā sß╗æ v├▓ng quay ─æŲ░ß╗Żc cß╗¦a b├Īnh xe tr├¬n ─æoß║Īn ─æŲ░ß╗Øng xe l─ān tß╗½ A ─æß║┐n B. Hß╗Åi a v├Ā b c├│ phß║Żi l├Ā hai ─æß║Īi lŲ░ß╗Żng tß╗ē lß╗ć nghß╗ŗch kh├┤ng?
-
B├Āi tß║Łp 18 trang 68 SBT To├Īn 7 Tß║Łp 1
Cho biß║┐t \(x\) v├Ā \(y\) l├Ā hai ─æß║Īi lŲ░ß╗Żng tß╗ē lß╗ć nghß╗ŗch.
a) Thay c├Īc dß║źu "?" bß║▒ng c├Īc sß╗æ th├Łch hß╗Żp trong bß║Żng dŲ░ß╗øi ─æ├óy.
x
x┬Ł1 = 2
x2 = 3
x3 = 5
x4 = 6
y
y1 = 15
y2 = ?
y3 = ?
y4 = ?
xy
x1y1 = ?
x2y2 = ?
x3y3 = ?
x4y4 = ?
b) C├│ nhß║Łn x├®t g├¼ vß╗ü t├Łch c├Īc gi├Ī trß╗ŗ tŲ░ŲĪng ß╗®ng cß╗¦a \(x\) v├Ā \(y\) \(({x_1}{y_1},{x_2}{y_2},{x_3}{y_3},{x_4}{y_4})?\)
-
B├Āi tß║Łp 19 trang 68 SBT To├Īn 7 Tß║Łp 1
Cho biß║┐t \(x\) v├Ā \(y\) l├Ā hai ─æß║Īi lŲ░ß╗Żng tß╗ē lß╗ć nghß╗ŗch v├Ā khi \(x = 7\) th├¼ \(y =10\).
a) H├Ży t├¼m hß╗ć sß╗æ tß╗ē lß╗ć nghß╗ŗch cß╗¦a \(y\) ─æß╗æi vß╗øi \(x\).
b) H├Ży biß╗āu diß╗ģn \(y\) theo \(x\).
c) T├Łnh gi├Ī trß╗ŗ cß╗¦a \(y\) khi \(x = 5; x = 14\).
-
B├Āi tß║Łp 20 trang 68 SBT To├Īn 7 Tß║Łp 1
Cho biß║┐t \(x\) v├Ā \(y\) l├Ā hai ─æß║Īi lŲ░ß╗Żng tß╗ē lß╗ć nghß╗ŗch. ─Éiß╗ün c├Īc sß╗æ th├Łch hß╗Żp v├Āo c├Īc ├┤ trß╗æng trong bß║Żng sau:
x
1
2,5
8
10
y
-4
-2,5
-2
-
B├Āi tß║Łp 21 trang 69 SBT To├Īn 7 Tß║Łp 1
Cho biß║┐t ba m├Īy c├Āy, c├Āy xong mß╗Öt c├Īnh ─æß╗ōng hß║┐t \(30\) giß╗Ø. Hß╗Åi n─ām m├Īy c├Āy nhŲ░ thß║┐ (c├╣ng n─āng suß║źt) c├Āy xong c├Īnh ─æß╗ōng ─æ├│ hß║┐t bao nhi├¬u giß╗Ø?
-
B├Āi tß║Łp 22 trang 69 SBT To├Īn 7 Tß║Łp 1
Mß╗Öt ├┤ t├┤ chß║Īy tß╗½ A ─æß║┐n B vß╗øi vß║Łn tß╗æc \(45km/h\) hß║┐t \(3\) giß╗Ø \(15\) ph├║t. Hß╗Åi chiß║┐c ├┤ t├┤ ─æ├│ chß║Īy tß╗½ A ─æß║┐n B vß╗øi vß║Łn tß╗æc \(65km/h\) sß║Į h├¬╠üt bao nhi├¬u thß╗Øi gian?
-
B├Āi tß║Łp 23 trang 69 SBT To├Īn 7 Tß║Łp 1
Cho biß║┐t \(56\) c├┤ng nh├ón ho├Ān th├Ānh mß╗Öt c├┤ng viß╗ćc trong \(21\) ng├Āy. Hß╗Åi cß║¦n phß║Żi t─āng th├¬m bao nhi├¬u c├┤ng nh├ón nß╗»a ─æß╗ā c├│ thß╗ā ho├Ān th├Ānh c├┤ng viß╗ćc ─æ├│ trong \(14\) ng├Āy? (N─āng suß║źt cß╗¦a c├Īc c├┤ng nh├ón l├Ā nhŲ░ nhau).
-
B├Āi tß║Łp 24 trang 69 SBT To├Īn 7 Tß║Łp 1
─Éß╗æ: Mß╗Öt thß╗Åi v├Āng h├¼nh hß╗Öp chß╗» nhß║Łt (h├¼nh dŲ░ŲĪ╠üi) c├│ chiß╗üu d├Āi 5cm, mß║Ęt cß║»t ngang (─æ├Īy) l├Ā mß╗Öt h├¼nh vu├┤ng cß║Īnh 1cm. Tß╗½ thß╗Åi v├Āng ─æ├│ ngŲ░ß╗Øi ta l├Ām th├Ānh mß╗Öt d├óy v├Āng c┼®ng h├¼nh hß╗Öp chß╗» nhß║Łt. ─Éß╗æ em biß║┐t chiß╗üu d├Āi cß╗¦a d├óy v├Āng ─æ├│ bß║▒ng bao nhi├¬u nß║┐u mß║Ęt cß║»t ngang cu╠ēa n├│ l├Ā h├¼nh vu├┤ng cß║Īnh 1mm?
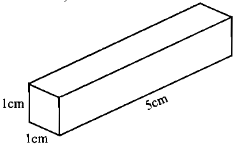
-
B├Āi tß║Łp 3.1 trang 69 SBT To├Īn 7 Tß║Łp 1
T├¼m lß╗Śi. Cho \(x\) tß╗ē lß╗ć nghß╗ŗch vß╗øi \(y\) v├Ā \(y\) tß╗ē lß╗ć nghß╗ŗch vß╗øi \( z\). H├Ży cho biß║┐t mß╗æi quan hß╗ć giß╗»a \(x\) v├Ā \(z.\) H├Ży nhß║Łn x├®t hai trß║Ż lß╗Øi sau ─æ├óy cß╗¦a hai bß║Īn.
B├Āi giß║Żi cß╗¦a bß║Īn H├╣ng:
\(\left\{ \begin{array}{l}
x = \dfrac{y}{a}\left( {a \ne 0} \right)\\
y = \dfrac{z}{b}\left( {b \ne 0} \right)
\end{array} \right.\)\(\, \Rightarrow x = \dfrac{z}{b}:a = \dfrac{z}{{ab}}\left( {ba \ne 0} \right)\)Vß║Ły \(x\) tß╗ē lß╗ć nghß╗ŗch vß╗øi \(z\) theo hß╗ć sß╗æ tß╗ē lß╗ć \(b.a\).
B├Āi giß║Żi cß╗¦a bß║Īn Hoa
\(\left\{ \begin{array}{l}
x = \dfrac{a}{y}\left( {a \ne 0} \right)\\
y = \dfrac{b}{z}\left( {b \ne 0} \right)
\end{array} \right.\)\(\, \Rightarrow x = \dfrac{a}{{\dfrac{b}{z}}} = \dfrac{{a.z}}{b} = \dfrac{a}{b}.z\left( {\dfrac{a}{b} \ne 0} \right)\)Vß║Ły \(x\) tß╗ē lß╗ć thuß║Łn vß╗øi \(z\) theo hß╗ć sß╗æ tß╗ē lß╗ć \(\dfrac{a}{b}.\)
-
B├Āi tß║Łp 3.2 trang 69 SBT To├Īn 7 Tß║Łp 1
Cho biß║┐t hai ─æß║Īi lŲ░ß╗Żng \(x\) v├Ā \(y\) tß╗ē lß╗ć nghß╗ŗch vß╗øi nhau v├Ā khi \(x = 6\) th├¼ \(y = -5.\) Khi ─æ├│, biß╗āu diß╗ģn \(y\) theo \(x\) ta ─æŲ░ß╗Żc :
(A) \(y = - \dfrac{{30}}{x}\);
(B) \(y = -30x\);
(C) \(y = \dfrac{{ - 5}}{{6x}}\);
(D) \(y = - \dfrac{5}{6}x\).






