Phần hướng dẫn giải bài tập SGK Toán 7 Bài 11 Số vô tỉ - Khái niệm căn bậc hai sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 7 Tập một.
-
Bài tập 82 trang 41 SGK Toán 7 Tập 1
Theo mẫu:
Vì \(2^{2}=4\) nên
hãy hoàn thành bài tập sau:
a) Vì \(5^{2}=...\) nên
b) Vì \(7^{...}=49\) nên \(...=7\);
c) Vì \(1^{...}=1\) nên
d) Vì \(\left ( \frac{2}{3} \right )^{2}=...\) nên \(...=....\).
-
Bài tập 83 trang 41 SGK Toán 7 Tập 1
Ta có \(\sqrt{25}=5; -\sqrt{25}=-5; \sqrt{(-5)^{2}}=\sqrt{25}=5.\)
Theo mẫu trên, hãy tính:
a)
;
b)
;
c)
d)
e)
-
Bài tập 84 trang 41 SGK Toán 7 Tập 1
Nếu
thì \(x^{2}\) bằng:
A) 2;
B) 4;
C) 8;
D) 16.
Hãy chọn câu trả lời đúng.
-
Bài tập 85 trang 42 SGK Toán 7 Tập 1
Điền số thích hợp vào ô trống

-
Bài tập 86 trang 42 SGK Toán 7 Tập 1
Sử dụng máy tính bỏ túi.
Nút dấu căn bậc hai:


Dùng máy tính bỏ túi để tính:
\(\sqrt{3783025};\sqrt{1125,45}; \sqrt{\frac{0,3+1,2}{0,7}};\frac{\sqrt{6,4}}{1,2}.\)
-
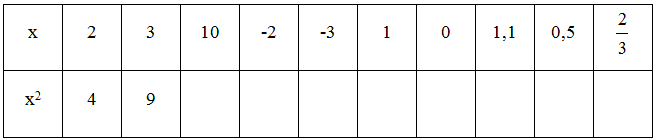
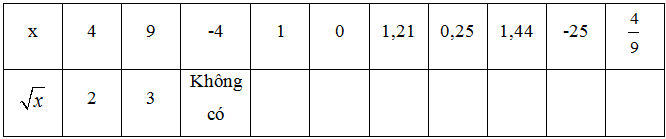
Bài tập 106 trang 27 SBT Toán 7 Tập 1
Điền số thích hợp vào các bảng sau:
-
Bài tập 107 trang 28 SBT Toán 7 Tập 1
Tính:
a) \(\sqrt {81} \)
b) \(\sqrt {8100} \)
c) \(\sqrt {64} \)
d) \(\sqrt {0,64} \)
e) \({\rm{}}\sqrt {1000000} \)
g) \(\sqrt {0,01} \)
h) \(\displaystyle \sqrt {{{49} \over {100}}} \)
i) \(\sqrt {\displaystyle {4 \over {25}}} \)
k) \(\displaystyle \sqrt {{{0,09} \over {121}}} \)
-
Bài tập 108 trang 28 SBT Toán 7 Tập 1
Trong các số sau đây, số nào có căn bậc hai? Hãy cho biết căn bậc hai không âm của các số đó:
\(a = 0\) \(b = -25\)
\(c = 1\) \(d = 16 + 9\)
\({\rm{e}} = {3^2} + {4^2}\) \(g = \pi - 4\)
\(h = {(2 - 11)^2}\) \(i = {\left( { - 5} \right)^2}\)
\(k = - {3^2}\) \(l= \sqrt {16} \)
\(m = {3^4}\) \(n = {5^2} - {3^2}\)
-
Bài tập 109 trang 28 SBT Toán 7 Tập 1
Hãy cho biết mỗi số sau đây là căn bậc hai của số nào?
\(a{\rm{ }} = {\rm{ }}2{\rm{ }};{\rm{ }}b{\rm{ }} = {\rm{ }} - 5{\rm{ }};{\rm{ }}c{\rm{ }} = {\rm{ }}1{\rm{ }};{\rm{ }}d{\rm{ }} = {\rm{ }}25{\rm{ }};\)
\({\rm{ }}e{\rm{ }} = {\rm{ }}0{\rm{ }};{\rm{ }}g{\rm{ }} = \sqrt 7 \)
\(\displaystyle h = {3 \over 4};i = \sqrt 4 - 3;k = {1 \over 4} - {1 \over 2}\)
-
Bài tập 110 trang 28 SBT Toán 7 Tập 1
Tìm căn bậc hai không âm của các số sau:
a) \({\rm{}}16;1600;0,16;{16^2}\)
b) \(25;{5^2};{\left( { - 5} \right)^2};{25^2}\)
c) \(1 ;100 ;0,01 ;10000\)
d) \(0,04 ;0,36 ;1,44 ;0,0121\).
-
Bài tập 111 trang 28 SBT Toán 7 Tập 1
Trong các số sau, số nào bằng \(\displaystyle {3 \over 7}\)?
\(\displaystyle a= {{39} \over {91}}\)
\(\displaystyle b = \sqrt {{{{3^2}} \over {{7^2}}}} \)
\(\displaystyle c = {{\sqrt {{3^2}} + \sqrt {{{39}^2}} } \over {\sqrt {{7^2}} + \sqrt {{{91}^2}} }}\)
\(\displaystyle d= {{\sqrt {{3^2}} - \sqrt {{{39}^2}} } \over {\sqrt {{7^2}} - \sqrt {{{91}^2}} }}\)
-
Bài tập 112 trang 29 SBT Toán 7 Tập 1
Trong các số sau, số nào không bằng \(2,4 \)?
\(a = \sqrt {{{\left( {2,5} \right)}^2} - {{\left( {0,7} \right)}^2}} \)
\(b = \sqrt {{{\left( {2,5 - 0,7} \right)}^2}} \)
\(c = \sqrt {\left( {2,5 + 0,7} \right)\left( {2,5 - 0,7} \right)} \)
\(d = \sqrt {5,76} \)
\(e = \sqrt {1,8.3,2} \)
\(g = 2,5 - 0,7\)
-
Bài tập 113 trang 29 SBT Toán 7 Tập 1
a) Điền số thích hợp vào chỗ trống (…)
\(\eqalign{
& \sqrt {121} = ... \cr
& \sqrt {12321} = ... \cr
& \sqrt {1234321} = ... \cr} \)b) Viết tiếp ba đẳng thức nữa vào ''danh sách'' trên.
-
Bài tập 114 trang 29 SBT Toán 7 Tập 1
a) Điền số thích hợp vào chỗ trống (…):
\(\sqrt 1 = ...\)
\(\sqrt {1 + 2 + 1} = ...\)
\(\sqrt {1 + 2 + 3 + 2 + 1} = ...\)
b) Viết tiếp ba đẳng thức nữa vào "danh sách" trên.
-
Bài tập 115 trang 29 SBT Toán 7 Tập 1
Cho \(x\) là số hữu tỉ khác \(0,\) \(y\) là một số vô tỉ. Chứng tỏ rằng \(x + y\) và \(x.y\) là những số vô tỉ .
-
Bài tập 116 trang 29 SBT Toán 7 Tập 1
Biết \(a\) là số vô tỉ. Hỏi \(b\) là số hữu tỉ hay vô tỉ nếu:
a) \(a + b\) là số hữu tỉ?
b) \(a.b\) là số hữu tỉ?
-
Bài tập 11.1 trang 29 SBT Toán 7 Tập 1
Trong các số \(\sqrt {289} ; - \displaystyle {1 \over {11}}; 0,131313...;\)\( 0,010010001...,\) số vô tỉ là số:
(A) \(\sqrt {289} ;\)
(B) \(\displaystyle - {1 \over {11}}\);
(C) \(0,131313...;\)
(D) \(0,010010001...\)
Hãy chọn đáp án đúng.
-
Bài tập 11.2 trang 29 SBT Toán 7 Tập 1
\(\sqrt {256} \) bằng:
(A) \(128 ;\) (B) \(-128 ;\)
(C) \(16;\) (D) \(±16.\)
Hãy chọn đáp án đúng.
-
Bài tập 11.3 trang 30 SBT Toán 7 Tập 1
Không dùng bảng số hoặc máy tính, hãy so sánh:
\(\sqrt {40 + 2} \) với \(\sqrt {40} + \sqrt 2 \)
-
Bài tập 11.4 trang 30 SBT Toán 7 Tập 1
Cho \(A =\displaystyle \sqrt {625} - {1 \over {\sqrt 5 }};\)
\(\displaystyle B = \sqrt {576} - {1 \over {\sqrt 6 }} + 1\)
Hãy so sánh \(A\) và \(B\).
-
Bài tập 11.5 trang 30 SBT Toán 7 Tập 1
Cho \(A = \sqrt {x + 2} + \displaystyle {3 \over {11}};\)
\(B =\displaystyle {5 \over {17}} - 3\sqrt {x - 5} \)
a) Tìm giá trị nhỏ nhất của A.
b) Tìm giá trị lớn nhất của B.
-
Bài tập 11.6 trang 30 SBT Toán 7 Tập 1
Cho \(\displaystyle A = {{\sqrt x - 3} \over 2}\). Tìm \(x ∈\mathbb Z\) và \(x < 30\) để \(A\) có giá trị nguyên.
-
Bài tập 11.7 trang 30 SBT Toán 7 Tập 1
Cho \(\displaystyle B = {5 \over {\sqrt x - 1}}\). Tìm \(x ∈\mathbb Z\) để \(B\) có giá trị nguyên.






