Giải bài 43 tr 112 sách BT Toán lớp 7 Tập 1
Hãy chứng minh định lí:
Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau.
Hướng dẫn: Chứng minh tương tự bài tập 30.
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Tiên đề Ơclit: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
- Nếu đường thẳng \(c\) cắt hai đường thẳng \(a, b\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc cặp góc đồng vị bằng nhau, hoặc cặp góc trong cùng phía bù nhau) thì \(a\) và \(b\) song song với nhau.
Lời giải chi tiết
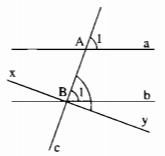
Chứng minh:
Giả sử \(\widehat {{A_1}} \ne \widehat {{B_1}}\).
Qua B kẻ đường thẳng xy tạo với đường thẳng c có \(\widehat {ABy} = \widehat {{A_1}}\).
Theo dấu hiệu của hai đường thẳng song song, ta có xy // a.
Vì xy và a tạo ra với đường thẳng c cắt chúng hai góc đồng vị bằng nhau.
Như vậy qua điểm B ở ngoài đường thẳng a kẻ được 2 đường thẳng b và xy cùng song song với a. Theo tiên đề Ơclít thì đường thẳng xy trùng với đường thẳng b. Vậy \(\widehat {ABy}\) trùng với \(\widehat {{B_1}}\) nên \(\widehat {{A_1}} = \widehat {{B_1}}\)
-- Mod Toán 7 HỌC247
-
Chứng minh định lí 2 tia phân giác của 2 góc kề bù vuông góc với nhau
bởi Phạm Hoàng Thị Trà Giang
09/04/2019
cm định lý 2 tia p/g của â góc kề bù vuông góc vs nhau
Theo dõi (0) 1 Trả lời -
Chứng minh định lí Hai tia phân giác của hai góc kề bù tạo thành 1 góc vuông
bởi Nguyễn Lê Thảo Trang
10/04/2019
Chứng minh các định lí sau: (vẽ hình, nêu GT và KL, chứng minh)
a, Hai tia phân giác của hai góc kề bù tạo thành 1 góc vuông
b, Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ 3 thì chúng song song với nhau
c, Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ 3 thì chúng song song với nhau
Theo dõi (0) 1 Trả lời -
Nếu hai đường thẳng a, b cắt đường thẳng c mà trong các góc tạo thành có một cặp góc... ?
bởi thu hằng
10/04/2019
Nếu hai đường thẳng a , b cắt đường thẳng c mà trong các góc tạo thành có một cặp góc trong cùng phía bù nhau thì a//b. M.n cho mình hỏi đúng hay sai ạ ?
Theo dõi (0) 2 Trả lời -
Chứng minh định lí Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong các góc tạo thành
bởi Nguyễn Sơn Ca
10/04/2019
Cho định lí : Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì các góc đồng vị bằng nhau.
- Hãy cho biết giả thiết của định lí đó.
- Hãy cho biết kết luận của định lí đó.
- Hãy chứng minh định lí đó.
Theo dõi (0) 2 Trả lời -
Tính giá trị biểu thức N = a^3 + a^2b - ab - b^2 -2a^2 + a + 3b + 2015 biết a + b - 2 = 0
bởi Phan Quân
16/01/2019
Tính giá trị biểu thức sau: N = a3 + a2b - ab - b2 - 2a2 + a + 3b + 2015, biết a + b - 2 = 0
Theo dõi (0) 2 Trả lời -
Phát triển các định lý được diễn tả bằng hình vẽ sau và viết giả thiết và kết luận
bởi Phan Quân
11/04/2019
Hãy phát triển các định lý được diễn tả bằng hình vẽ sau và viết giả thiết và kết luận
Theo dõi (0) 1 Trả lời -
Chứng minh định lí Nếu một tâm giác có một đường trung tuyến đồng thời là đường phân giác
bởi Nguyễn Thị Thúy
16/04/2019
chúng minh định lí: nếu một tâm giác có một đường trung tuyến đồng thời là đường ohân giác thì tâm giác đó làm tam giác cân
Theo dõi (0) 2 Trả lời
