Giải bài 41 tr 112 sách BT Toán lớp 7 Tập 1
Với hai góc kề bù, ta có định lí sau:
Hai tia phân giác của hai góc kề bù tạo thành một góc vuông.
a) Hãy vẽ hai góc \(xOy\) và \(yOx'\) kề bù, tia phân giác \(Ot\) của góc \(xOy\), tia phân giác \(Ot'\) của góc \(yOx'\) và gọi số đo của góc \(xOy\) là \(m^\circ \).
b) Hãy viết giả thiết và kết luận của định lí.
c) Hãy điền vào chỗ trống (…) và sắp xếp bốn câu sau đây một cách hợp lý để chứng minh định lí trên:
\(1.\widehat {tOy} = \displaystyle {1 \over 2}m^\circ \) vì ……
\(2.\widehat {t'Oy} = \displaystyle {1 \over 2}(180^\circ - m^\circ )\) vì ……
\(3.\widehat {tOt'} = 90^\circ \) vì ……
\(4.\widehat {x'Oy} = 180^\circ - m^\circ \) vì ……
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Một tính chất được khẳng định là đúng bằng suy luận được gọi là định lí.
- Định lí thường phát biểu dưới dạng: " Nếu \(A\) thì \(B\)" với \(A\) là giả thiết, là điều kiện cho biết; \(B\) là kết luận, là điều được suy ra.
- Tổng số đo hai góc kề bù bằng \(180^o\).
Lời giải chi tiết
a) Hình vẽ:
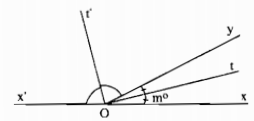
b)
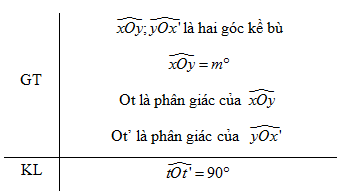
c) \(\widehat {x'Oy} = 180^\circ - m^\circ \) (Vì \(\widehat {x'Oy}\) và \(\widehat {{\rm{yOx}}}\) kề bù)
\(\widehat {tOy} = {1 \over 2}m^\circ \) (Vì Ot là tia phân giác của \(\widehat {x'Oy}\))
\(\widehat {t'Oy} = {1 \over 2}\left( {180^\circ - m^\circ } \right)\) (Vì Ot' là tia phân giác của \(\widehat {yOx'}\))
\(\widehat {tOt'} = 90^\circ \) (Vì Oy nằm giữa Ot và Ot')
-- Mod Toán 7 HỌC247
-


Chứng minh định lí Nếu mặt đường thẳng cắt hai đường thẳng phân biệt và trong các góc
bởi Nguyễn Trọng Nhân
 02/04/2019
02/04/2019
b/ Cho định lí: Nếu mặt đường thẳng cắt hai đường thẳng phân biệt và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì các góc đồng vị bằng nhau.
- Hãy cho biết giả thuyết của định lí do
- Hãy cho biết kết luận của định lí do
- Hãy chứng minh định lí đó.
Theo dõi (0) 1 Trả lời -


Chứng minh định lí :
Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau
Theo dõi (0) 1 Trả lời -


CMR nếu 2 đường thẳng song song thì 2 tia phân giác của cặp góc trong cùng phiá vuông goc với nhau
Theo dõi (0) 1 Trả lời -


cho địa lí hai đường thẳng cùng song song với đường thẳng thứ ba thì chúng song song với nhau. vẽ hình, ghi giả thiết, kết luận và chứng minh định lí đo
Theo dõi (0) 1 Trả lời -


Phát biểu định lý về hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba
bởi Aser Aser
 04/04/2019
04/04/2019
phát biểu định lý về hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba
phát biểu định lý về hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba
phát biểu định lí về một đường thẳng vuông góc với một trong hai đường thẳng song song
Theo dõi (0) 2 Trả lời -


Hãy phát biểu thành định lý được diễn tả bởi hình
bởi hai trieu
 06/04/2019
06/04/2019
a/Hãy phát biểu thành định lý được diễn tả bởi hình
b/Ghi GT, KL của định lý ở câu a dưới dạng ký hiệu
Theo dõi (0) 2 Trả lời -


Chứng minh định lý Nếu 2 đường thẳng xx' và yy' cắt nhau tại O và góc xOy=90 độ
bởi Nguyễn Lê Tín
 06/04/2019
06/04/2019
Chứng minh định lý :
Nếu 2 đường thẳng xx' và yy' cắt nhau tại O và \(\widehat{xOy}=90^0\) thì các góc yOx'; x'Oy' và y'Ox đều là góc vuông
Theo dõi (0) 2 Trả lời





