Giải bài tập Toán 11 Kết nối tri thức Bài 4: Phương trình lượng giác cơ bản

Một quả đạn pháo được bán ra khỏi nòng pháo với vận tốc ban đầu có độ lớn v₀ không đổi. Tìm góc bắn α để quả đạn pháo bay xa nhất, bỏ qua sức cản của không khí và coi quả đạn pháo được bắn ra từ mặt đất.

Cho hai phương trình 2x – 4 = 0 và (x – 2)(x\(^2\) + 1) = 0.

Tìm và so sánh tập nghiệm của hai phương trình trên.

Xét sự tương đương của hai phương trình sau: \(\frac{{x - 1}}{{x + 1}} = 0\) và x2−1=0

a) Quan sát Hình 1.19, tìm các nghiệm của phương trình đã cho trong nửa khoảng [0; 2π).

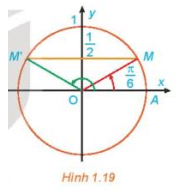
b) Dựa vào tính tuần hoàn của hàm số sin, hãy viết công thức nghiệm của phương trình đã cho.

Giải các phương trình sau:

a) sinx$=\frac{\sqrt{2}}{2}$;

b) sin 3x = – sin 5x.

a) Quan sát Hình 1.22a, tìm các nghiệm của phương trình đã cho trong nửa khoảng [– π; π).

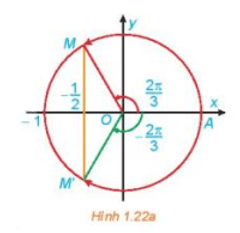
b) Dựa vào tính tuần hoàn của hàm số côsin, hãy viết công thức nghiệm của phương trình đã cho.

Giải các phương trình sau:

a) \(2\cos x =  - \sqrt 2 \);

b) cos 3x – sin 5x = 0.

Khi mặt trăng quay quanh Trái Đất, mặt đối diện với Trái Đất thường chỉ được Mặt Trời chiếu sáng một phần. Các pha của Mặt Trăng mô tả mức độ phần bề mặt của nó được Mặt Trời chiếu sáng. Khi góc giữa Mặt Trời, Trái Đất và Mặt Trăng là α$\left(0^0\le \alpha \le {360}^0\right)$thì tỉ lệ F của phần Mặt Trăng được chiếu sáng cho bới công thức:

F$=\frac{1}{2}\left(1-\cos \alpha \right)$.

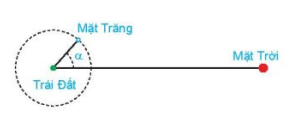
Xác định góc α tương ứng với các pha sau của Mặt Trăng.

a) F=0 (trăng mới)

b) F=0,25 (trăng lưỡi liềm)

c) F=0,5 (trăng bán nguyệt đầu tháng hoặc trăng bán nguyệt cuối tháng)

d) F=1 (trăng tròn)

a) Quan sát Hình 1.24, hãy cho biết đường thẳng y = 1 cắt đồ thị hàm số y = tan x tại mấy điểm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\)?

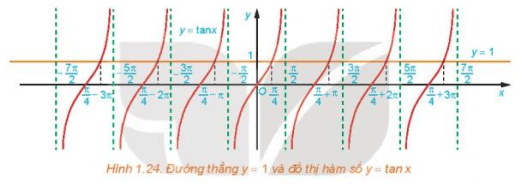
b) Dựa vào tính tuần hoàn của hàm tang, hãy viết công thức nghiệm của phương trình đã cho.

Giải các phương trình sau:

a) \(\sqrt 3 \tan 2x =  - 1\);                             

b) \(\tan 3x + \tan 5x = 0\)

a) Quan sát Hình 1.25, hãy cho biết đường thẳng y = – 1 cắt đồ thị hàm số y = cot x tại mấy điểm trên khoảng (0; π)?

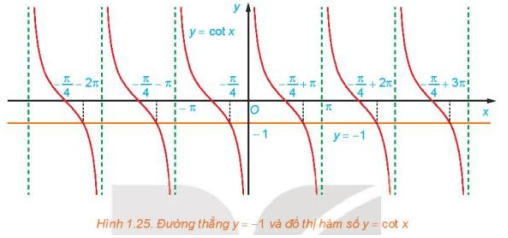
b) Dựa vào tính tuần hoàn của hàm côtang, hãy viết công thức nghiệm của phương trình đã cho.

Giải các phương trình sau:

a) cot x = 1;

b) \(\sqrt 3 \cot x + 1 = 0\)

Sử dụng máy tính cầm tay, tìm số đo độ và rađian của góc α, biết:

a) cos α = – 0,75;

b) tan α = 2,46;

c) cot α = – 6,18.

Giải các phương trình sau:

a) sinx = √3;

b) 2cosx = −√2;

c) √3tan(x/2+15°) = 1;

d) cot(2x−1) = cotπ/5.

Giải các phương trình sau:

a) sin 2x + cos 4x = 0;

b) cos 3x = – cos 7x.

Một quả đạn pháo được bắn ra khỏi nòng pháo với vận tốc ban đầu v₀ = 500 m/s hợp với phương ngang một góc α. Trong Vật lí, ta biết rằng, nếu bỏ qua sức cản của không khí và coi quả đạn pháo được bắn ra từ mặt đất thì quỹ đạo của quả đạn tuân theo phương trình \(y = \frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \), ở đó g = 9,8 m/s² là gia tốc trọng trường.

a) Tính theo góc bắn α tầm xa mà quả đạn đạt tới (tức là khoảng cách từ vị trí bắn đến điểm quả đạn chạm đất).

b) Tìm góc bắn α để quả đạn trúng mục tiêu cách vị trí đặt khẩu pháo 22 000 m.

c) Tìm góc bắn α để quả đạn đạt độ cao lớn nhất.

Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương trình

\[x = 2\cos \left( {5t - \frac{\pi }{6}} \right)\]

Ở đây, thời gian t tính bằng giây và quãng đường x tính bằng centimét. Hãy cho biết trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng bao nhiêu lần?

Giải các phương trình sau:

a) \(2\sin \left( {\frac{x}{3} + {{15}^0}} \right) + \sqrt 2 = 0\)

b) \(\cos \left( {2x + \frac{\pi }{5}} \right) = - 1\)

c) \(3\tan 2x + \sqrt 3 = 0\)

d) \(\cot \left( {2x - 3} \right) = \cot {15^0}\)

Giải các phương trình sau:

a) \(\sin \left( {2x + {{15}^0}} \right) + \cos \left( {2x - {{15}^0}} \right) = 0\)

b) \(\cos \left( {2x + \frac{\pi }{5}} \right) + \cos \left( {3x - \frac{\pi }{6}} \right) = 0\)

c) \(\tan x + \cot x = 0\)

d) \(\sin x + \tan x = 0\)

Giải các phương trình sau:

a) \(\left( {2 + \cos x} \right)\left( {3\cos 2x - 1} \right) = 0\)

b) \(2\sin 2x - \sin 4x = 0\)

c) \({\cos ^6}x - {\sin ^6}x = 0\)

d) \(\tan 2x\cot x = 1\)

Tìm các giá trị của x để giá trị tương ứng của các hàm số sau bằng nhau:

a) \(y = \cos \left( {2x - \frac{\pi }{3}} \right)\) và \(y = \cos \left( {x - \frac{\pi }{4}} \right)\)

b) \(y = \sin \left( {3x - \frac{\pi }{4}} \right)\) và \(y = \sin \left( {x - \frac{\pi }{6}} \right)\)

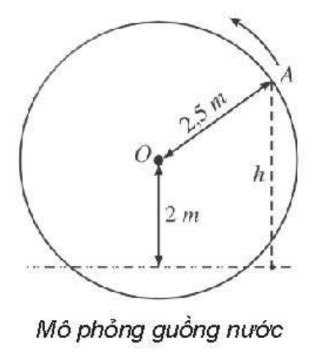
Một chiếc guồng nước có dạng hình tròn bán kính 2,5m; trục của nó đặt cách mặt nước 2m (hình bên). Khi guồng quay đều, khoảng cách h (mét) tính từ một chiếc gầu gắn tại điểm A trên guồng đến mặt nước là \(h = \left| y \right|\) trong đó \(y = 2 + 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right)\) với x là thời gian quay của guồng \(\left( {x \ge 0} \right),\) tính bằng phút; ta quy ước rằng \(y > 0\) khi gầu ở trên mặt nước và \(y < 0\) khi gầu ở dưới mặt nước.

a) Khi nào chiếc gầu ở vị trí cao nhất? Thấp nhất?

b) Chiếc gầu cách mặt nước 2 mét lần đầu tiên khi nào?

Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ t (ở đây t là số ngày tính từ ngày 1 tháng giêng) của một năm không nhuận được mô hình hóa bởi hàm số:

\(L\left( t \right) = 12 + 2,83\sin \left( {\frac{{2\pi }}{{365}}\left( {t - 80} \right)} \right)\) với \(t \in \mathbb{Z}\) và \(0 < t \le 365\)

a) Vào ngày nào trong năm thì thành phố A có ít giờ ánh sáng mặt trời nhất?

b) Vào ngày nào trong năm thì thành phố A có nhiều giờ ánh sáng mặt trời nhất?

c) Vào ngày nào trong năm thì thành phố A có khoảng 10 giờ ánh sáng mặt trời?