Bài tập 1.29 trang 24 SBT Toán 11 Tập 1 Kết nối tri thức
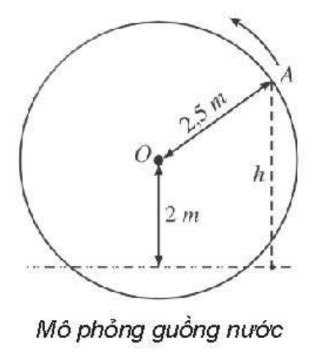
Một chiếc guồng nước có dạng hình tròn bán kính 2,5m; trục của nó đặt cách mặt nước 2m (hình bên). Khi guồng quay đều, khoảng cách h (mét) tính từ một chiếc gầu gắn tại điểm A trên guồng đến mặt nước là h=|y| trong đó y=2+2,5sin2π(x−14) với x là thời gian quay của guồng (x≥0), tính bằng phút; ta quy ước rằng y>0 khi gầu ở trên mặt nước và y<0 khi gầu ở dưới mặt nước.
a) Khi nào chiếc gầu ở vị trí cao nhất? Thấp nhất?
b) Chiếc gầu cách mặt nước 2 mét lần đầu tiên khi nào?
Hướng dẫn giải chi tiết Bài 1.29
a) Vì −1≤sin2π(x−14)≤1 nên −2,5≤2,5sin2π(x−14)≤2,5.
Do đó, −0,5=2−2,5≤2+2,5sin2π(x−14)≤2+2,5=4,5∀x∈R.
Suy ra, gầu ở vị trí cao nhất khi:
sin2π(x−14)=1⇔2π(x−14)=π2+k2π⇔x=12+k(k∈Z).
Vì gầu ở vị trí cao nhất tại các thời điểm 12,32,52,... phút.
Tương tự, gầu ở vị trí thấp nhất khi:
sin2π(x−14)=−1⇔2π(x−14)=−π2+k2π⇔x=k(k∈Z).
Vì gầu ở vị trí cao nhất tại các thời điểm 0, 1, 2, 3… phút.
b) Gầu cách mặt nước 2m khi:
2+2,5sin2π(x−14)=2⇔2,5sin2π(x−14)=0⇔2π(x−14)=kπ⇔x=14+k2(k∈Z).
Vậy chiếc gầu cách mặt nước 2m lần đầu tại thời điểm x=14 phút.
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





