Toán 11 Cánh Diều Chương 8 Bài 2: Đường thẳng vuông góc với mặt phẳng

Đường thẳng d được gọi là vuông góc với mặt phẳng (P) nếu đường thẳng d vuông góc với mọi đường thẳng a trong mặt phẳng (P), kí hiệu \(d\bot \left( P \right)\) hoặc \(\left( P \right)\bot d\).

 

 

Định lí

Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.

 

Tính chất 1

Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

 

Tính chất 2

Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.

 

Tính chất 3

- Cho hai đường thẳng song song. Một mặt phẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.  - Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

 

Tính chất 4

- Cho hai mặt phẳng song song. Một đường thẳng vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.  - Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

 

Gọi M' là giao điểm của đường thẳng d và mặt phẳng (P). Điểm M’ được gọi là hình chiếu vuông góc (hay hình chiếu) của điểm M trên mặt phẳng (P).

 

 

Định nghĩa

Cho mặt phẳng (P). Quy tắc đặt tương ứng mỗi điểm M trong không gian với hình chiếu vuông góc M' của điểm đó lên mặt phẳng (P) được gọi là phép chiếu vuông góc lên mặt phẳng (P).

 

Nhận xét:

Vì phép chiếu vuông góc là một trường hợp đặc biệt của phép chiếu song song nên phép chiếu vuông góc có đầy đủ các tính chất của phép chiếu song song.

 

Định lí

Cho đường thẳng a không vuông góc với mặt phẳng (P) và đường thẳng d nằm trong mặt phẳng (P). Khi đó, d vuông góc với a khi và chỉ khi d vuông góc với hình chiếu a’ của a trên (P).

 

 

Chứng minh

- Nếu a nằm trong (P) thì kết quả là hiển nhiên.

- Ta xét trường hợp a không nằm trong (P). Lấy điểm \(M\in a\). Gọi H là hình chiếu của M trên (P) thì a’ đi qua H. Gọi (Q) là mặt phẳng chứa hai đường thẳng a và MH. Do \(MH\bot (P)\) mà \(d\subset (P)\) nên \(MH\bot d\).

Giả sử \(d\bot a'\). Khi đó, d vuông góc với hai đường thẳng cắt nhau trong mặt phẳng (Q) là a' và MH. Suy ra \(d\bot (Q)\), mà \(a\subset (Q)\) nên \(d\bot a\).

Giả sử \(d\bot a\). Khi đó, bằng cách chứng minh tương tự như trên, ta có: \(d\bot a'\).

Bài 1. Cho hình chóp S.ABCD đáy ABCD là hình thang vuông tại A và B, \(SA \bot (ABCD)\), AD = 2a, AB = BC = a. Chứng minh rằng: Tam giác SCD vuông?

 

Hướng dẫn giải

 

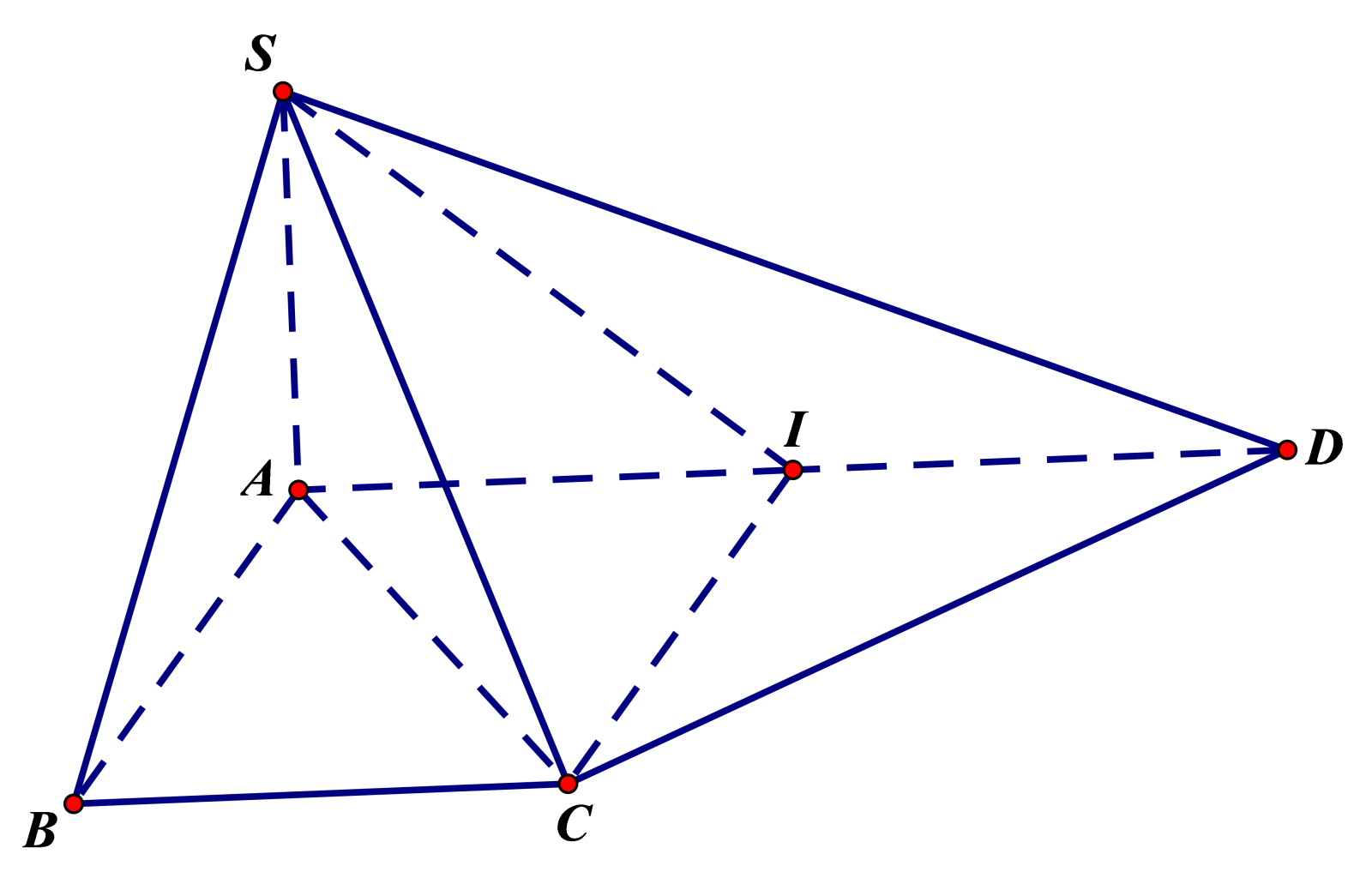
Ta có: \(\left. \begin{array}{l} SA \bot (ABCD)\\ CD \subset (ABCD) \end{array} \right\} \Rightarrow SA \bot CD(1)\)

Gọi I là trung điểm của AD. Tứ giác ABCI là hình vuông.

Do đó, \(\widehat {ACI} = {45^0}.\) (*)

Mặt khác tam giác CID vuông cân tại I nên \(\widehat {BCI} = {45^0}.\) (**)

Từ (*) (**) suy ra: \(\widehat {ACD} = {90^0}\) hay \(AC \bot CD (2)\).

Từ (1) và (2) suy ra: \(CD \bot (SAC) \Rightarrow CD \bot SC\).

Hay tam giác SCD vuông tại C.

a) Chứng minh rằng: \(BC \bot (SAC)\).

b) Gọi E là hình chiếu vuông góc của A trên SC. Chứng minh rằng: \(AE \bot (SBC).\)

c) Gọi (P) là mặt phẳng qua AE và vuông góc với SB, (P) giao với SB tại D. Đường thẳng DE cắt BC tại F. Chứng minh rằng: \(AF \bot (SAB).\)

 

Hướng dẫn giải

 

a) Ta có: \(BC \bot AC{\rm{ }}(gt){\rm{ (1)}}\)

Mặt khác: \(\left. \begin{array}{l} SA \bot (ABC)\\ BC \subset (ABC) \end{array} \right\} \Rightarrow SA \bot BC\,\,(2)\)

Từ (1) và (2) suy ra: \(BC \bot (SAB).\)

b) Ta có: \(AE \bot SC{\rm{ (3) (gt)}}\)

Theo câu a ta có: \(BC \bot (SAB) \Rightarrow AE \bot BC{\rm{ (4)}}\)

Từ (3) (4) suy ra: \(AE \bot (SBC).\)

c) Ta có mặt phẳng (P) chính là mặt phẳng (ADE).

Từ \(\left. \begin{array}{l} SA \bot (ABC)\\ AF \subset (ABC) \end{array} \right\} \Rightarrow AF \bot SA{\rm{ (5)}}\)

Do \(SB \bot (ADE) \Rightarrow AF \bot SB{\rm{ (6)}}\).

Từ (5) (6) suy ra: \(AF \bot (SAB).\)

Học xong bài học này, em sẽ:

– Giải thích được mối liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng.

– Nhận biết được khái niệm phép chiếu vuông góc.

Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 11 Cánh Diều Chương 8 Bài 2 cực hay có đáp án và lời giải chi tiết. 

• Câu 1:

  Cho a, b, c là các đường thẳng trong không gian. Tìm mệnh đề sai trong các mệnh đề cho bên dưới?

  • A. Nếu a ⊥ b và b ⊥ c thì a // c.
  • B. Nếu a vuông góc với mặt phẳng (α) và b // (α) thì a ⊥ b.
  • C. Nếu a // b và b ⊥ c thì c ⊥ a.
  • D. Nếu a ⊥ b, b ⊥ c và a cắt c thì b vuông góc với mặt phẳng (a, c).

• Câu 2:

  Cho hình chóp S.ABC có cạnh SA ⊥ (ABC) và đáy ABC là tam giác cân ở C. Gọi H và K lần lượt là trung điểm của AB và SB. Khẳng định nào dưới đây sai?

  

  • A. CH ⊥ SA
  • B. CH ⊥ SB
  • C. CH ⊥ AK
  • D. AK ⊥ SB

• Câu 3:

  Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh bên SA ⊥ (ABC). Mp (P) đi qua trung điểm M của AB và vuông góc với SB cắt AC, SC, SB lần lượt tại N, P, Q. Tứ giác MNPQ là hình gì?

  • A. Hình thang vuông.
  • B. Hình thang cân.
  • C. Hình bình hành.
  • D. Hình chữ nhật.

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!

Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 11 Cánh Diều Chương 8 Bài 2 để giúp các em nắm vững bài học và các phương pháp giải bài tập.

Khởi động trang 80 SGK Toán 11 Tập 2 Cánh diều - CD

Hoạt động 1 trang 80 SGK Toán 11 Tập 2 Cánh diều - CD

Hoạt động 2 trang 81 SGK Toán 11 Tập 2 Cánh diều - CD

Luyện tập 1 trang 81 SGK Toán 11 Tập 2 Cánh diều - CD

Hoạt động 3 trang 81 SGK Toán 11 Tập 2 Cánh diều - CD

Luyện tập 2 trang 82 SGK Toán 11 Tập 2 Cánh diều - CD

Hoạt động 4 trang 82 SGK Toán 11 Tập 2 Cánh diều - CD

Luyện tập 3 trang 83 SGK Toán 11 Tập 2 Cánh diều - CD

Hoạt động 5 trang 83 SGK Toán 11 Tập 2 Cánh diều - CD

Luyện tập 4 trang 84 SGK Toán 11 Tập 2 Cánh diều - CD

Hoạt động 6 trang 84 SGK Toán 11 Tập 2 Cánh diều - CD

Luyện tập 5 trang 85 SGK Toán 11 Tập 2 Cánh diều - CD

Hoạt động 7 trang 85 SGK Toán 11 Tập 2 Cánh diều - CD

Luyện tập 6 trang 86 SGK Toán 11 Tập 2 Cánh diều - CD

Hoạt động 8 trang 87 SGK Toán 11 Tập 2 Cánh diều - CD

Luyện tập 7 trang 87 SGK Toán 11 Tập 2 Cánh diều - CD

Bài 1 trang 88 SGK Toán 11 Tập 2 Cánh diều - CD

Bài 2 trang 88 SGK Toán 11 Tập 2 Cánh diều - CD

Bài 3 trang 88 SGK Toán 11 Tập 2 Cánh diều - CD

Bài 4 trang 88 SGK Toán 11 Tập 2 Cánh diều - CD

Bài 5 trang 88 SGK Toán 11 Tập 2 Cánh diều - CD

Bài tập 6 trang 93 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 7 trang 94 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 8 trang 94 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 9 trang 94 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 10 trang 94 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 11 trang 94 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 12 trang 94 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 13 trang 94 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 14 trang 95 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 15 trang 95 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 16 trang 95 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 17 trang 95 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 18 trang 95 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 19 trang 95 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 20 trang 95 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 21 trang 95 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 22 trang 95 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 23 trang 95 SBT Toán 11 Tập 2 Cánh diều - CD

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán học HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!