Bài tập 19 trang 95 SBT Toán 11 Tập 2 Cánh diều
Cho hình tứ diện ABCD có AB ⊥ (BCD), các tam giác BCD và ACD là những tam giác nhọn. Gọi H, K lần lượt là trực tâm của các tam giác BCD, ACD. Chứng minh rằng:
a) AD ⊥ CH;
b*) HK ⊥ (ACD).
Hướng dẫn giải chi tiết Bài tập 19
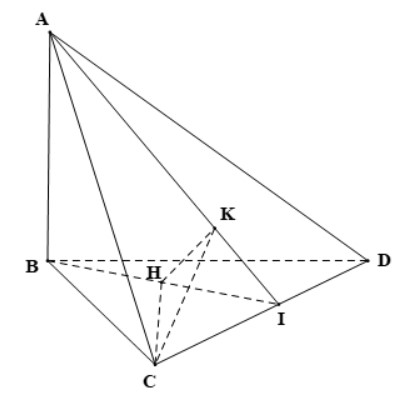
a) Vì AB ⊥ (BCD), CH ⊂ (BCD) nên AB ⊥ CH hay CH ⊥ AB.
Do H là trực tâm của tam giác BCD nên CH ⊥ BD.
Ta có: CH ⊥ AB, CH ⊥ BD và AB ∩ BD = B trong (ABD).
Suy ra CH ⊥ (ABD).
Mà AD ⊂ (ABD) nên CH ⊥ AD hay AD ⊥ CH.
b) Trong (BCD), gọi I = BH ∩ CD mà H là trực tâm của tam giác BCD nên BI ⊥ CD.
Lại có: AB ⊥ (BCD), CD ⊂ (BCD) nên AB ⊥ CD.
- Ta có: CD ⊥ BI, CD ⊥ AB và BI ∩ AB = B trong (ABI).
Suy ra CD ⊥ (ABI).
Mà HK ⊂ (ABI) nên CD ⊥ HK. (1)
- Vì K là trực tâm của tam giác ACD nên CK ⊥ AD.
Ta có: AD ⊥ CH (theo câu a), AD ⊥ CK và CH ∩ CK = C trong (CHK).
Suy ra: AD ⊥ (CHK).
Mà HK ⊂ (CHK) nên AD ⊥ HK. (2)
Từ (1), (2) kết hợp với CD ∩ AD = D trong (ACD) nên ta có HK ⊥ (ACD).
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





