Toán 11 Cánh Diều Chương 8 Bài 5: Khoảng cách

Định nghĩa 

- Trong Hình bên dưới, ta có \(d(M, \Delta ) = MH\).

Chú ý: Khi điểm M thuộc đường thẳng \( \Delta \) thì \(d(M, \Delta ) = 0\).

Định nghĩa

Chú ý: Khi điểm M thuộc mặt phẳng (P) thì \( d(M, (P))=0 \).

Định nghĩa

- Trong Hình bên dưới, ta có \(d( \Delta, {\Delta}') =AB\) với \(A \in \Delta, B \in {\Delta}'\), \(AB \bot \Delta, AB \bot {\Delta}' \) và \( \Delta // {\Delta}'\).

Định nghĩa 

- Trong hình dưới, ta có: \(d( \Delta , (P))=MM'=h\), trong đó \(M \in \Delta, M' \in (P)\), \(MM' \bot (P)\) và\(\Delta // (P)\).

Định nghĩa

- Trong hình dưới, ta có: \(d((P),(Q)) = IK = h\) với \(I \in (P), K \in (Q), IK \bot (P), IK \bot (Q)\) và \((P) // (Q)\).

Định nghĩa 

Nhận xét:

- Gọi mặt phẳng chứa b và song song với a là (P), hình chiếu của a trên (P) là a’, giao điểm của a’ và b là K. Khi đó, HK là đoạn vuông góc chung của hai đường thẳng chéo nhau a, b (Hình a). Ngoài ra, ta cũng có \(d(a, b) = d(a, (P))\).

- Khi \(a \bot b\), ta có thể làm như sau: Gọi mặt phẳng đi qua b và vuông góc với a là (P), giao điểm của a và (P) là H, hình chiếu của H trên b là K. Khi đó HK là đoạn vuông góc chung của hai đường thẳng chéo nhau a, b (Hình b).

Bài 1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = SB = SC = SD = \(a\sqrt2\). Tính khoảng cách giữa hai đường thẳng chéo nhau AD và SC?

Hướng dẫn giải

Vì AD // BC nên d(AD, SC) = d(AD, (SBC)) = d(A, (SBC)).

Ta có \(AO\cap (SBC)=C\) và \(\frac{CO}{CA}=\frac{1}{2}\), do đó:

d(A,(SBC)) = 2.d(O,(SBC)).

\(SO \bot (ABCD)\) nên \(SO \bot BC\)

Kẻ \(SI \bot BC\) thì I là trung điểm của BC.

Suy ra: \(BC \bot (SOI)\Rightarrow (SBC)\bot (SOI)\)

\((SBC)\cap (SOI)=SI\)

Kẻ \(OI \bot SI (H\in SI).\) Khi đó \(d(O,(SBC)) = OH\)

Xét tam giác SOI vuông tại O, theo hệ thức lượng trong tam giác vuông ta có:

\(\frac{1}{{O{H^2}}} = \frac{1}{{O{J^2}}} + \frac{1}{{O{S^2}}}\) mà \(OJ = \frac{1}{2}.a;\,\,SO = \sqrt {S{C^2} - C{O^2}} = \frac{{a\sqrt 6 }}{2}\)

Suy ra: \(OH = \frac{{\sqrt {42} }}{{14}}a.\)

Vậy: \(d(AD,SC) = 2.\frac{{\sqrt {42} }}{{14}}a = \frac{{\sqrt {42} }}{7}.a.\)

Bài 2. Cho tứ diện SABC có tam giác ABC vuông cân đỉnh B, AB = a, SA vuông góc với mặt phẳng (ABC) và SA = a.

a) Chứng minh (SAB) \(\bot\) (SBC) ?

b) Tính khoảng cách từ điểm A đến mp(SBC)?

c) Gọi I là trung điểm của AB. Tính khoảng cách từ điểm I đến mp(SBC)?

Hướng dẫn giải

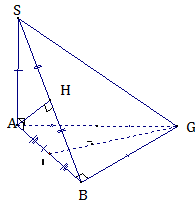
a) Theo giả thiết ta có: \(SA \bot (ABC)\).

Suy ra \(SA \bot BC\) (1).

Mà \(AB \bot BC\) (giả thiết) (2).

Từ (1) và (2) ta suy ra: \(BC \bot (SAB)\Rightarrow (SBC) \bot (SAB).\)

b) Ta có: \((SAB)\cap (SBC)=SB\).

Kẻ \(AH \bot SB (H\in SB).\)

Do tam giác SAB vuông cân nên H là trung điểm của SB.

Khi đó: \(AH \bot (SBC)\) nên \(d(A, (SBC))=AH\).

Xét tam giác SAB vuông cân tại A. Theo hệ thức lượng trong tam giác vuông ta có:

\(\frac{1}{{A{H^2}}} = \frac{1}{{A{S^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{a^2}}} \Rightarrow AH = \frac{{a\sqrt 2 }}{2}.\)

c) Ta có: \(AB\cap (SBC)=B\) và \(\frac{BI}{BA}=\frac{1}{2}\) (do I là trùng điểm của AB) nên:

\(d(I,(SBC)) = \frac{1}{2}d(A,(SBC)) = \frac{1}{2}.\frac{{a\sqrt 2 }}{2} = \frac{{a\sqrt 2 }}{4}.\)

a) Tính khoảng cách từ A đến mặt phẳng \(\left (\alpha \right )\)?

b) Tính khoảng cách từ E đến mặt phẳng \(\left (\alpha \right )\), từ đó suy ra khoảng cách từ I – trung điểm của AM đến mặt phẳng \(\left (\alpha \right )\)?

c) Gọi d là đường thẳng qua I song song với mặt phẳng \(\left (\alpha \right )\). Lấy J thuộc d, tính khoảng cách từ J đến mặt phẳng \(\left (\alpha \right )\)?

d) Gọi C là chân đường vuông góc của J lên mặt phẳng \(\left (\alpha \right )\). D là trung điểm của JC. Tính khoảng cách từ D đến mặt phẳng \(\left (\alpha \right )\)?

Hướng dẫn giải

a) H là hình chiếu vuông góc của A lên mặt phẳng \(\left (\alpha \right )\) nên: d(A,\(\left (\alpha \right )\)) = AH = h.

b) Gọi P là chân đường vuông góc của E lên mặt phẳng \(\left (\alpha \right )\).

Khi đó:  d(E, \(\left (\alpha \right )\)) = EP.

Ta có : EP // AH (đều vuông góc với mp \(\left (\alpha \right )\)) và M, P, H thẳng hàng.

Theo định lí Tallet ta có: 

\(\frac{{EP}}{{AH}} = \frac{{ME}}{{MA}}=k\)

Khi đó: EP = k.AH hay d(E, (a)) = k.h (1).

Vì I là trung điểm của AM nên:

\(d(I,\left( \alpha \right)) = \frac{1}{2}.h\) (áp dụng kết quả (1) với \(k=\frac{1}{2}\)).

c) Ta có: IJCQ là hình chữ nhật nên IQ=JC

Do đó: \(d(J,\left( \alpha \right)) = d(I,\left( \alpha \right)) = \frac{1}{2}.h.\)

d) D là trung điểm của JC nên \(\frac{CD}{CJ}=\frac{1}{2}.\)

Suy ra: \(d(Q,\left( \alpha \right)) = \frac{1}{2}d(J,\left( \alpha \right)) = \frac{1}{2}.\frac{1}{2}.h = \frac{1}{4}.h\).

Học xong bài học này, em sẽ hoàn thành mục tiêu sau: Tính được các loại khoảng cách trong không gian.

Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 11 Cánh Diều Chương 8 Bài 5 cực hay có đáp án và lời giải chi tiết. 

• Câu 1:

  Trong các mệnh đề sau, hãy chọn mệnh đề đúng?

  • A. Đường vuông góc chung của hai đường thẳng chéo nhau thì vuông góc với mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
  • B. Một đường thẳng là đường vuông góc chung của hai đường thẳng chéo nhau nếu nó vuông góc với cả hai đường thẳng đó.
  • C. Đường vuông góc chung của hai đường thẳng chéo nhau thì nằm trong mặt phẳng chứa đường thẳng này và vuông góc với đường thẳng kia.
  • D. Một đường thẳng là đường vuông góc chung của hai đường thẳng chéo nhau nếu nó cắt cả hai đường thẳng đó.

• Câu 2:

  Cho hình lăng trụ tam giác \(ABC.{A}'{B}'{C}'\) có các cạnh bên hợp với đáy những góc bằng \(60{}^\circ \), đáy \(ABC\) là tam giác đều và \({A}'\) cách đều \(A\), \(B\), \(C\). Tính k/c giữa 2 đáy của hình lăng trụ?

  • A. \(a\).             
  • B. \(a\sqrt{2}\).       
  • C. \(\frac{a\sqrt{3}}{2}\).  
  • D. \(\frac{2a}{3}\).

• Câu 3:

  Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\) có cạnh bằng \(1\) (đvdt). K/c giữa \(AA'\) và \(BD'\) bằng?

  • A. \(\frac{\sqrt{3}}{3}\).
  • B. \(\frac{\sqrt{2}}{2}\).         
  • C. \(\frac{2\sqrt{2}}{5}\).  
  • D. \(\frac{3\sqrt{5}}{7}\).

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!

Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 11 Cánh Diều Chương 8 Bài 5 để giúp các em nắm vững bài học và các phương pháp giải bài tập.

Hoạt động 1 trang 101 SGK Toán 11 Tập 2 Cánh diều - CD

Luyện tập 1 trang 101 SGK Toán 11 Tập 2 Cánh diều - CD

Hoạt động 2 trang 102 SGK Toán 11 Tập 2 Cánh diều - CD

Luyện tập 2 trang 102 SGK Toán 11 Tập 2 Cánh diều - CD

Hoạt động 3 trang 102 SGK Toán 11 Tập 2 Cánh diều - CD

Luyện tập 3 trang 103 SGK Toán 11 Tập 2 Cánh diều - CD

Hoạt động 4 trang 103 SGK Toán 11 Tập 2 Cánh diều - CD

Luyện tập 4 trang 104 SGK Toán 11 Tập 2 Cánh diều - CD

Hoạt động 5 trang 105 SGK Toán 11 Tập 2 Cánh diều - CD

Luyện tập 5 trang 106 SGK Toán 11 Tập 2 Cánh diều - CD

Bài 1 trang 106 SGK Toán 11 Tập 2 Cánh diều - CD

Bài 2 trang 106 SGK Toán 11 Tập 2 Cánh diều - CD

Bài 3 trang 106 SGK Toán 11 Tập 2 Cánh diều - CD

Bài 4 trang 106 SGK Toán 11 Tập 2 Cánh diều - CD

Bài 5 trang 106 SGK Toán 11 Tập 2 Cánh diều - CD

Bài tập 45 trang 109 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 46 trang 110 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 47 trang 110 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 48 trang 110 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 49 trang 110 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 50 trang 110 SBT Toán 11 Tập 2 Cánh diều - CD

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán học HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!