Toán 11 Cánh Diều Chương 8 Bài 1: Hai đường thẳng vuông góc

Định nghĩa

Nhận xét

- Góc giữa hai đường thẳng a, b không phụ thuộc vào vị trí điểm 0. Thông thường, khi tìm góc giữa hai đường thẳng a, b, ta chọn O thuộc a hoặc O thuộc b.

- Góc giữa hai đường thẳng a, b bằng góc giữa hai đường thẳng b, a, tức là \((a, b) = (b, a)\).

- Góc giữa hai đường thẳng không vượt quá \({{90}^{0}}\).

- Nếu \(a/ / b\) thì \((a, c) = (b, c)\) với mọi đường thẳng c trong không gian.

Định nghĩa

- Khi hai đường thẳng a và b vuông góc với nhau, ta kí hiệu \(a \bot b\).

Nhận xét:

Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường còn lại.

Bài 1. Cho tứ diện ABCD có AB ⊥ AC và AB ⊥ BD. Gọi P và Q lần lượt là trung điểm của AB và CD. CMR: AB và PQ là hai đường thẳng vuông góc với nhau?

Hướng dẫn giải

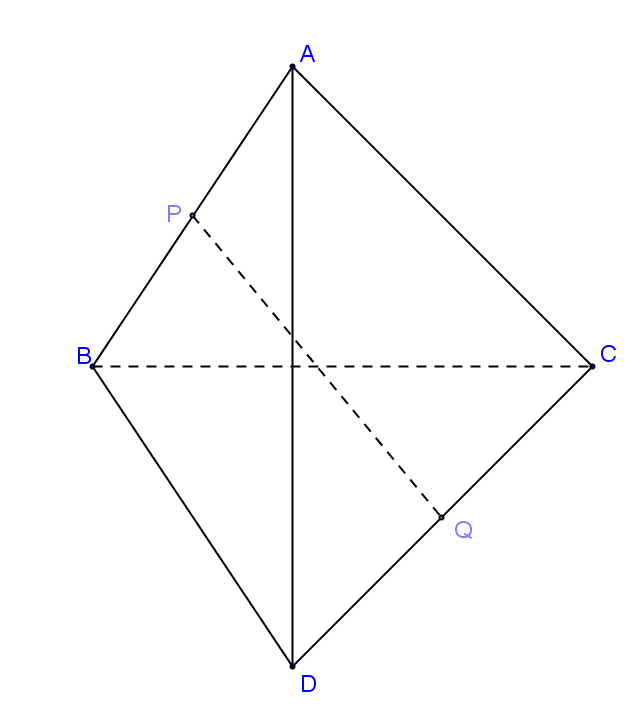
Ta có: \(\overrightarrow {PQ} = \overrightarrow {PA} + \overrightarrow {AC} + \overrightarrow {CQ}\)  

Và: \(\overrightarrow {PQ} = \overrightarrow {PB} + \overrightarrow {BD} + \overrightarrow {DQ}\)  

Do đó: \(2\overrightarrow {PQ} = \overrightarrow {AC} + \overrightarrow {BD}\)  

Vậy: \(2.\overrightarrow {PQ} .\overrightarrow {AB} = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right).\overrightarrow {AB} = \overrightarrow {AC} .\overrightarrow {AB} + \overrightarrow {BD} .\overrightarrow {AB} = 0\)

Hay \(\overrightarrow {PQ} .\overrightarrow {AB} = 0\) Tức là: \(PQ \bot AB.\)

Bài 2. Cho hình chóp tam giác S.ABC có SA = SB =SC và có \(\widehat {{\rm{ASB}}} = \widehat {BSC} = \widehat {CSA}.\) CMR: \(SA \bot BC, SB\bot AC, SC \bot AB.\)?

Hướng dẫn giải

Xét các tích vô hướng: \(\overrightarrow {SA} .\overrightarrow {BC} ,\overrightarrow {SB} .\overrightarrow {AC} ,\overrightarrow {SC} .\overrightarrow {AB} .\)

Ta có: 

\(\begin{array}{l} \overrightarrow {SA} .\overrightarrow {BC} = \overrightarrow {SA} .(\overrightarrow {SC} - \overrightarrow {SB} ) = \overrightarrow {SA} .\overrightarrow {SC} - \overrightarrow {SA} .\overrightarrow {SB} \\ = \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {SC} } \right|.c{\rm{os}}\widehat {{\rm{CSA}}} - \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {SB} } \right|c{\rm{os}}\widehat {{\rm{ASB}}} \end{array}\)

Theo giả thuyết: \(\left| {\overrightarrow {SB} } \right| = \left| {\overrightarrow {SC} } \right|\)

Và: \(c{\rm{os}}\widehat {{\rm{CSA}}} = c{\rm{os}}\widehat {{\rm{ASB}}} \Rightarrow \overrightarrow {SA} .\overrightarrow {BC} = 0\)

Vậy: \(SA \bot BC.\)

Chứng minh tương tự ta có: \(SB\bot AC, SC \bot AB.\)

a) \(\overrightarrow {AB} ,\overrightarrow {EG} .\)

c) \(\overrightarrow {AB} ,\overrightarrow {DH}\).

Hướng dẫn giải

a) Vì EG // AC nên góc giữa \(\overrightarrow {AB} ,\overrightarrow {EG}\) cũng bằng góc giữa \(\overrightarrow {AB}\) và \(\overrightarrow {AC}\)

Vậy \(\left( {\overrightarrow {AB} ;\overrightarrow {EG} } \right) = \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = {45^0}.\)

b)  Vì AB // DG nên góc giữa \(\overrightarrow {AB} ,\overrightarrow {DH}\) cũng bằng góc giữa \(\overrightarrow {DC}\) và \(\overrightarrow {DH}\)

Vậy \(\left( {\overrightarrow {AB} ;\overrightarrow {DH} } \right) = \left( {\overrightarrow {AB} ;\overrightarrow {DH} } \right) = {45^0}.\)

Bài 4. Cho tứ diện ABCD có AB = AC = AD = a, \(\widehat {BAC} = \widehat {BAD} = {60^0}.\).

a) Chứng minh rằng AB vuông góc CD.

b) Nếu I, J lần lượt là trung điểm của AB và CD thì \(AB \bot IJ.\)  

Hướng dẫn giải

a) Ta có:

\(\begin{array}{l} \overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} \left( {\overrightarrow {AD} - \overrightarrow {AC} } \right) = \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC} \\ = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos BAD - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos BAC \end{array}\)

Mặt khác ta có: \(AB = AC = AD,\widehat {BAC} = \widehat {BAD}\)

Nên: \(\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos BAD - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos BAC = 0\)

Vậy AB vuông góc với CD.

b) ) Do I, J là trung điểm của AB và CD nên ta có: \(\overrightarrow {IJ} = \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right)\)

Do đó: 

\(\begin{array}{l} \overrightarrow {AB} .\overrightarrow {IJ} = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AB} \overrightarrow {BC} } \right) = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AB} \overrightarrow {BA} + \overrightarrow {AB} .\overrightarrow {AC} } \right)\\ = \frac{1}{2}\left( {\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|\cos {{60}^0} - {{\overrightarrow {AB} }^2} + \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|\cos {{60}^0}} \right)\\ = \frac{1}{2}\left( {\frac{1}{2}{a^2} - {a^2} + \frac{1}{2}{a^2}} \right) = 0 \end{array}\)

Vậy AB và IJ vuông góc nhau.

Học xong bài học này, em sẽ:

- Nhận biết góc giữa hai đường thẳng, và hai đường thẳng vuông góc.

- Chứng minh hai đường thẳng vuông góc trong một số tình huống đơn giản.

- Vận dụng kiến thức về quan hệ vuông góc giữa hai đường thẳng để mô tả một số hình ảnh thực tế.

Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 11 Cánh Diều Chương 8 Bài 1 cực hay có đáp án và lời giải chi tiết. 

• Câu 1:

  Trong không gian mệnh đề nào đúng trong các mệnh đề bên dưới?

  • A. Góc giữa đường thẳng \(a\) và \(b\)bằng góc giữa đường thẳng \(a\)và \(c\) thì \(b\) Song song với \(c\). 
  • B. Góc giữa hai đường thẳng bằng hoặc bù với góc giữa hai véc tơ chỉ phương của hai đường thẳng đó.
  • C. Góc giữa hai đường thẳng là góc nhọn. 
  • D. Góc giữa đường thẳng \(a\)và \(b\) bằng góc giữa hai đường thẳng \(a\) và \(c\) khi \(b\) Song song hoặc trùng với \(c\).

• Câu 2:

  Cho hình lập phương \(ABCD{A}'{B}'{C}'{D}'\). Khẳng định nào bên dưới là sai? 

  • A. Góc giữa hai đường thẳng \({B}'{D}'\) và \(A{A}'\) bằng \(60{}^\circ \). 
  • B. Góc giữa hai đường thẳng \(AC\) và \({B}'{D}'\) bằng \(90{}^\circ \). 
  • C. Góc giữa hai đường thẳng \(AB\) và \({D}'C\) bằng \(45{}^\circ \). 
  • D. Góc giữa hai đường thẳng \({D}'C\) và \({A}'{C}'\) bằng \(60{}^\circ \).

• Câu 3:

  Cho hình chóp \(S.ABCD\) có tất cả các cạnh đều bằng\(~a\). Gọi \(I\) và \(J\) lần lượt là trung điểm của \(SC\) và \(BC\). Tính số đo của góc \(\left( \text{ }IJ,\text{ }CD \right)\)?

  • A. \(90{}^\circ \).      
  • B. \(45{}^\circ \).  
  • C. \(30{}^\circ \).  
  • D. \(60{}^\circ \).

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!

Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 11 Cánh Diều Chương 8 Bài 1 để giúp các em nắm vững bài học và các phương pháp giải bài tập.

Khởi động trang 77 SGK Toán 11 Tập 2 Cánh diều - CD

Hoạt động 1 trang 77 SGK Toán 11 Tập 2 Cánh diều - CD

Luyện tập 1 trang 78 SGK Toán 11 Tập 2 Cánh diều - CD

Hoạt động 2 trang 78 SGK Toán 11 Tập 2 Cánh diều - CD

Luyện tập 2 trang 79 SGK Toán 11 Tập 2 Cánh diều - CD

Bài 1 trang 79 SGK Toán 11 Tập 2 Cánh diều - CD

Bài 2 trang 79 SGK Toán 11 Tập 2 Cánh diều - CD

Bài 3 trang 79 SGK Toán 11 Tập 2 Cánh diều - CD

Bài 4 trang 79 SGK Toán 11 Tập 2 Cánh diều - CD

Bài tập 1 trang 88 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 2 trang 89 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 3 trang 89 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 4 trang 89 SBT Toán 11 Tập 2 Cánh diều - CD

Bài tập 5 trang 89 SBT Toán 11 Tập 2 Cánh diều - CD

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán học HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!