Bài tập 17 trang 95 SBT Toán 11 Tập 2 Cánh diều - CD

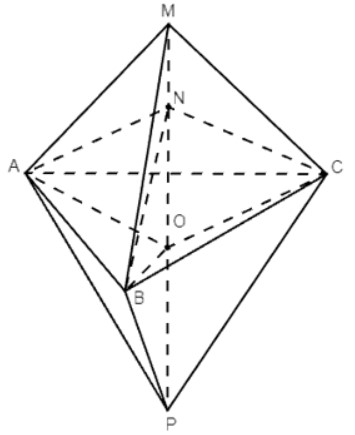
Gọi O là tâm đường tròn ngoại tiếp của tam giác ABC.

Khi đó OA = OB = OC.

- Trường hợp 1: Ba điểm M, N, P đều không thuộc mặt phẳng (ABC).

Xét hình chóp M.ABC có MA = MB = MC nên theo kết quả của Bài 16, trang 95, Sách bài tập Toán 11, Tập hai ta có: MO ⊥ (ABC)

Tương tự, từ NA = NB = NC, PA = PB = PC ta cũng có NO ⊥ (ABC), PO ⊥ (ABC).

Ta thấy: MO, NO, PO cùng đi qua điểm O và vuông góc với mặt phẳng (ABC).

Do đó ba đường thẳng MO, NO, PO trùng nhau hay M, N, P thẳng hàng.

- Trường hợp 2: Trong ba điểm M, N, P có một điểm nằm trên (ABC).

Mà MA = MB = MC, NA = NB = NC, PA = PB = PC nên không mất tính tổng quát ta giả sử điểm M nằm trên (ABC).

Ta có MA = MB = MC, OA = OB = OC và M, O cùng nằm trong mp (ABC)

Suy ra: M ≡ O.

Tương tự trường hợp 1, từ NA = NB = NC, PA = PB = PC nên cũng ta có:

NO ⊥ (ABC), PO ⊥ (ABC).

Ta thấy: NO, PO cùng đi qua điểm O và vuông góc với mặt phẳng (ABC).

Do đó hai đường thẳng NO, PO trùng nhau hay O, N, P thẳng hàng hay M, N, P thẳng hàng.

Vậy M, N, P thẳng hàng.

-- Mod Toán 11 HỌC247